ВЫВОДЫ 1 ПРЕДМЕТОМ науки о строении вещества являются

ВЫВОДЫ 1) ПРЕДМЕТОМ науки о строении вещества являются способы описания реальных объектов посредством сопоставления каждому из них некоторой структурной модели (или совокупности таких моделей) и установление взаимосвязей между свойствами структуры, свойствами частиц и свойствами взаимодействий, 2) МЕТОДОМ науки о строении вещества является конструирование структурных моделей различных типов.

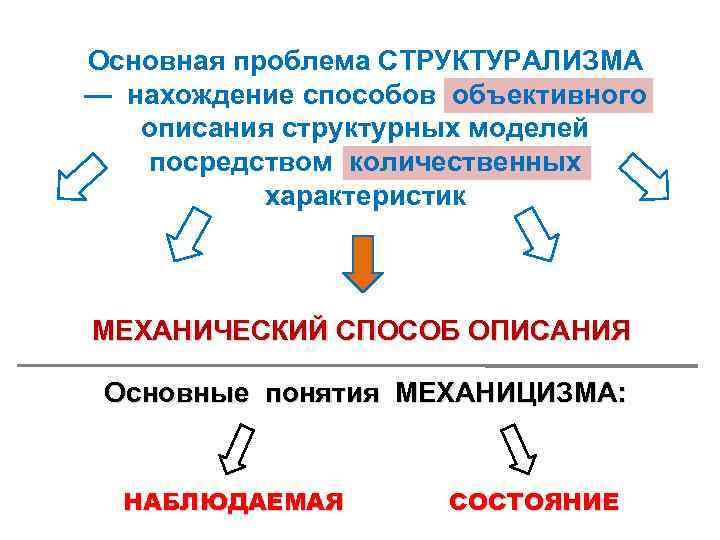Основная проблема СТРУКТУРАЛИЗМА — нахождение способов объективного описания структурных моделей посредством количественных характеристик МЕХАНИЧЕСКИЙ СПОСОБ ОПИСАНИЯ Основные понятия МЕХАНИЦИЗМА: НАБЛЮДАЕМАЯ СОСТОЯНИЕ

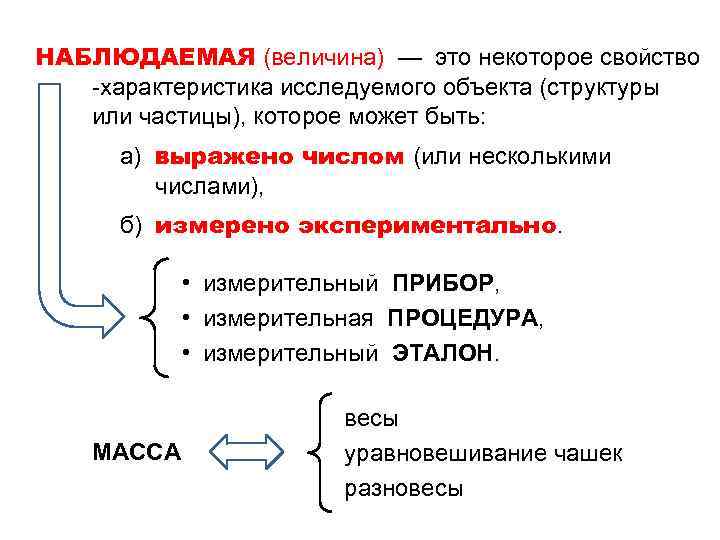НАБЛЮДАЕМАЯ (величина) — это некоторое свойство -характеристика исследуемого объекта (структуры или частицы), которое может быть: а) выражено числом (или несколькими числами), б) измерено экспериментально. • измерительный ПРИБОР, • измерительная ПРОЦЕДУРА, • измерительный ЭТАЛОН. МАССА весы уравновешивание чашек разновесы

Измерительная процедура — сравнение с эталоном: Ах А = —— Аэт А — числовое значение наблюдаемой А, выраженное относительно выбранного эталона: r = 5 [м]; m = 5 [кг]; НАБЛЮДАЕМАЯ Масса = М (весы) E = 5 [Дж]; t = 5 [с] и т. д. ЧИСЛОВОЕ ЗНАЧЕНИЕ М = 5 [кг]

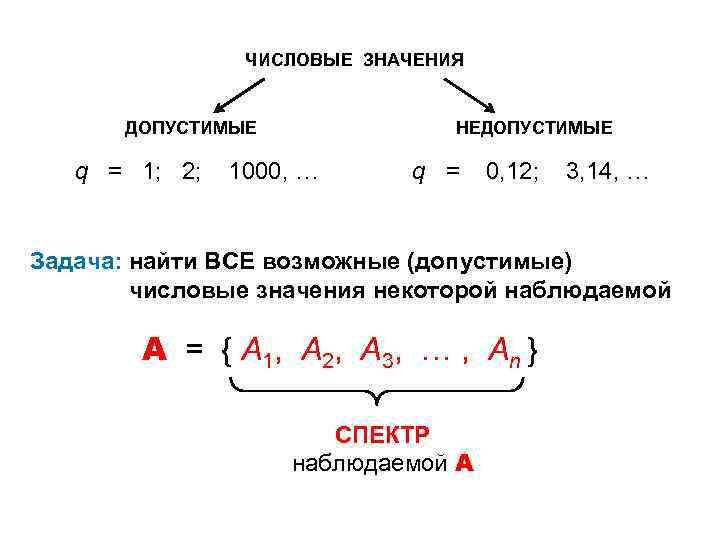ЧИСЛОВЫЕ ЗНАЧЕНИЯ ДОПУСТИМЫЕ q = 1; 2; НЕДОПУСТИМЫЕ 1000, … q = 0, 12; 3, 14, … Задача: найти ВСЕ возможные (допустимые) числовые значения некоторой наблюдаемой A = { A 1, A 2, A 3, … , A n } СПЕКТР наблюдаемой А

Типы спектров ДИСКРЕТНЫЕ Пример: электрический заряд Q = { e, 2 e, 3 e, … , ne } НЕПРЕРЫВНЫЕ (сплошные) Пример: расстояние между двумя частицами R = { 0 — } СМЕШАННЫЕ (дискретно-непрерывные) Пример: энергия электрона в атоме — ниже энергии ионизации ( E < Е* ) спектр дискретный, а выше энергии ионизации ( E > Е* ) спектр непрерывный. ОГРАНИЧЕННЫЕ (координата частицы в ящике) и НЕОГРАНИЧЕННЫЕ (координата свободной частицы) КОНЕЧНЫЕ (проекция спина — два допустимых значения) и БЕСКОНЕЧНЫЕ (координата частицы)

Типы наблюдаемых ОПЕРАЦИОННЫЕ наблюдаемые всегда измеряются непосредственно с помощью приборов: • масса — с помощью весов, • длина — с помощью линейки, • время — с помощью часов и т. д. КОНВЕНЦИОНАЛЬНЫЕ наблюдаемые не измеряются непосредственно, их числовые значения вычисляются по специальным формулам на основании результатов измерений: • скорость v = x/ t • импульс р = mv ; • кинетическая энергия T = mv 2/2 или v = dx/dt ; и т. д.

ЛОКАЛЬНАЯ наблюдаемая относится к одной отдельной частице (например, массы атомов в составе молекулы — m 1, m 2, …). ГЛОБАЛЬНАЯ наблюдаемая относится к структуре в целом (например, масса молекулы — M = m 1 + m 2 + …). ВНЕШНЯЯ наблюдаемая характеризует внешнюю среду, а ВНУТРЕННЯЯ — исследуемый объект. ПРОСТАЯ наблюдаемая выражается одним числом: m = 5 кг ; E = 10 Дж СЛОЖНАЯ наблюдаемая выражается несколькими числами: p = (px , py , pz ) Векторный тип Тензорный тип

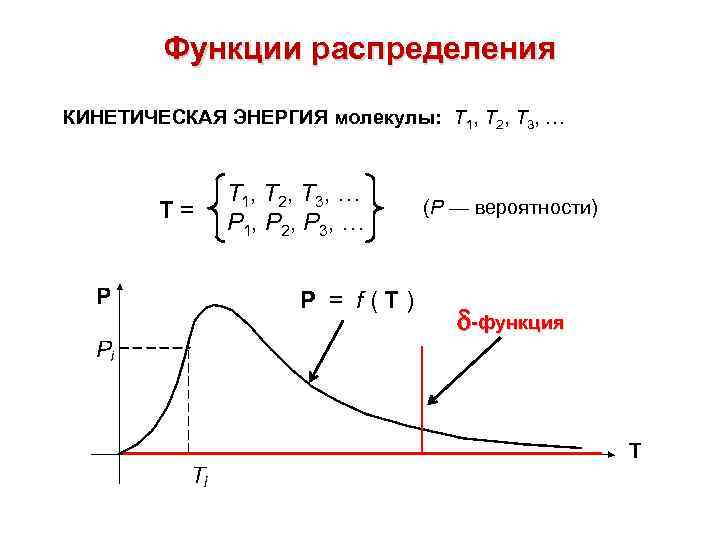Функции распределения КИНЕТИЧЕСКАЯ ЭНЕРГИЯ молекулы: Т 1, Т 2, Т 3, … Т= Т 1, Т 2, Т 3, … Р 1, Р 2, Р 3, … Р = f(T) (Р — вероятности) -функция

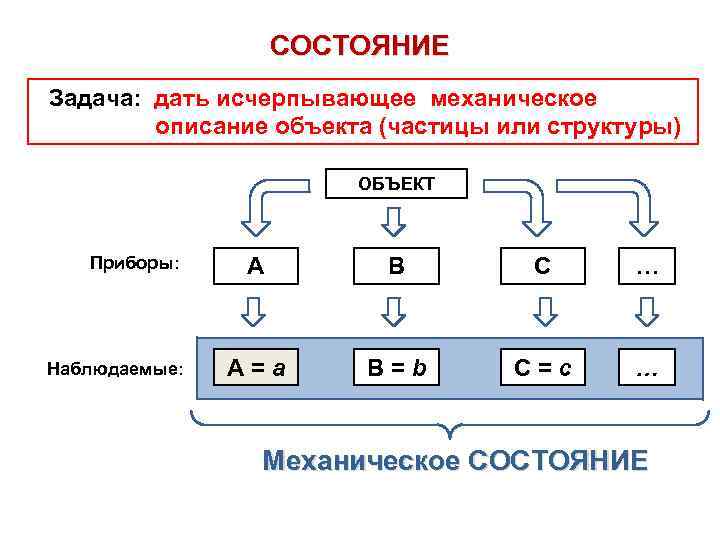СОСТОЯНИЕ Задача: дать исчерпывающее механическое описание объекта (частицы или структуры) ОБЪЕКТ Приборы: Наблюдаемые: А В С … А=а B=b C=c … Механическое СОСТОЯНИЕ

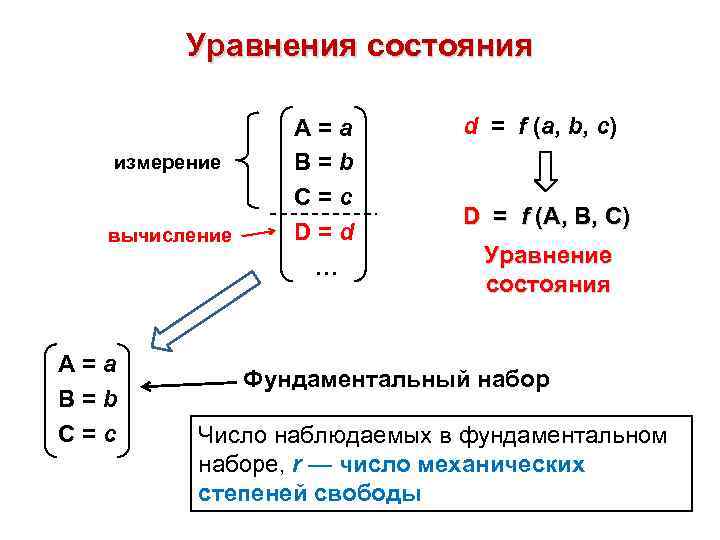Уравнения состояния измерение вычисление А=а B=b C=c D=d … d = f (a, b, c) D = f (A, B, C) Уравнение состояния Фундаментальный набор Число наблюдаемых в фундаментальном наборе, r — число механических степеней свободы

Пример: система, содержащая 1 моль идеального газа Уравнения состояния: P = RT / V; V = RT / P ; T = PV / R Фундаментальные наборы: Число степеней свободы: (P, V); (P, T); (V, T); … r = 2 Условие одновременности Время Энергия Импульс t 1 T 1 p 1 t 2 T 2 p 2 . . Т 1 = р12 / 2 m Т 2 = р22 / 2 m но Т 1 р22 / 2 m Т 2 р12 / 2 m

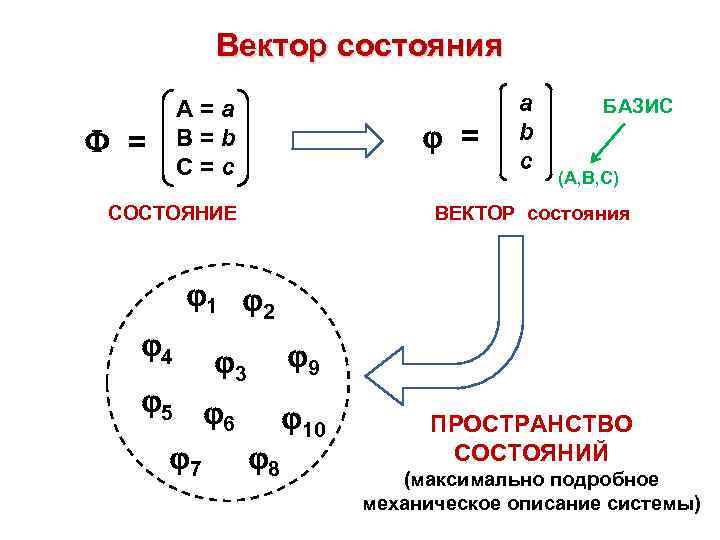Вектор состояния = A=a B=b C=c = a b c БАЗИС (A, B, C) ВЕКТОР состояния СОСТОЯНИЕ 1 2 4 3 9 5 10 6 7 8 ПРОСТРАНСТВО СОСТОЯНИЙ (максимально подробное механическое описание системы)

Принцип суперпозиции 1 = a 1 b 1 c 1 2 = (A, B, C) a 2 b 2 c 2 (A, B, C) 3 = 1 + 2 = = a 1 b 1 c 1 + a 2 b 2 c 2 = a 1 + a 2 b 1 + b 2 c 1 + c 2 = a 3 b 3 c 3

Примеры пространств состояний: • Конфигурационное пространство (3 -х мерное) с координатными осями x, y, z (если имеется N частиц, то размерность равна 3 N); • Галилеево пространство (4 -х мерное), в котором к пространственным осям добавлена временна я — x, y, z, t; • Фазовое пространство (6 -и мерное), в котором кроме трех пространственных осей имеются еще три оси для скоростей или импульсов — x, y, z, vx, vy, vz (если имеется N частиц, то размерность равна 6 N); • Гильбертово пространство квантовой механики (бесконечномерное), где в качестве координатных осей служат некоторые специальные состояния, например, стационарные; • Пространство составов (с переменной размерностью), в котором координатным осям соответствуют чистые химические вещества, а векторам — смеси; • Элементное пространство (с переменной размерностью), в котором координатным осям соответствуют химические элементы, а векторам — химические соединения.

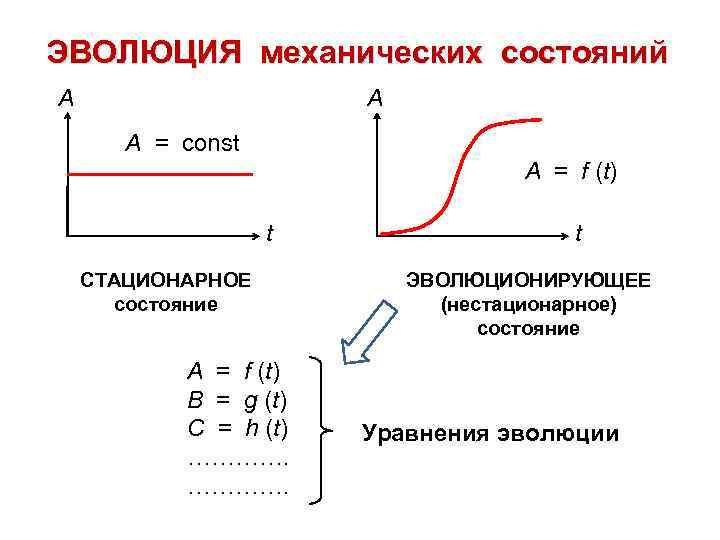ЭВОЛЮЦИЯ механических состояний A A A = const A = f (t) t СТАЦИОНАРНОЕ состояние A = f (t) B = g (t) C = h (t) …………. t ЭВОЛЮЦИОНИРУЮЩЕЕ (нестационарное) состояние Уравнения эволюции

Примеры уравнений эволюции Ньютона: Лагранжа: L=T–U функция Лагранжа H=T+U Гамильтона: функция Гамильтона

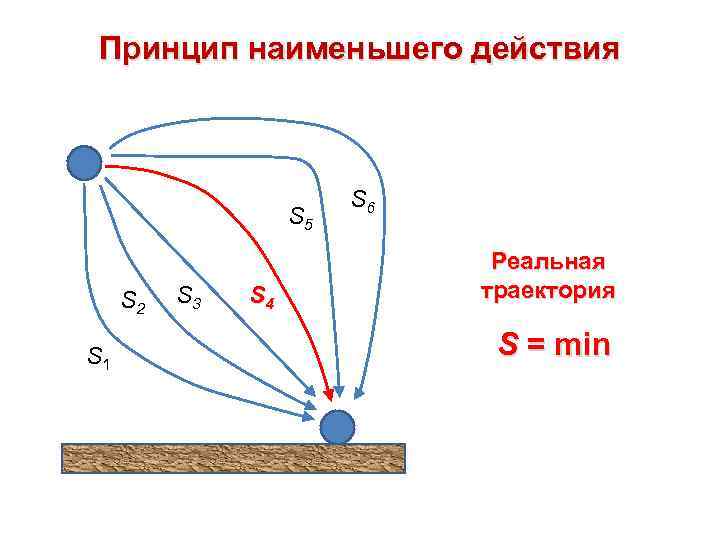Принцип наименьшего действия S 5 S 2 S 1 S 3 S 4 S 6 Реальная траектория S = min

Принцип суперпозиции Любой сложный процесс эволюции (Э) может быть представлен в виде суперпозиции некоторых элементарных процессов (Э 1, Э 2, …), описание которых известно и отличается особенной простотой: Э = С 1 Э 1 + С 2 Э 2 +. . . Примеры элементарных процессов: • трансляция (равномерное движение по прямой), • вращение (равномерное движение по окружности), • гармоническое колебание и др. Произвольная трансляция: Т = Tx + T y + T z Произвольное вращение: R = Rx + R y + R z Движение по спирали: S = Т + R

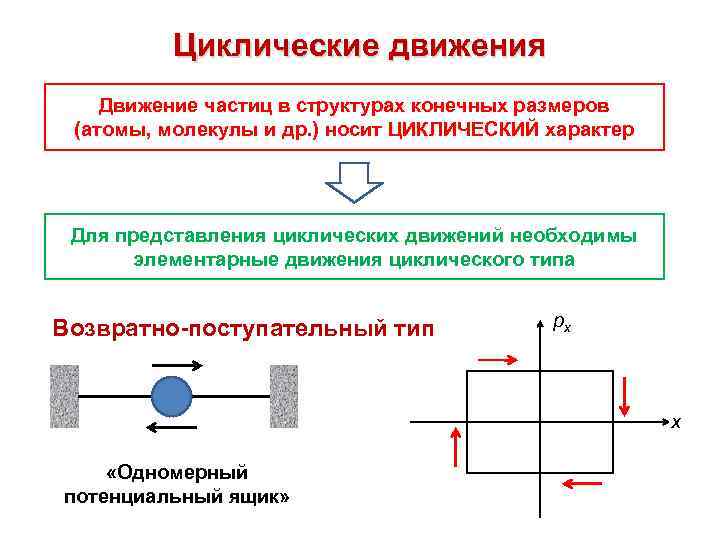Циклические движения Движение частиц в структурах конечных размеров (атомы, молекулы и др. ) носит ЦИКЛИЧЕСКИЙ характер Для представления циклических движений необходимы элементарные движения циклического типа Возвратно-поступательный тип рх х «Одномерный потенциальный ящик»

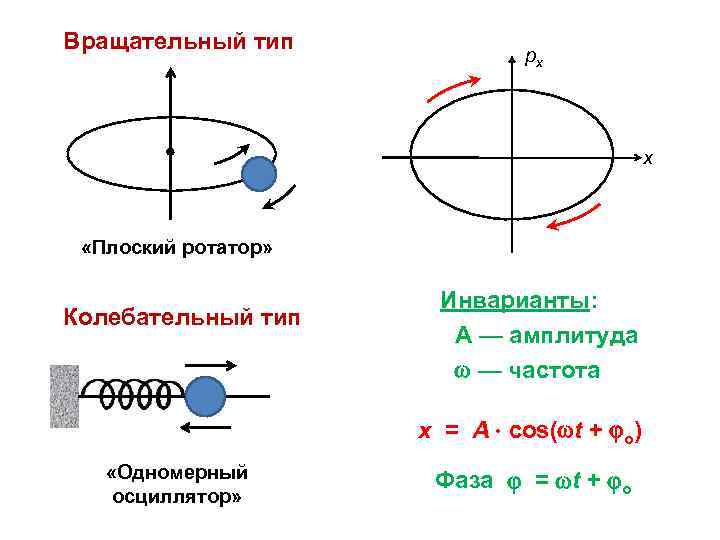Вращательный тип рх х «Плоский ротатор» Колебательный тип Инварианты: А — амплитуда — частота х = A cos( t + o) «Одномерный осциллятор» Фаза = t + o

Адиабатический инвариант медленное изменение размера устройства изменение энергии Е (импульса) и частоты Е / = I = const — адиабатический инвариант Одномерный ПЯ размера L L → L' = L/2 v → v' = 2 v ' ~ v'/L' ~ (2 v)/(L/2) = 4 E' ~ (v' )2 ~ (2 v)2 = 4 E

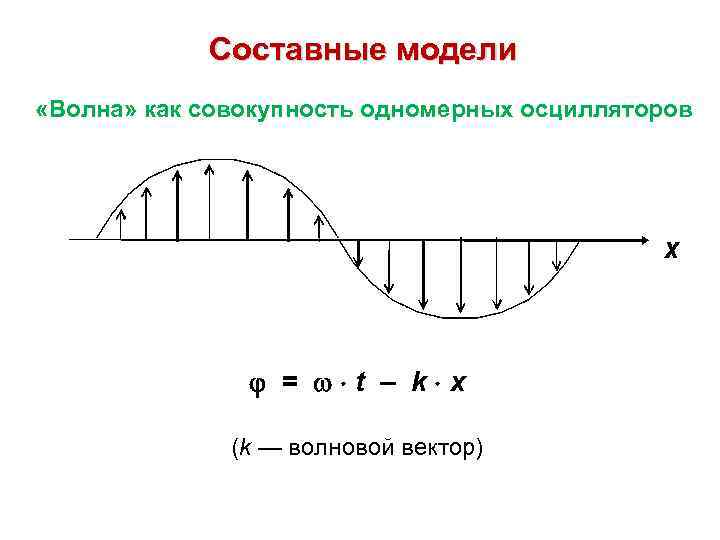Составные модели «Волна» как совокупность одномерных осцилляторов = t – k x (k — волновой вектор)

ВЗАИМОДЕЙСТВИЯ в механическом способе описания Сила, Fq Потенциальная энергия, U d. U Fq = – —— dq U = Fqdq Принцип суперпозиции F = C 1 F 1 + C 2 F 2 + … U = C 1 U 1 + C 2 U 2 + …

Фундаментальные (базисные) взаимодействия ЦВЕТОВЫЕ, действующие между частицами, обладающими т. н. "цветовым зарядом" ("цветом") ЭЛЕКТРОМАГНИТНЫЕ, действующие между частицами, обладающими "электрическим зарядом" ГРАВИТАЦИОННЫЕ, действующие между частицами, обладающими "гравитационным зарядом" ("массой")

Особенности фундаментальных сил ДАЛЬНОДЕЙСТВИЕ: ФС действуют на любых расстояниях, хотя их величина зависит от расстояния между взаимодействующими частицами. НЕНАСЫЩАЕМОСТЬ: с одной выделенной частицей посредством ФС могут взаимодействовать любое число других частиц. При этом величина ФС для данной пары частиц не зависит от наличия или отсутствия других частиц. ИЗОТРОПНОСТЬ: величина ФС не зависит от взаимной ориентации частиц в пространстве, а определяется только расстоянием между ними.

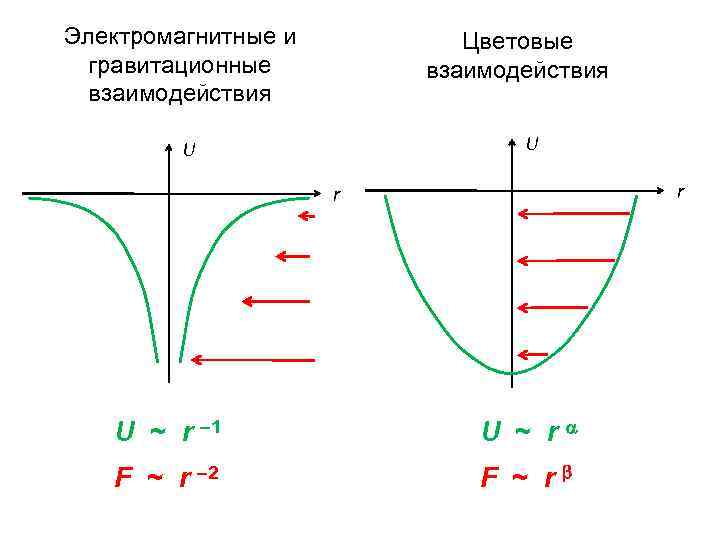Электромагнитные и гравитационные взаимодействия Цветовые взаимодействия U U r r U ~ r – 1 U ~ r F ~ r – 2 F ~ r

Динамический характер взаимодействий Электромагнитные взаимодействия двух точечных электрических зарядов F = FЭ + FМ + FЭМ Зависит только от расстояния КУЛОНОВСКОЕ взаимодействие Зависит от расстояния и скорости МАГНИТНОЕ взаимодействие Зависит от расстояния и ускорения ФОТОННОЕ взаимодействие

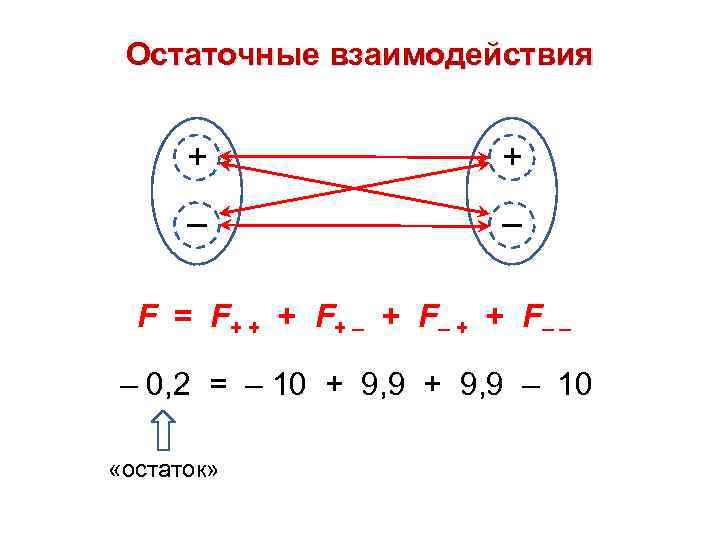Остаточные взаимодействия + + – – F = F+ + + F+ – + F– + + F– – – 0, 2 = – 10 + 9, 9 – 10 «остаток»

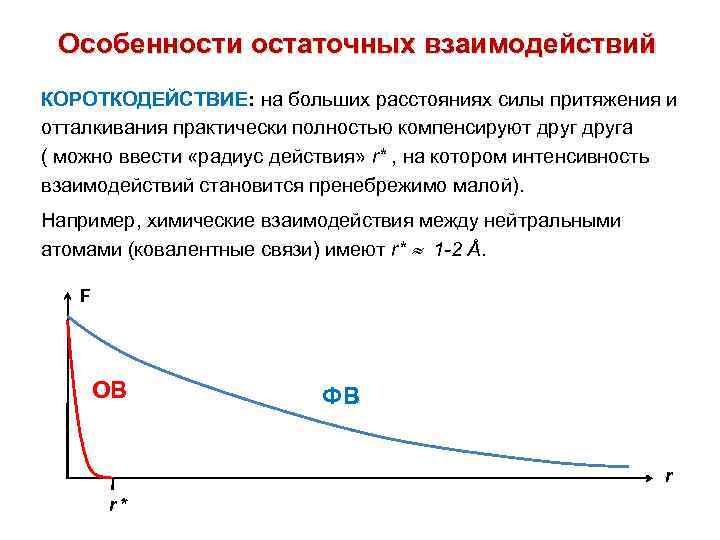Особенности остаточных взаимодействий КОРОТКОДЕЙСТВИЕ: на больших расстояниях силы притяжения и отталкивания практически полностью компенсируют друга ( можно ввести «радиус действия» r* , на котором интенсивность взаимодействий становится пренебрежимо малой). Например, химические взаимодействия между нейтральными атомами (ковалентные связи) имеют r* 1 -2 Å. F ОВ ФВ r r*

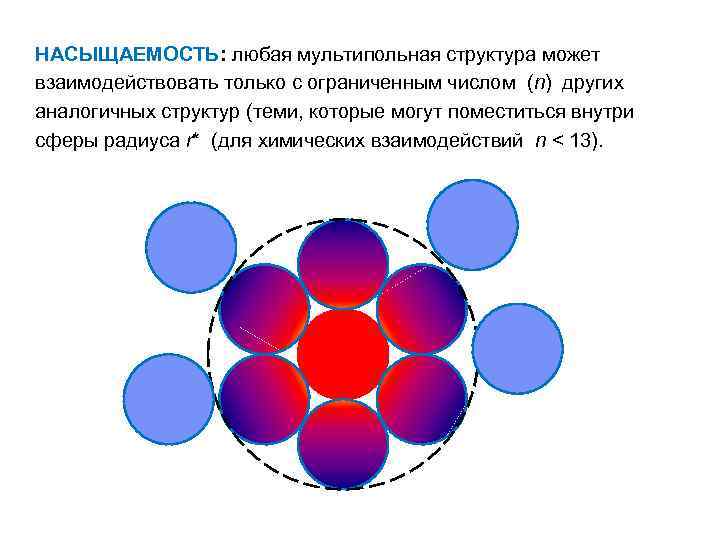НАСЫЩАЕМОСТЬ: любая мультипольная структура может взаимодействовать только с ограниченным числом (n) других аналогичных структур (теми, которые могут поместиться внутри сферы радиуса r* (для химических взаимодействий n < 13).

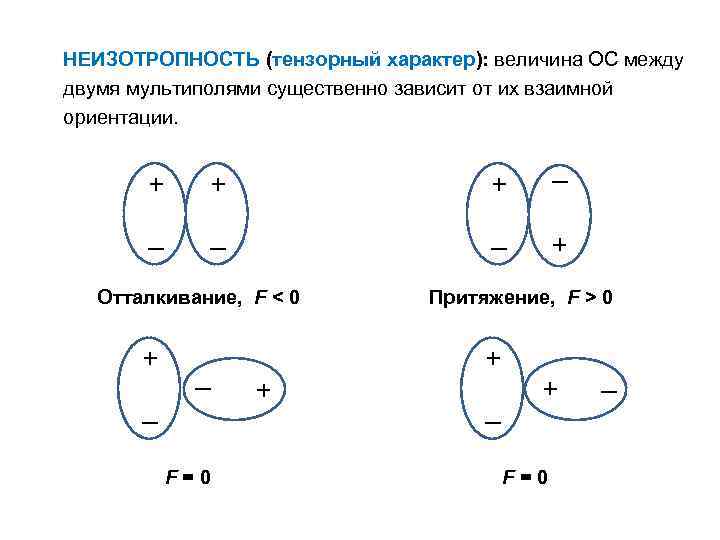НЕИЗОТРОПНОСТЬ (тензорный характер): величина ОС между двумя мультиполями существенно зависит от их взаимной ориентации. + + + – – + Отталкивание, F < 0 – F=0 + – + + + Притяжение, F > 0 – F=0 –

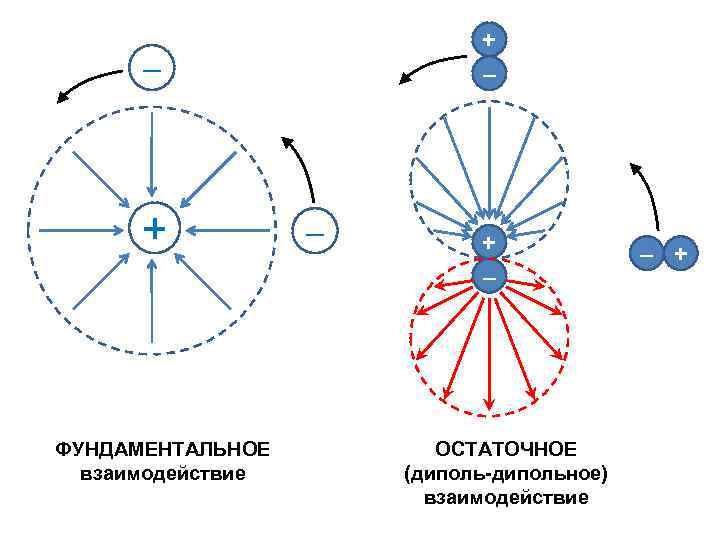+ – – + ФУНДАМЕНТАЛЬНОЕ взаимодействие – + – ОСТАТОЧНОЕ (диполь-дипольное) взаимодействие – +

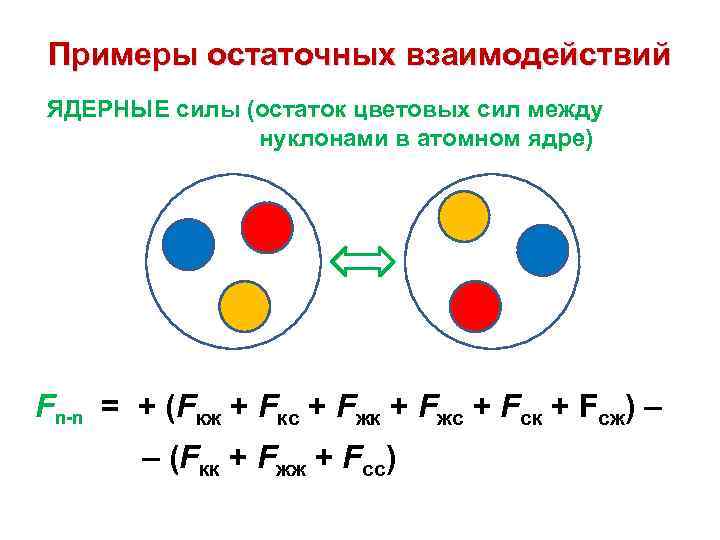Примеры остаточных взаимодействий ЯДЕРНЫЕ силы (остаток цветовых сил между нуклонами в атомном ядре) Fn-n = + (Fкж + Fкс + Fжк + Fжс + Fск + Fсж) – – (Fкк + Fжж + Fсс)

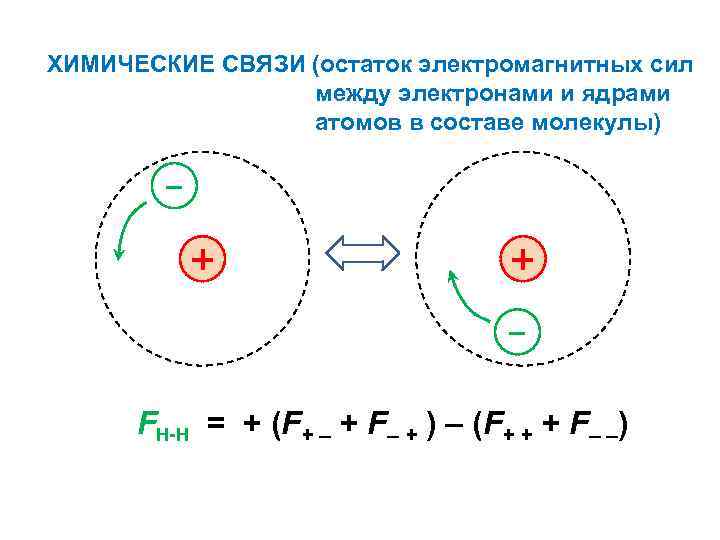ХИМИЧЕСКИЕ СВЯЗИ (остаток электромагнитных сил между электронами и ядрами атомов в составе молекулы) – + + – FН-Н = + (F+ – + F– + ) – (F+ + + F– –)

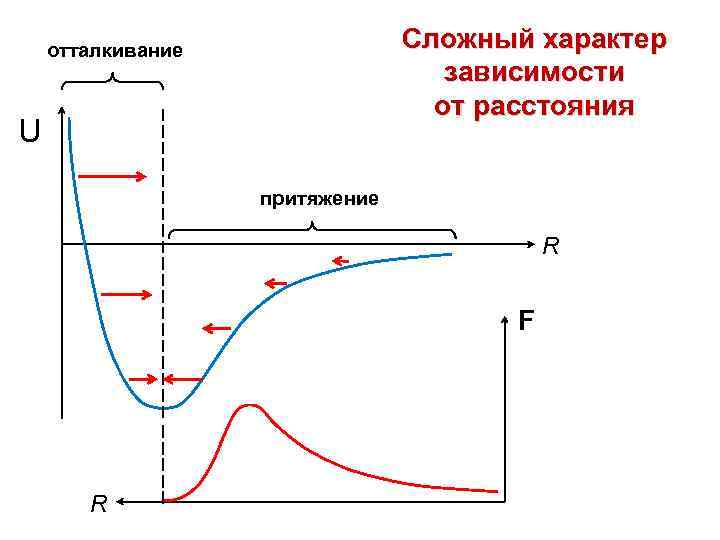Сложный характер зависимости от расстояния отталкивание U притяжение R F R

Дополнительные примеры остаточных электромагнитных взаимодействий • Ван-дер-Ваальсовы силы, • КАПИЛЛЯРНЫЕ силы • АДГЕЗИОННЫЕ силы • Силы ТРЕНИЯ

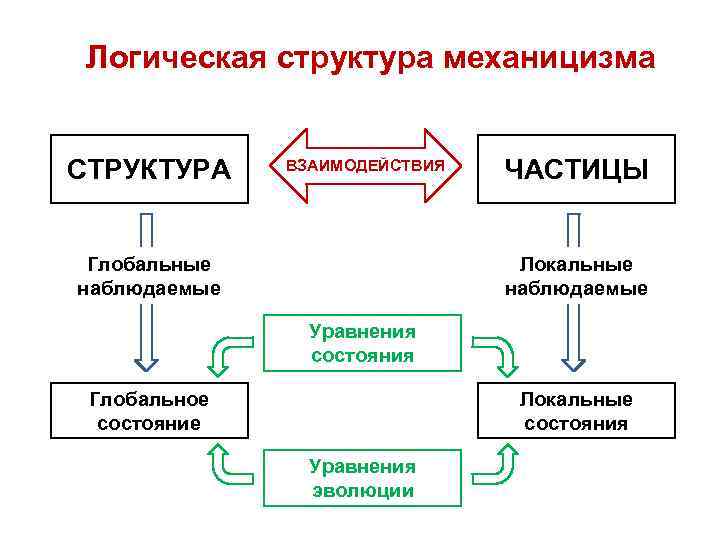Логическая структура механицизма СТРУКТУРА ВЗАИМОДЕЙСТВИЯ Глобальные наблюдаемые ЧАСТИЦЫ Локальные наблюдаемые Уравнения состояния Глобальное состояние Локальные состояния Уравнения эволюции

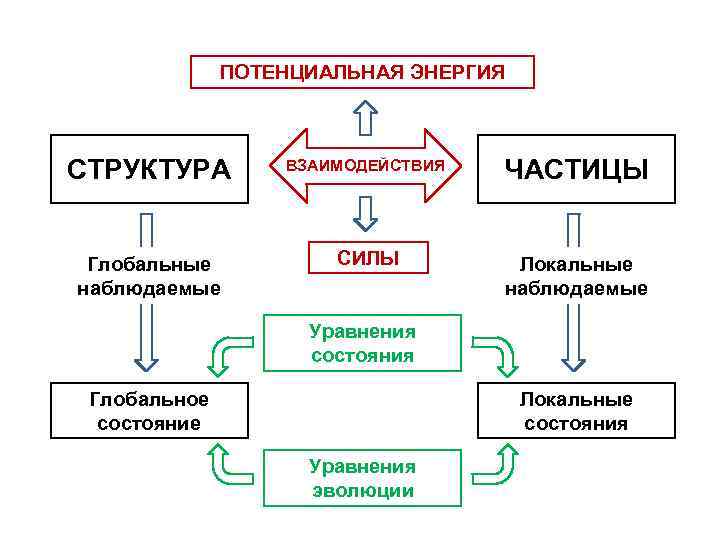ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ СТРУКТУРА ВЗАИМОДЕЙСТВИЯ ЧАСТИЦЫ Глобальные наблюдаемые СИЛЫ Локальные наблюдаемые Уравнения состояния Глобальное состояние Локальные состояния Уравнения эволюции

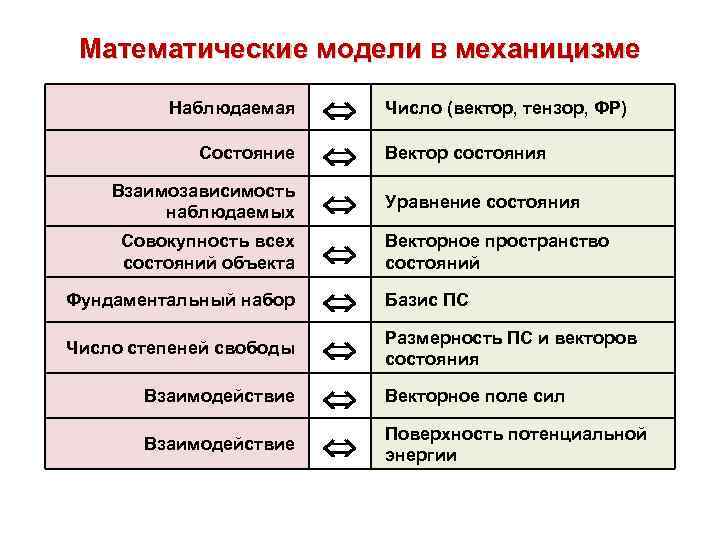Математические модели в механицизме Состояние Взаимозависимость наблюдаемых Уравнение состояния Совокупность всех состояний объекта Векторное пространство состояний Фундаментальный набор Базис ПС Число степеней свободы Размерность ПС и векторов состояния Взаимодействие Векторное поле сил Поверхность потенциальной энергии Наблюдаемая Взаимодействие Число (вектор, тензор, ФР) Вектор состояния