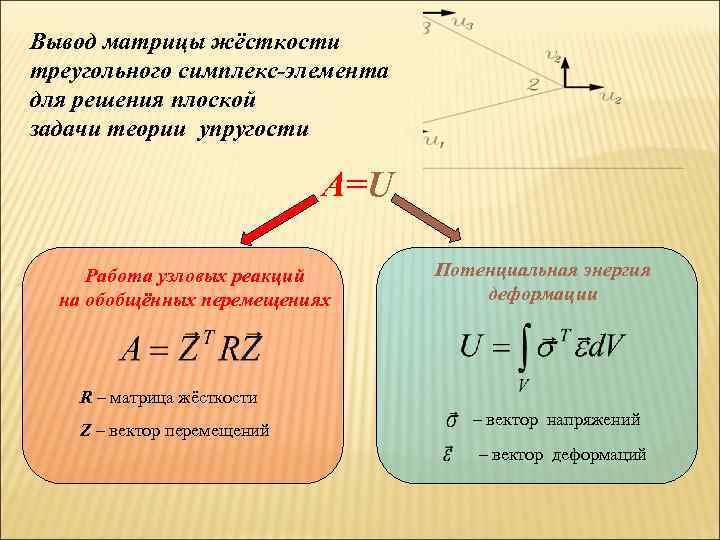
Вывод матрицы жёсткости треугольного симплекс-элемента для решения плоской

Вывод матрицы жёсткости треугольного симплекс-элемента для решения плоской задачи теории упругости A=U Работа узловых реакций на обобщённых перемещениях Потенциальная энергия деформации R – матрица жёсткости Z – вектор перемещений – вектор напряжений – вектор деформаций

Потенциальная энергия деформации: Вектор напряжений - толщина пластины Вектор деформаций Уравнения Коши D – матрица обобщённого закона Гука Связь между перемещениями и деформациями

Поле перемещений для треугольного симплекс-элемента n 1(xy)=[(y-y 2)x 32 - (x-x 2)y 32]/(2 F) n 2(xy)=[(y-y 3)x 13 - (x-x 3)y 13]/(2 F) F – площадь треугольника F=[(y 1 -y 2)(x 3 -x 2) - (x 1 -x 2)(y 3 -y 2)]/2 n 3(xy)=[(y-y 1)x 21 - (x-x 1)y 21]/(2 F)

Построение матрицы деформаций [В]

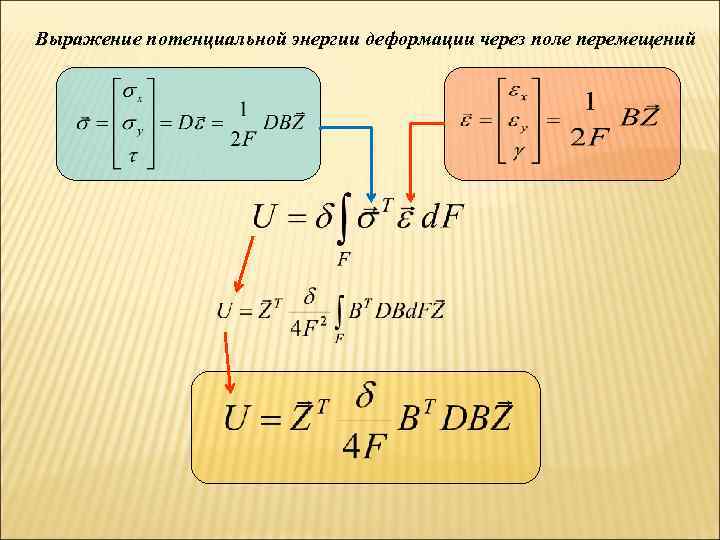Выражение потенциальной энергии деформации через поле перемещений

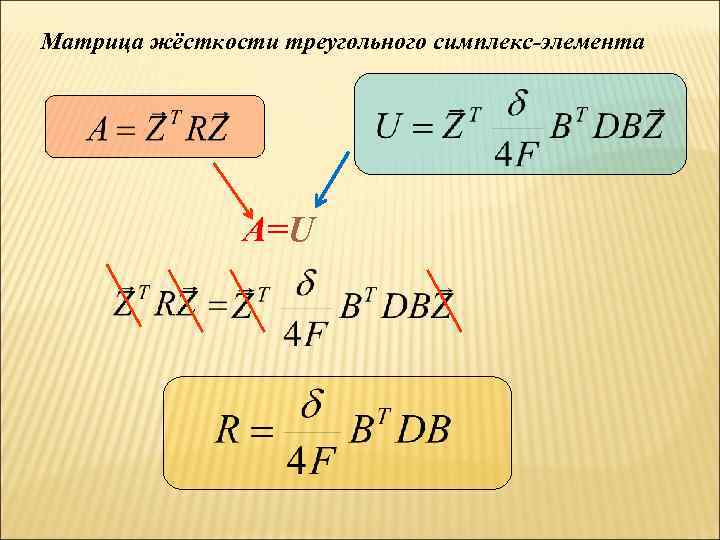Матрица жёсткости треугольного симплекс-элемента A=U