«Высшее назначение математики состоит в том, чтобы

Зарегистрируйтесь, чтобы просмотреть полный документ!

«Высшее назначение математики состоит в том, чтобы находить скрытый порядок в хаосе, который нас окружает. » Н. Винер у у = х2 +2 у = х2 +6 х +9 у = х2 у = (х +3) 2 2 1 -3 0 1 х

Функции и их графики Вид функции Название графика Свойства у у = кх + в линейная Обратная гипербола пропорциональность у= 0 х + х прямая + у у у = а х2 + вх +с у=х у= 3 квадратичная кубическая парабола ветвь у параболы 0 у х 0 х + +

Свойства и графики тригонометрических функций Вид функции Название графика Свойства у = sin х синус ? + ? у = cos х косинус ? + ? у = tg х тангенс ? ? у = сtg х котангенс ? ?

Свойства функций • Область определения функции • Область значения функции • Периодичность • Четность, нечетность • Нули функции • Промежутки знакопостоянства • Промежутки монотонности • Наибольшее (наименьшее) значение функции

Утверждения для точек числовой окружности у I. Определение. sin t = y Синусом числа t называется ордината точки М. М у х 0 -у 3 -х II. Утверждение для точек числовой окружности: М ( t ) = М ( t + 2 n ), n 0 х 2 III. sin (x +2 n) = sin х, n z f (х +Т) = f (х –Т) = f (х) Функция периодическая IV. sin (-х) = - sin х f (-х) = - f (х) Функция нечетная z

Область определения Область значения функции у 1 D(у)=(- ; + Е(у)= [-1; 1] ) 0 х 0 -1 2π

Наибольшее и наименьшее значение функции. Нули функции. Промежутки знакопостоянства. у π/2 у=0 1 π -π 0 0 х при x = 0 + πn, n унаиб. = 1 при х = z +2 n, n Z 2π -1 3π/2 - π/2 y>0 y<0 унаим. = -1 при х = - + 2 n, n Z при 0 <x< π при х (2πn; π+2πn), n z при -π < x < 0 при х (-π + 2πn; 2πn), n z

Промежутки монотонности II х1 х2 у π 2 у2 sin х1 sin х 2 М 2 у1 III х1 х2 π -π I х2 0 sin х 1 sin х 2 х1 х2 sin х 1 sin х2 М 1 х1 0 х IV х1 х2 sin х 1 sin х 2 3 π 2 - π 2 Функция возрастает на - /2 + 2 n; /2 + 2 n , Z n Функция убывает на /2 + 2 n; 3 /2 + 2 n , n Z

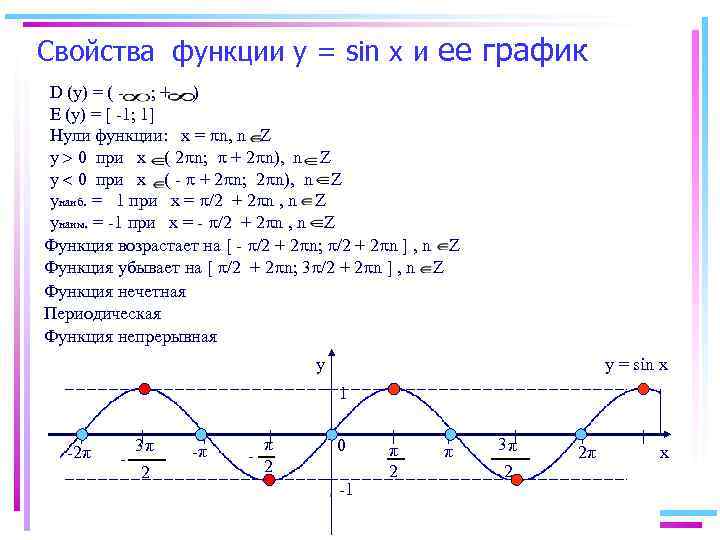
Свойства функции у = sin х и ее график D (у) = ( ; + ) Е (у) = -1; 1 Нули функции: х = n, n Z у 0 при х ( 2 n; + 2 n), n Z у 0 при х ( - + 2 n; 2 n), n Z унаиб. = 1 при х = /2 + 2 n , n Z унаим. = -1 при х = - /2 + 2 n , n Z Функция возрастает на - /2 + 2 n; /2 + 2 n , n Z Функция убывает на /2 + 2 n; 3 /2 + 2 n , n Z Функция нечетная Периодическая Функция непрерывная y y = sin x 1 -2π 3π 2 -π - π 2 0 -1 π 2 π 3π 2 2π x

Синусоида – график функции у = sin х y 3 2 y = sin x 1 -2π - 3π 2 -π - π 2 0 -1 π 2 π 3π 2 2π x

Человека, умеющего наблюдать и анализировать, обмануть просто невозможно. Его выводы будут безошибочны, как теорема Пифагора. А. Конан Дойл

Синусоида – график функции у = sin х График функции y = соs x y 2 y = sin ( x + /2) 1 -2π - 3π 2 -π - π 2 0 -1 π 2 π 3π 2 2π x

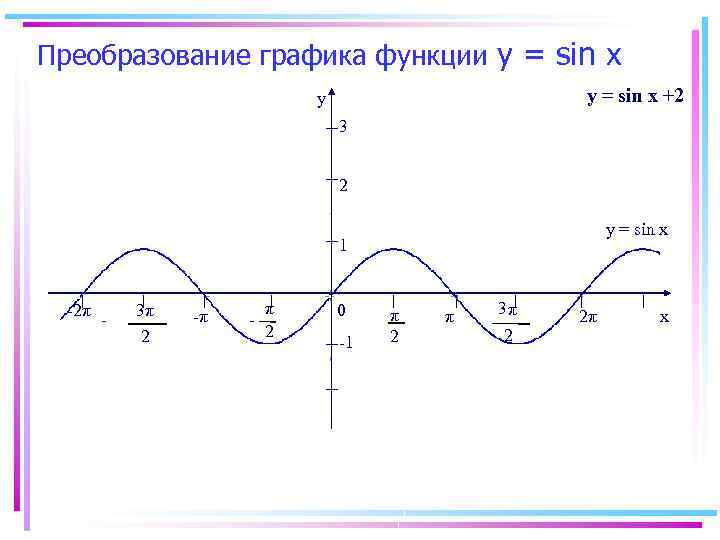
Преобразование графика функции y = sin x +2 y 3 2 y = sin x 1 -2π - 3π 2 -π - π 2 0 -1 π 2 π 3π 2 2π x

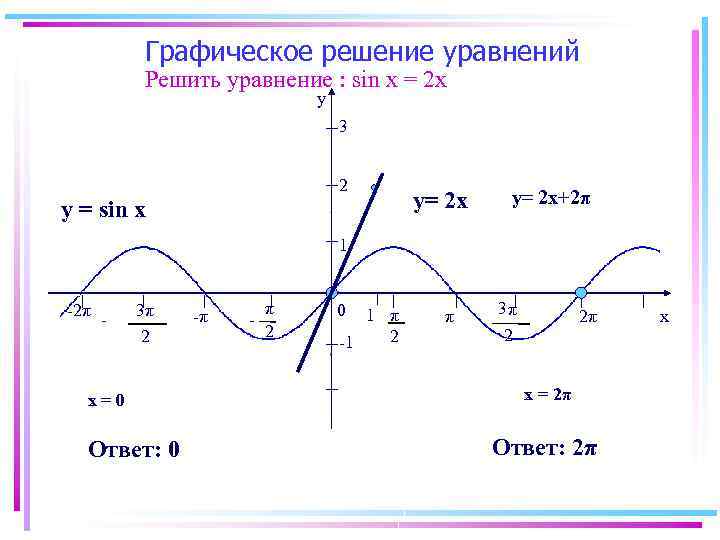
Графическое решение уравнений Решить уравнение : sin x = 2 х y 3 2 y = sin x у= 2 х+2π 1 -2π - 3π 2 х=0 Ответ: 0 -π - π 2 0 1 π 2 -1 π 3π 2π 2 х = 2π Ответ: 2π x

Синусоида – график функции у = sin х y 3 2 y = sin x 1 -2π - 3π 2 -π - π 2 0 -1 π 2 π 3π 2 2π x

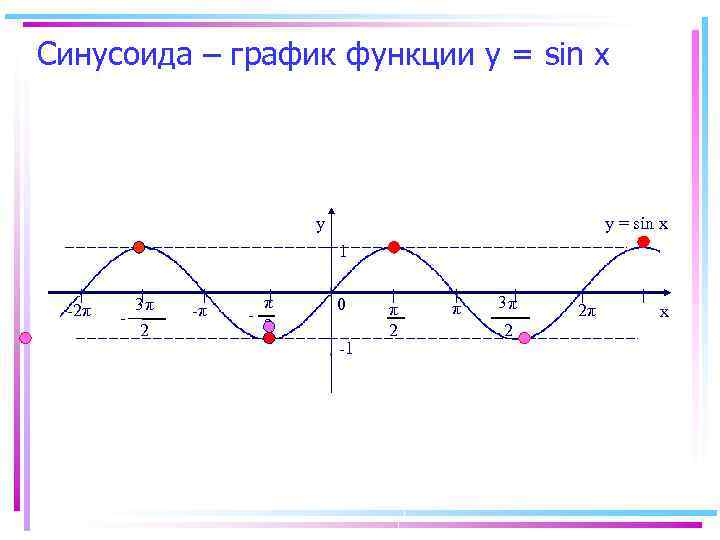
Синусоида – график функции у = sin х y y = sin x 1 -2π - 3π 2 -π - π 2 0 -1 π 2 π 3π 2 2π x

Скачать презентацию «Высшее назначение математики состоит в том, чтобы

свойства и график ф-ции y=sinx.ppt

Количество слайдов: 18