Скачать презентацию ВЫСШАЯ ШКОЛА ПРИВАТИЗАЦИИ И ПРЕДПРИНИМАТЕЛЬСТВА Математическая статистика МЕТОДЫ Скачать презентацию ВЫСШАЯ ШКОЛА ПРИВАТИЗАЦИИ И ПРЕДПРИНИМАТЕЛЬСТВА Математическая статистика МЕТОДЫ

мат_стат_лекция_5(сл).ppt

  • Количество слайдов: 48

ВЫСШАЯ ШКОЛА ПРИВАТИЗАЦИИ И ПРЕДПРИНИМАТЕЛЬСТВА Математическая статистика. МЕТОДЫ РАСЧЕТА СВОДНЫХ ХАРАКТЕРИСТИК ВЫБОРКИ Автор: доцент ВЫСШАЯ ШКОЛА ПРИВАТИЗАЦИИ И ПРЕДПРИНИМАТЕЛЬСТВА Математическая статистика. МЕТОДЫ РАСЧЕТА СВОДНЫХ ХАРАКТЕРИСТИК ВЫБОРКИ Автор: доцент кафедры информатики и математики Грязнов Сергей Александрович

Условные варианты Предположим, что варианты выборки расположены в возрастающем порядке, т. е. в виде Условные варианты Предположим, что варианты выборки расположены в возрастающем порядке, т. е. в виде вариационного ряда.

Условные варианты Равноотстоящими называют варианты, которые образуют арифметическую прогрессию с разностью h. Условные варианты Равноотстоящими называют варианты, которые образуют арифметическую прогрессию с разностью h.

Условные варианты Условными называют варианты, определяемые равенством: где С—ложный нуль (новое начало отсчета); h—шаг, Условные варианты Условными называют варианты, определяемые равенством: где С—ложный нуль (новое начало отсчета); h—шаг, т. е. разность между любыми двумя соседними первоначальными вариантами (новая единица масштаба).

Условные варианты Упрощенные методы расчета сводных характеристик выборки основаны на замене первоначальных вариант условными. Условные варианты Упрощенные методы расчета сводных характеристик выборки основаны на замене первоначальных вариант условными.

Условные варианты. Замечание 1 В качестве ложного нуля можно принять любую варианту. Максимальная простота Условные варианты. Замечание 1 В качестве ложного нуля можно принять любую варианту. Максимальная простота вычислений достигается, если выбрать в качестве ложного нуля варианту, которая расположена примерно в середине вариационного ряда (часто такая варианта имеет наибольшую частоту).

Условные варианты. Замечание 2 Варианте, которая принята в качестве ложного нуля, соответствует условная варианта, Условные варианты. Замечание 2 Варианте, которая принята в качестве ложного нуля, соответствует условная варианта, равная нулю.

Условные варианты. Пример. Найти условные варианты статистического распределения: Условные варианты. Пример. Найти условные варианты статистического распределения:

Условные варианты. Решение Выберем в качестве ложного нуля варианту 33, 6 (эта варианта расположена Условные варианты. Решение Выберем в качестве ложного нуля варианту 33, 6 (эта варианта расположена в середине вариационного ряда). Найдем шаг:

Условные варианты. Решение Найдем условную варианту: Аналогично получим: и 2= -1, и 3 = Условные варианты. Решение Найдем условную варианту: Аналогично получим: и 2= -1, и 3 = 0, и 4 =1, и 5=2. Мы видим, что условные варианты – небольшие целые числа. Разумеется, оперировать с ними проще, чем с первоначальными вариантами.

Обычные, начальные и центральные эмпирические моменты Для вычисления сводных характеристик выборки удобно пользоваться эмпирическими Обычные, начальные и центральные эмпирические моменты Для вычисления сводных характеристик выборки удобно пользоваться эмпирическими моментами. В отличии от теоретических эмпирические вычисляют по данным наблюдений.

Обычные, начальные и центральные эмпирические моменты Обычным эмпирическим моментом порядка k называют среднее значение Обычные, начальные и центральные эмпирические моменты Обычным эмпирическим моментом порядка k называют среднее значение k-x степеней разностей xi — С:

Обычные, начальные и центральные эмпирические моменты Начальным эмпирическим моментом порядка k называют обычный момент Обычные, начальные и центральные эмпирические моменты Начальным эмпирическим моментом порядка k называют обычный момент порядка k при С = 0

Обычные, начальные и центральные эмпирические моменты В частности, т. е. начальный эмпирический момент первого Обычные, начальные и центральные эмпирические моменты В частности, т. е. начальный эмпирический момент первого порядка равен выборочной средней.

Обычные, начальные и центральные эмпирические моменты Центральным эмпирическим моментом порядка k называют обычный момент Обычные, начальные и центральные эмпирические моменты Центральным эмпирическим моментом порядка k называют обычный момент порядка k при

Обычные, начальные и центральные эмпирические моменты В частности, т. е. центральный эмпирический момент второго Обычные, начальные и центральные эмпирические моменты В частности, т. е. центральный эмпирический момент второго порядка равен выборочной дисперсии.

Обычные, начальные и центральные эмпирические моменты Легко выразить центральные моменты через обычные: Обычные, начальные и центральные эмпирические моменты Легко выразить центральные моменты через обычные:

Условные эмпирические моменты. Отыскание центральных моментов по условным Вычисление центральных моментов требует довольно громоздких Условные эмпирические моменты. Отыскание центральных моментов по условным Вычисление центральных моментов требует довольно громоздких вычислений. Чтобы упростить расчеты, заменяют первоначальные варианты условными.

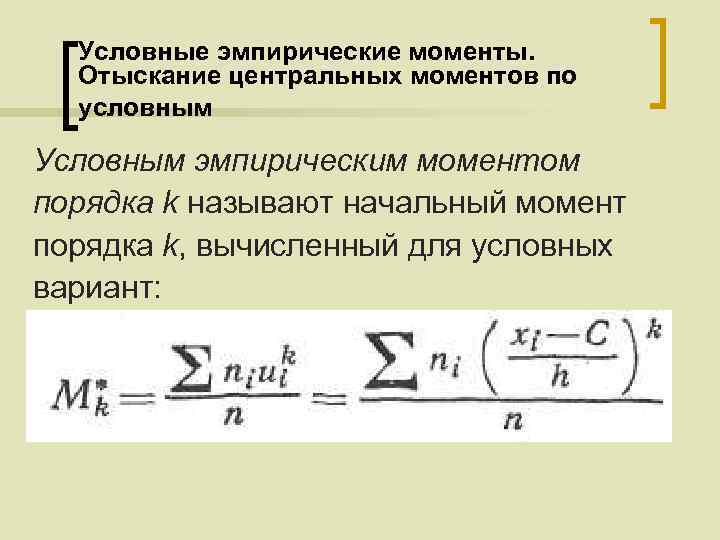Условные эмпирические моменты. Отыскание центральных моментов по условным Условным эмпирическим моментом порядка k называют Условные эмпирические моменты. Отыскание центральных моментов по условным Условным эмпирическим моментом порядка k называют начальный момент порядка k, вычисленный для условных вариант:

Условные эмпирические моменты. Отыскание центральных моментов по условным В частности, Условные эмпирические моменты. Отыскание центральных моментов по условным В частности,

Условные эмпирические моменты. Отыскание центральных моментов по условным Отсюда, Таким образом, для того чтобы Условные эмпирические моменты. Отыскание центральных моментов по условным Отсюда, Таким образом, для того чтобы найти выборочную среднюю, достаточно вычислить условный момент первого порядка, умножить его на h и к результату прибавить ложный нуль С.

Условные эмпирические моменты. Отыскание центральных моментов по условным Выразим обычные моменты через условные: Условные эмпирические моменты. Отыскание центральных моментов по условным Выразим обычные моменты через условные:

Условные эмпирические моменты. Отыскание центральных моментов по условным Отсюда, Таким образом, для того чтобы Условные эмпирические моменты. Отыскание центральных моментов по условным Отсюда, Таким образом, для того чтобы найти обычный момент порядка k, достаточно условный момент того же порядка умножить на hk.

Условные эмпирические моменты. Отыскание центральных моментов по условным Найдя же обычные моменты, легко найти Условные эмпирические моменты. Отыскание центральных моментов по условным Найдя же обычные моменты, легко найти центральные моменты. В итоге получим удобные для вычислений формулы, выражающие центральные моменты через условные:

Условные эмпирические моменты. Отыскание центральных моментов по условным В частности, получим формулу для вычисления Условные эмпирические моменты. Отыскание центральных моментов по условным В частности, получим формулу для вычисления выборочной дисперсии по условным моментам первого и второго порядков

Метод произведений для вычисления выборочных средней и дисперсии Метод произведений дает удобный способ вычисления Метод произведений для вычисления выборочных средней и дисперсии Метод произведений дает удобный способ вычисления условных моментов различных порядков вариационного ряда с равноотстоящими вариантами. Зная же условные моменты, нетрудно найти интересующие нас начальные и центральные эмпирические моменты.

Метод произведений для вычисления выборочных средней и дисперсии В частности, методом произведений удобно вычислять Метод произведений для вычисления выборочных средней и дисперсии В частности, методом произведений удобно вычислять выборочную среднюю и выборочную дисперсию. Целесообразно пользоваться расчетной таблицей, которая составляется по следующим правилам:

Метод произведений для вычисления выборочных средней и дисперсии 1) в первый столбец таблицы записывают Метод произведений для вычисления выборочных средней и дисперсии 1) в первый столбец таблицы записывают выборочные (первоначальные) варианты, располагая их в возрастающем порядке;

Метод произведений для вычисления выборочных средней и дисперсии 2) во второй столбец записывают частоты Метод произведений для вычисления выборочных средней и дисперсии 2) во второй столбец записывают частоты вариант; складывают все частоты и их сумму (объем выборки n) помещают в нижнюю клетку столбца;

Метод произведений для вычисления выборочных средней и дисперсии 3) в третий столбец записывают условные Метод произведений для вычисления выборочных средней и дисперсии 3) в третий столбец записывают условные варианты ui = (xi — C)/h, причем в качестве ложного нуля С выбирают варианту, которая расположена примерно в середине вариационного ряда, и полагают h равным разности между любыми двумя соседними вариантами; практически же третий столбец заполняется так: в клетке строки, содержащей выбранный ложный нуль, пишут 0; в клетках над нулем пишут последовательно — 1, — 2, — 3 и т. д. , а под нулем — 1, 2, 3 и т. д. ;

Метод произведений для вычисления выборочных средней и дисперсии 4) умножают частоты на условные варианты Метод произведений для вычисления выборочных средней и дисперсии 4) умножают частоты на условные варианты и записывают их произведения niui в четвертый столбец; сложив все полученные числа, их сумму помещают в нижнюю клетку столбца;

Метод произведений для вычисления выборочных средней и дисперсии 5) умножают частоты на квадраты условных Метод произведений для вычисления выборочных средней и дисперсии 5) умножают частоты на квадраты условных вариант и записывают их произведения niui 2 в пятый столбец; сложив все полученные числа, их сумму помещают в нижнюю клетку столбца;

Метод произведений для вычисления выборочных средней и дисперсии 6) умножают частоты на квадраты условных Метод произведений для вычисления выборочных средней и дисперсии 6) умножают частоты на квадраты условных вариант, увеличенных каждая на единицу, и записывают произведения в шестой контрольный столбец; сложив все полученные числа, их сумму помещают в нижнюю клетку столбца.

Метод произведений для вычисления выборочных средней и дисперсии. Замечание 1. Целесообразно отдельно складывать отрицательные Метод произведений для вычисления выборочных средней и дисперсии. Замечание 1. Целесообразно отдельно складывать отрицательные числа четвертого столбца (их сумму А 1 записывают в клетку строки, содержащей ложный нуль) и отдельно положительные числа (их сумму А 2 записывают в предпоследнюю клетку столбца); тогда

Метод произведений для вычисления выборочных средней и дисперсии. Замечание 2. При вычислении произведений niui Метод произведений для вычисления выборочных средней и дисперсии. Замечание 2. При вычислении произведений niui 2 пятого столбца целесообразно числа niui четвертого столбца умножать на ui.

Метод произведений для вычисления выборочных средней и дисперсии. Замечание 3. Метод произведений для вычисления выборочных средней и дисперсии. Замечание 3.

Метод произведений для вычисления выборочных средней и дисперсии После того как расчетная таблица заполнена Метод произведений для вычисления выборочных средней и дисперсии После того как расчетная таблица заполнена и проверена правильность вычислений, вычисляют условные моменты:

Метод произведений для вычисления выборочных средней и дисперсии Наконец, вычисляют выборочные среднюю и дисперсию: Метод произведений для вычисления выборочных средней и дисперсии Наконец, вычисляют выборочные среднюю и дисперсию:

Метод произведений для вычисления выборочных средней и дисперсии. Пример Найти методом произведений выборочные среднюю Метод произведений для вычисления выборочных средней и дисперсии. Пример Найти методом произведений выборочные среднюю и дисперсию следующего статистического распределения:

Метод произведений для вычисления выборочных средней и дисперсии. Решение. Составим расчетную таблицу, для чего: Метод произведений для вычисления выборочных средней и дисперсии. Решение. Составим расчетную таблицу, для чего: 1) запишем варианты в первый столбец; 2) запишем частоты во второй столбец; сумму частот (100) поместим в нижнюю клетку столбца;

Метод произведений для вычисления выборочных средней и дисперсии. Решение. 3) в качестве ложного нуля Метод произведений для вычисления выборочных средней и дисперсии. Решение. 3) в качестве ложного нуля выберем варианту 11, 0 (эта варианта расположена примерно в середине вариационного ряда); в клетке третьего столбца, которая принадлежит строке, содержащей выбранный ложный нуль, пишем 0; над нулем записываем последовательно — 1, — 2, — 3, — 4, а под нулем — 1, 2, 3, 4, 5;

Метод произведений для вычисления выборочных средней и дисперсии. Решение. 4) произведения частот на условные Метод произведений для вычисления выборочных средней и дисперсии. Решение. 4) произведения частот на условные варианты записываем в четвертый столбец; отдельно находим сумму (— 46) отрицательных и отдельно сумму (103) положительных чисел; сложив эти числа, их сумму (57) помещаем в нижнюю клетку столбца;

Метод произведений для вычисления выборочных средней и дисперсии. Решение. 5) произведения частот на квадраты Метод произведений для вычисления выборочных средней и дисперсии. Решение. 5) произведения частот на квадраты условных вариант запишем в пятый столбец; сумму чисел столбца (383) помещаем в нижнюю клетку столбца;

Метод произведений для вычисления выборочных средней и дисперсии. Решение. 6) произведения частот на квадраты Метод произведений для вычисления выборочных средней и дисперсии. Решение. 6) произведения частот на квадраты условных вариант, увеличенных на единицу, запишем в шестой контрольный столбец; сумму (597) чисел столбца помещаем в нижнюю клетку столбца.

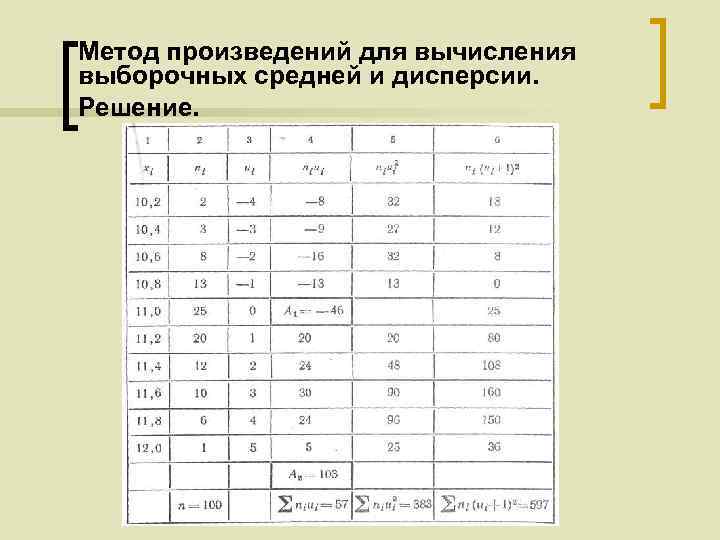
Метод произведений для вычисления выборочных средней и дисперсии. Решение. Метод произведений для вычисления выборочных средней и дисперсии. Решение.

Метод произведений для вычисления выборочных средней и дисперсии. Решение. Вычислим условные моменты первого и Метод произведений для вычисления выборочных средней и дисперсии. Решение. Вычислим условные моменты первого и второго порядков:

Метод произведений для вычисления выборочных средней и дисперсии. Решение. Найдем шаг: Вычислим искомые выборочные Метод произведений для вычисления выборочных средней и дисперсии. Решение. Найдем шаг: Вычислим искомые выборочные среднюю и дисперсию:

ВЫСШАЯ ШКОЛА ПРИВАТИЗАЦИИ И ПРЕДПРИНИМАТЕЛЬСТВА Математическая статистика. МЕТОДЫ РАСЧЕТА СВОДНЫХ ХАРАКТЕРИСТИК ВЫБОРКИ Автор: доцент ВЫСШАЯ ШКОЛА ПРИВАТИЗАЦИИ И ПРЕДПРИНИМАТЕЛЬСТВА Математическая статистика. МЕТОДЫ РАСЧЕТА СВОДНЫХ ХАРАКТЕРИСТИК ВЫБОРКИ Автор: доцент кафедры информатики и математики Грязнов Сергей Александрович