Высшая математика Структура курса (I семестр) -линейная

Высшая математика

Структура курса (I семестр) -линейная алгебра; -векторный анализ; -аналитическая геометрия; -математический анализ; -дифференциальное исчисление функции одной переменной.

Литература Пискунов Н. С. Дифференциальное и интегральное исчисления Щипачев В. С. Высшая математика Минорский В. П. Сборник задач по высшей математике Данко П. В. , Попов А. Г. , Кожевникова Г. Н. Высшая математика в упражнениях и задачах. Т. 1, 2.

Матрицы

Матрица размером m x n: прямоугольная таблица чисел, состоящая из m строк и n столбцов: - элемент матрицы - номер строки - номер столбца

Одностолбцовая матрица (вектор) имеет размер : Однострочная матрица (вектор) имеет размер :

Квадратная матрица : число строк равно числу столбцов Порядок квадратной матрицы: количество ее строк (столбцов) - матрица n-го порядка Главная диагональ квадратной матрицы n-го порядка: совокупность элементов с одинаковыми индексами Побочная диагональ: совокупность элементов, расположенных на второй диагонали

Диагональная матрица: квадратная матрица, все элементы которой, расположенные вне главной диагонали, равны нулю Единичная матрица: диагональная матрица , все диагональные элементы которой равны единице

Нулевая матрица: все элементы ее равны нулю Расширенная матрица: состоит из двух матриц, разделенных чертой

Операции над матрицами Равные матрицы A и B: имеют одинаковый размер и их соответствующие элементы равны : Произведение матрицы A на число матрица B, такая что :

Свойства операции умножения матрицы на число 1. Распределительное : 2. Сочетательное : 3. 4.

Сумма матриц A и B, имеющих одинаковый размер: матрица C, каждый элемент которой равен сумме соответствующих элементов матриц A и B: Свойства операции сложения 1. Переместительное 2. Сочетательное 3. Сумма любой матрицы A и нулевой матрицы того же размера равна матрице A

Разность матриц A и B, имеющих одинаковый размер: матрица D, каждый элемент которой равен сумме соответствующих элементов матриц A и (-1)х. B: Транспонированная матрица: столбцы матрицы А являются строками матрицы

Свойства операции транспонирования матрицы 1. Диагональные элементы при транспонировании остаются на своих местах 2. Доказательство. 3. 4.

Пример.

Произведение матрицы A (m x p) на матрицу B(p x n) : матрица C (m x n), каждый элемент которой равен Свойства операции умножения матриц 1. Сочетательное 2. Распределительное: 3. 4. 5. 6.

7. Перемножение матриц некоммутативно: -произведение матрицы A на матрицу B справа -произведение матрицы A на матрицу B слева Перестановочные матрицы: Пример. Вычислить произведение матрицы А на матрицу В справа:

Пример. Вычислить произведение матрицы В на матрицу А слева.

Пример. Доказать, что матрицы А и В перестановочные

Определители матриц Определитель матрицы второго порядка это число, равное разности произведений элементов главной и побочной диагоналей матрицы

Пример. Вычислить определитель матрицы

Минор элемента матрицы третьего порядка: определитель матрицы второго порядка, получающейся из данной матрицы вычеркиванием i-ой строки и k-гo столбца, на пересечении которых находится этот элемент.

Алгебраическое дополнение элемента матрицы третьего порядка: число, равное произведению минора этого элемента на Пример. .

Определитель матрицы третьего порядка: число, равное сумме произведений элементов любой строки (столбца) матрицы на их алгебраические дополнения - разложение определителя по строке

Пример. Вычислить определитель матрицы разложением по первой строке

Пример. Вычислить определитель матрицы разложением по второму столбцу

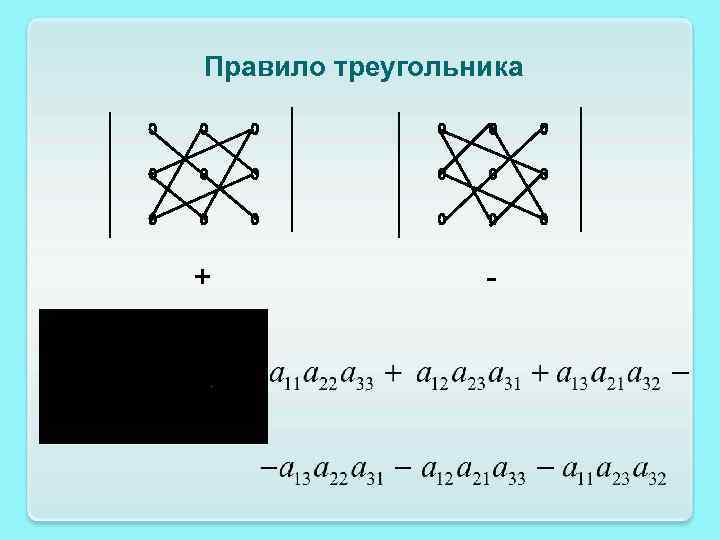Правило треугольника + -

Пример. Вычислить определитель матрицы по правилу треугольника

Пример. Вычислить определитель, разложив его по элементам первого столбца

Пример. Вычислить определитель, используя правило треугольника

Определители высших порядков

Определитель матрицы n-го порядка: число, равное сумме произведений элементов первой строки матрицы на их алгебраические дополнения

Основные свойства определителей 1. Теорема разложения. Определитель матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения. 2. Определитель транспонированной матрицы равен определителю исходной матрицы 3. Определитель с нулевой строкой (столбцом) равен нулю.

4. При перестановке двух строк (столбцов) местами определитель меняет знак. 5. Определитель с одинаковыми строками (столбцами) равен нулю. 6. Умножение определителя на число эквивалентно умножению строки (столбца) на это же число.

7. Если определитель содержит пропорциональные строки, то он равен нулю. 8. Если в некоторой строке определителя каждый элемент представить в виде суммы двух чисел, то будет выполняться равенство

9. Определитель матрицы не изменится, если к элементам какой-либо строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.

10. Сумма произведений элементов какой-либо строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) равна нулю. 11. Определитель произведения квадратных матриц равен произведению определителей этих матриц. 12.

Пример. Вычислить определитель *2+ 0

Пример. + *(-3)+

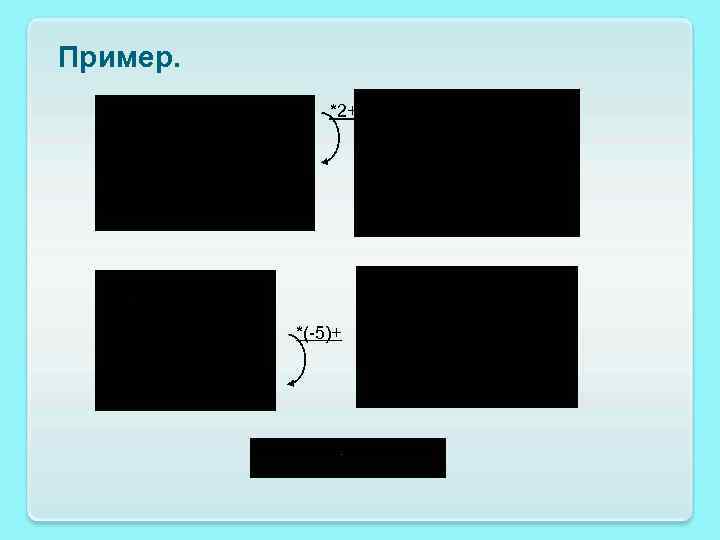Пример. *2+ *(-5)+ *(-3)+

Пример. Вычислить определитель

*(-2)+ *3+ + *(-4)+ *(-1)+

Пример. Вычислить определитель

*2+ + *3+

Обратная матрица Квадратная матрица А называется обратимой, если существует обратная к ней матрица , удовлетворяющая соотношениям Теорема. Для того, чтобы матрица А имела обратную матрицу, необходимо и достаточно, чтобы определитель ее был не равен нулю; тогда матрица А –невырожденная и

Доказательство. 1. Необходимость. Пусть квадратная матрица А имеет обратную матрицу Х. 2. Достаточность. Пусть n=3 и C- союзная матрица- составленая из алгебраических дополнений матрицы А

ч. т. д.

Свойства обратных матриц

Пример. Найти обратную матрицу для матрицы

Проверка:

Пример. Даны матрицы А, В, С. Найти матрицу

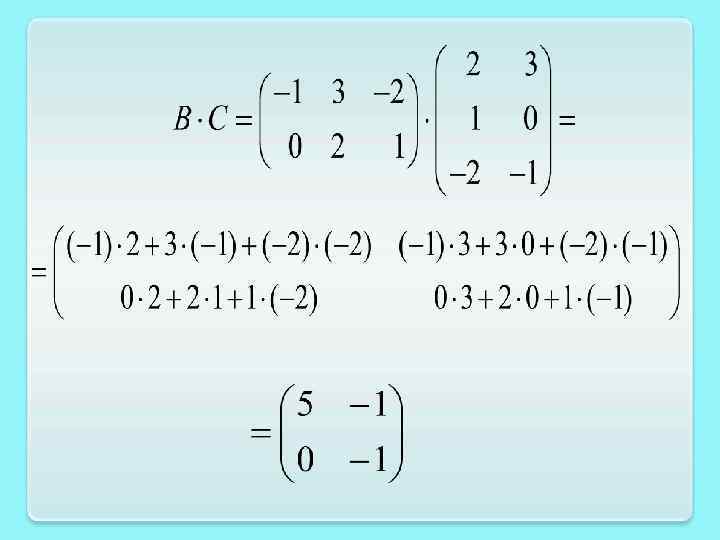
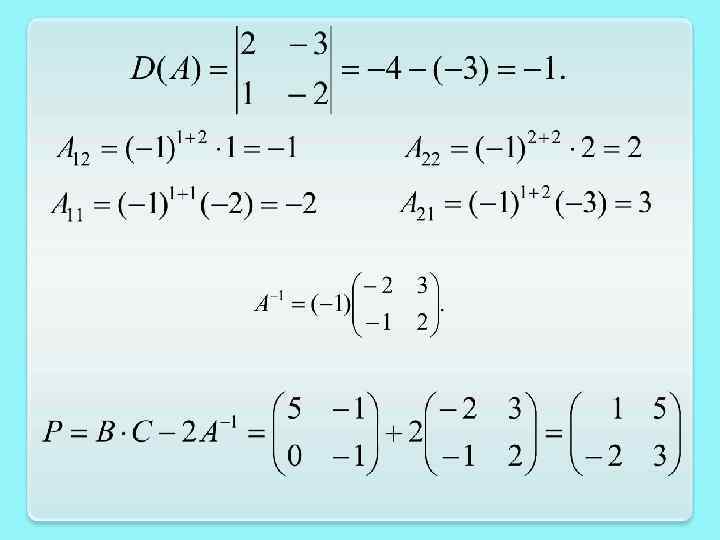
Элементарные преобразования матриц 1. Перестановка строк местами 2. Умножение строки на число 3. Прибавление к одной строке другой строки, умноженной на число 4. Отбрасывание нулевой строки 5. Транспонирование матрицы Теорема. Любая невырожденная матрица в результате конечного числа элементарных преобразований может быть преобразована в единичную матрицу

Построение обратной матрицы Пример. Найти матрицу, обратную матрице

= + *(-2)+ ~ ~ *2/3+

~ *(-6)+ ~ *3/2+ ~ *2/3+

*(-1/3) ~ *(-3/2) ~ ~

Ранг матрицы- наивысший порядок отличных от нуля миноров этой матрицы Свойства ранга: 1. Ранг нулевой матрицы равен нулю 2. 3. Элементарные преобразования на меняют ранг матрицы

Пример. Определить ранг матрицы

Пример. Определить ранг матрицы при помощи элементарных преобразований (сведением к треугольному виду) *(-2)+ ~ *(-1)+ ~ *(-2)+ ~

~ ~ ~

Спасибо за внимание! До свидания!