матем 4 лекция.ppt
- Количество слайдов: 110
 ВЫСШАЯ МАТЕМАТИКА Аналитическая геометрия в пространстве Лектор: доцент кафедры физики и высшей математики – Журавков Владислав Владимирович
ВЫСШАЯ МАТЕМАТИКА Аналитическая геометрия в пространстве Лектор: доцент кафедры физики и высшей математики – Журавков Владислав Владимирович

 Уравнением линии на плоскости XOY называется уравнение, которому удовлетворяют координаты x и y каждой точки этой линии и не удовлетворяют координаты любой точки, не лежащей на этой линии. В общем случае уравнение линии может быть записано в виде или
Уравнением линии на плоскости XOY называется уравнение, которому удовлетворяют координаты x и y каждой точки этой линии и не удовлетворяют координаты любой точки, не лежащей на этой линии. В общем случае уравнение линии может быть записано в виде или
 Пусть задана прямая, пересекающая ось у в точке В (0, в) и образующая с осью х угол α Выберем на прямой произвольную точку М(х, у).
Пусть задана прямая, пересекающая ось у в точке В (0, в) и образующая с осью х угол α Выберем на прямой произвольную точку М(х, у).
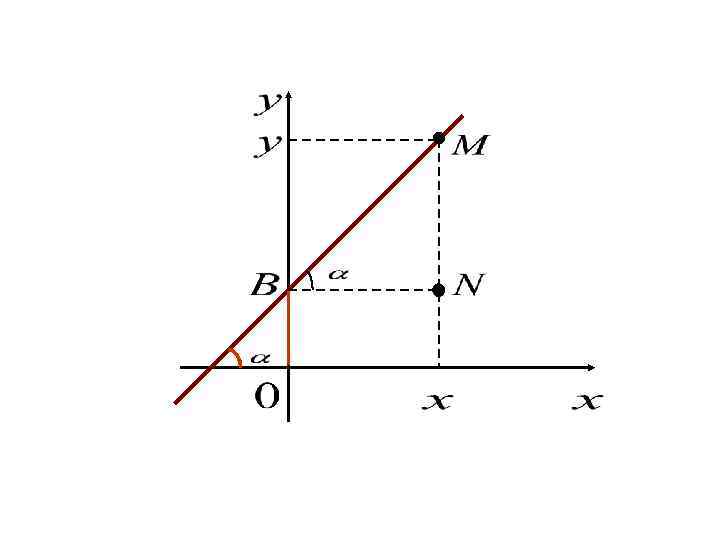
 Координаты точки N (x, в). Из треугольника BMN: k – угловой коэффициент прямой. 1
Координаты точки N (x, в). Из треугольника BMN: k – угловой коэффициент прямой. 1
 Рассмотрим частные случаи: 1 - уравнение прямой, проходящей через начало координат. 2 - уравнение прямой, параллельной оси х.
Рассмотрим частные случаи: 1 - уравнение прямой, проходящей через начало координат. 2 - уравнение прямой, параллельной оси х.
 3 - не существует т. е. у вертикальной прямой нет углового коэффициента. Уравнение прямой, параллельной оси у, в этом случае имеет вид где а – отрезок, отсекаемый прямой на оси х.
3 - не существует т. е. у вертикальной прямой нет углового коэффициента. Уравнение прямой, параллельной оси у, в этом случае имеет вид где а – отрезок, отсекаемый прямой на оси х.
 Пусть задана прямая, проходящая через заданную точку и образующая с осью х угол α
Пусть задана прямая, проходящая через заданную точку и образующая с осью х угол α
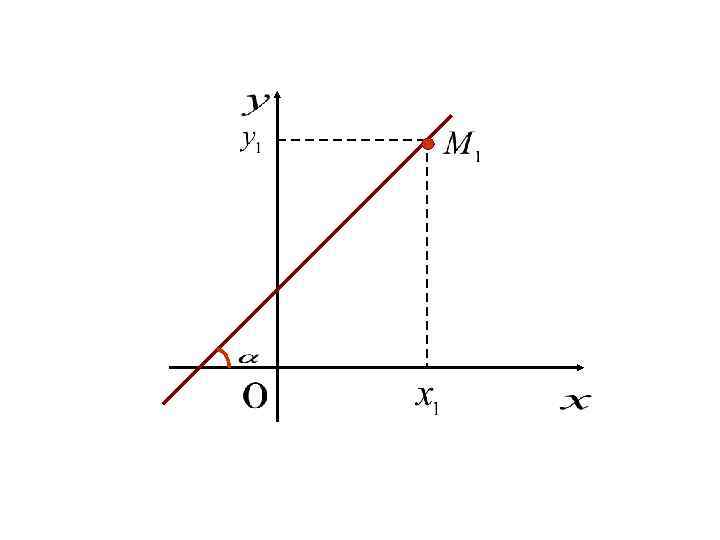
 Т. к. точка М 1 лежит на прямой, ее координаты должны удовлетворять уравнению (1): Вычитаем это уравнение из уравнения (1): 2
Т. к. точка М 1 лежит на прямой, ее координаты должны удовлетворять уравнению (1): Вычитаем это уравнение из уравнения (1): 2
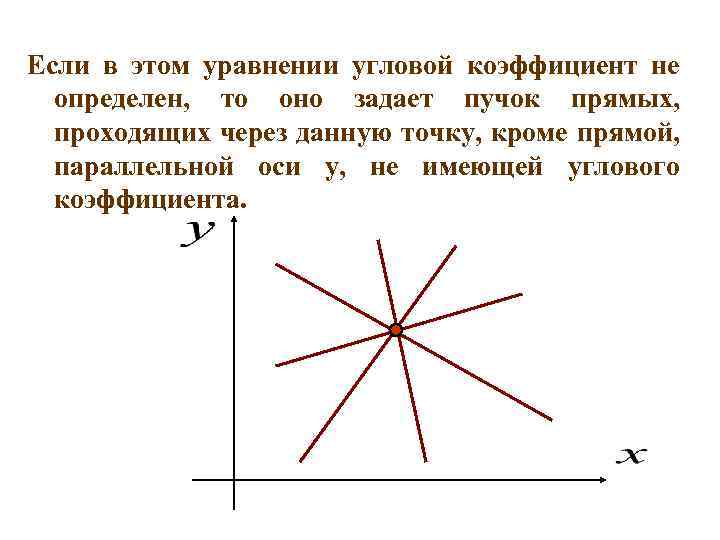 Если в этом уравнении угловой коэффициент не определен, то оно задает пучок прямых, проходящих через данную точку, кроме прямой, параллельной оси у, не имеющей углового коэффициента.
Если в этом уравнении угловой коэффициент не определен, то оно задает пучок прямых, проходящих через данную точку, кроме прямой, параллельной оси у, не имеющей углового коэффициента.
 Пусть задана прямая, проходящая через две точки: Запишем уравнение пучка прямых, проходящих через точку М 1:
Пусть задана прямая, проходящая через две точки: Запишем уравнение пучка прямых, проходящих через точку М 1:
 Т. к. точка М 2 лежит на данной прямой, подставим ее координаты в уравнение пучка прямых: Подставляем k в уравнение пучка прямых. Тем самым мы выделяем из этого пучка прямую, проходящую через две данные точки:
Т. к. точка М 2 лежит на данной прямой, подставим ее координаты в уравнение пучка прямых: Подставляем k в уравнение пучка прямых. Тем самым мы выделяем из этого пучка прямую, проходящую через две данные точки:
 или 3
или 3
 ПРИМЕР. Составить уравнение прямой, проходящей через точки А(-5, 4) и В(3, -2).
ПРИМЕР. Составить уравнение прямой, проходящей через точки А(-5, 4) и В(3, -2).
 РЕШЕНИЕ. Подставляем координаты точек в уравнение прямой, проходящей через две точки.
РЕШЕНИЕ. Подставляем координаты точек в уравнение прямой, проходящей через две точки.
 Пусть задана прямая, отсекающая на осях координат отрезки, равные а и в. Это значит, что она проходит через точки Найдем уравнение этой прямой.
Пусть задана прямая, отсекающая на осях координат отрезки, равные а и в. Это значит, что она проходит через точки Найдем уравнение этой прямой.
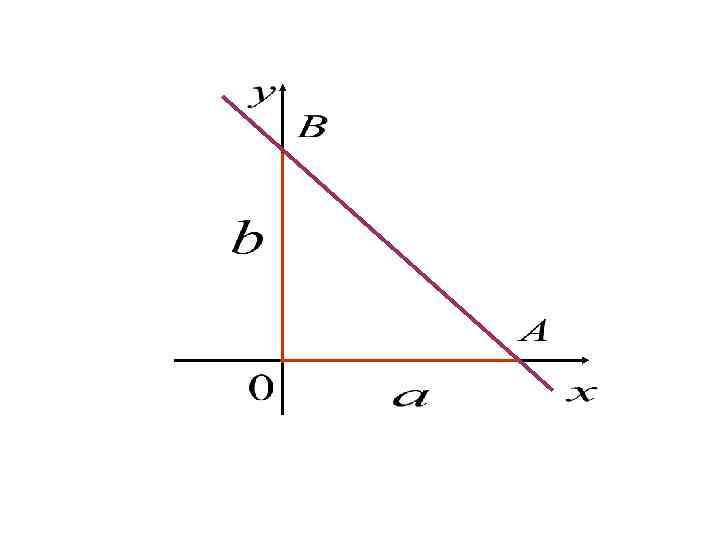
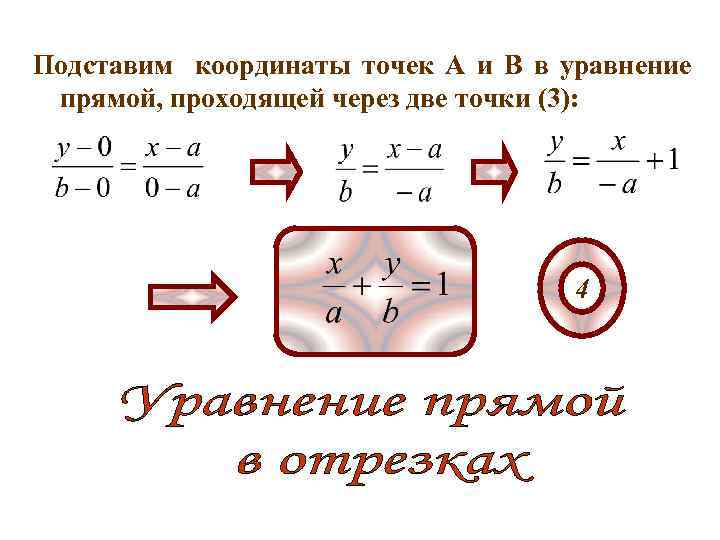 Подставим координаты точек А и В в уравнение прямой, проходящей через две точки (3): 4
Подставим координаты точек А и В в уравнение прямой, проходящей через две точки (3): 4
 ПРИМЕР. Составить уравнение прямой, проходящей через точку А(2, -1) если она отсекает от положительной полуоси у отрезок, вдвое больший, чем на положительной полуоси х.
ПРИМЕР. Составить уравнение прямой, проходящей через точку А(2, -1) если она отсекает от положительной полуоси у отрезок, вдвое больший, чем на положительной полуоси х.
 РЕШЕНИЕ. По условию задачи, Подставляем в уравнение (4): Точка А(2, -1) лежит на этой прямой, следовательно ее координаты удовлетворяют этому уравнению:
РЕШЕНИЕ. По условию задачи, Подставляем в уравнение (4): Точка А(2, -1) лежит на этой прямой, следовательно ее координаты удовлетворяют этому уравнению:
 Рассмотрим уравнение: 5 Рассмотрим частные случаи этого уравнения и покажем, что при любых значениях коэффициентов А, В (не равных нулю одновременно) и С, это уравнение есть уравнение прямой на плоскости.
Рассмотрим уравнение: 5 Рассмотрим частные случаи этого уравнения и покажем, что при любых значениях коэффициентов А, В (не равных нулю одновременно) и С, это уравнение есть уравнение прямой на плоскости.
 1 Тогда уравнение (5) можно представить в виде: Обозначим: Тогда получаем уравнение (1):
1 Тогда уравнение (5) можно представить в виде: Обозначим: Тогда получаем уравнение (1):
 2 Тогда уравнение имеет вид: - уравнение прямой, проходящей через начало координат. 3 Получаем уравнение: - уравнение прямой, параллельной оси х.
2 Тогда уравнение имеет вид: - уравнение прямой, проходящей через начало координат. 3 Получаем уравнение: - уравнение прямой, параллельной оси х.
 4 Тогда уравнение имеет вид: - уравнение оси х. 5 Получаем уравнение: - уравнение прямой, параллельной оси у.
4 Тогда уравнение имеет вид: - уравнение оси х. 5 Получаем уравнение: - уравнение прямой, параллельной оси у.
 6 Тогда уравнение имеет вид: - уравнение оси у. Таким образом, при любых значениях коэффициентов А, В (не равных нулю одновременно) и С, уравнение (5) есть уравнение прямой на плоскости. Это
6 Тогда уравнение имеет вид: - уравнение оси у. Таким образом, при любых значениях коэффициентов А, В (не равных нулю одновременно) и С, уравнение (5) есть уравнение прямой на плоскости. Это
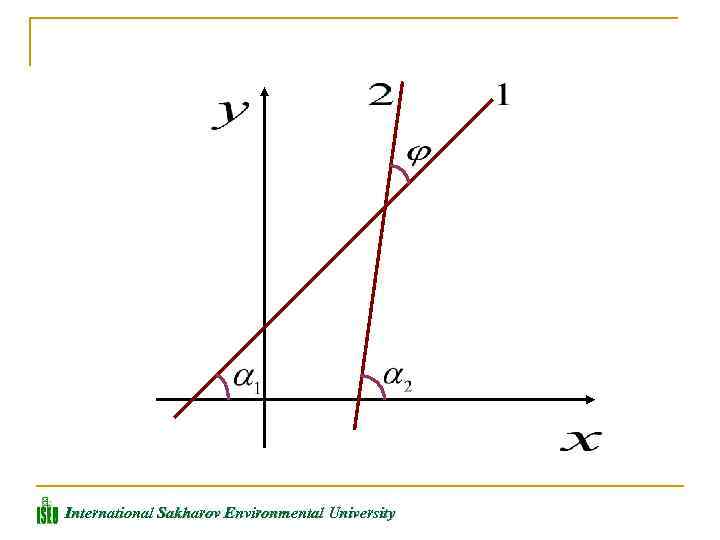
 Пусть заданы две прямые Выразим угол между этими прямыми через их угловые коэффициенты. International Sakharov Environmental University
Пусть заданы две прямые Выразим угол между этими прямыми через их угловые коэффициенты. International Sakharov Environmental University
 International Sakharov Environmental University
International Sakharov Environmental University
 International Sakharov Environmental University
International Sakharov Environmental University
 Стрелка указывает, что угол отсчитывается против часовой стрелки от прямой 1 к прямой 2. International Sakharov Environmental University
Стрелка указывает, что угол отсчитывается против часовой стрелки от прямой 1 к прямой 2. International Sakharov Environmental University
 Если прямые 1 и 2 параллельны, то International Sakharov Environmental University
Если прямые 1 и 2 параллельны, то International Sakharov Environmental University
 Две прямые параллельны тогда и только тогда, когда их угловые коэффициенты равны. International Sakharov Environmental University
Две прямые параллельны тогда и только тогда, когда их угловые коэффициенты равны. International Sakharov Environmental University
 Если прямые 1 и 2 перпендикулярны, то International Sakharov Environmental University
Если прямые 1 и 2 перпендикулярны, то International Sakharov Environmental University
 Две прямые перпендикулярны тогда и только тогда, когда их угловые коэффициенты обратны по величине и противоположны по знаку. International Sakharov Environmental University
Две прямые перпендикулярны тогда и только тогда, когда их угловые коэффициенты обратны по величине и противоположны по знаку. International Sakharov Environmental University
 Если прямые заданы общими уравнениями International Sakharov Environmental University
Если прямые заданы общими уравнениями International Sakharov Environmental University
 Пусть даны две прямые Если они не параллельны, то можно найти точку их пересечения. Т. к. эта точка принадлежит обеим прямым, то ее координаты должны удовлетворять системе уравнений: Решение этой системы дает единственную точку пересечения. International Sakharov Environmental University
Пусть даны две прямые Если они не параллельны, то можно найти точку их пересечения. Т. к. эта точка принадлежит обеим прямым, то ее координаты должны удовлетворять системе уравнений: Решение этой системы дает единственную точку пересечения. International Sakharov Environmental University
 ПРИМЕР. Составить уравнения прямых, проходящих через точку А(2, 1), одна из которых параллельна, а другая перпендикулярна прямой International Sakharov Environmental University
ПРИМЕР. Составить уравнения прямых, проходящих через точку А(2, 1), одна из которых параллельна, а другая перпендикулярна прямой International Sakharov Environmental University
 РЕШЕНИЕ: 1. По условию параллельности прямых Найдем угловой прямой: коэффициент заданной Тогда Т. к. точка А лежит на искомой прямой, то ее координаты удовлетворяют этому уравнению: International Sakharov Environmental University
РЕШЕНИЕ: 1. По условию параллельности прямых Найдем угловой прямой: коэффициент заданной Тогда Т. к. точка А лежит на искомой прямой, то ее координаты удовлетворяют этому уравнению: International Sakharov Environmental University
 И уравнение искомой прямой будет: 2. По условию перпендикулярности прямых Найдем угловой коэффициент искомой прямой: International Sakharov Environmental University
И уравнение искомой прямой будет: 2. По условию перпендикулярности прямых Найдем угловой коэффициент искомой прямой: International Sakharov Environmental University
 Снова координаты точки А удовлетворяют этому уравнению: И уравнение искомой прямой будет: International Sakharov Environmental University
Снова координаты точки А удовлетворяют этому уравнению: И уравнение искомой прямой будет: International Sakharov Environmental University
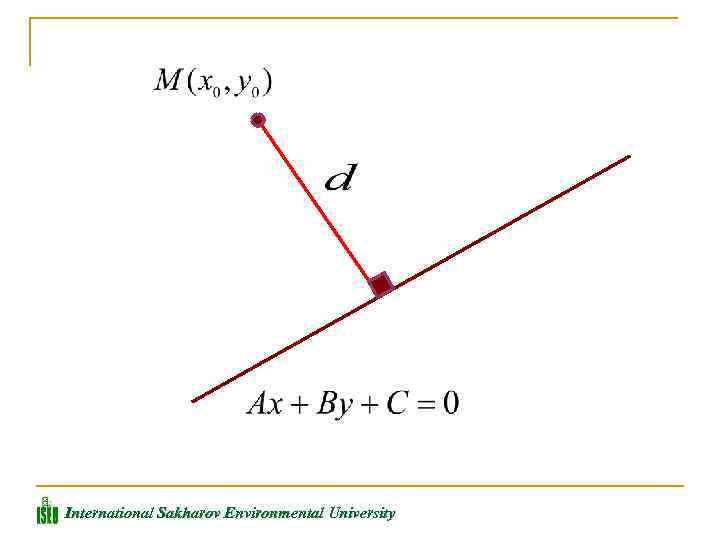
 Пусть дана точка М(х0, у0) и прямая Под расстоянием от точки М до прямой понимается длина перпендикуляра d, опущенного из точки М на данную прямую. International Sakharov Environmental University
Пусть дана точка М(х0, у0) и прямая Под расстоянием от точки М до прямой понимается длина перпендикуляра d, опущенного из точки М на данную прямую. International Sakharov Environmental University
 International Sakharov Environmental University
International Sakharov Environmental University
 ПРИМЕР. Найти расстояние между параллельными прямыми International Sakharov Environmental University
ПРИМЕР. Найти расстояние между параллельными прямыми International Sakharov Environmental University
 РЕШЕНИЕ: Возьмем на одной из прямых, например, на первой, произвольную точку А(0, 6). Тогда искомое расстояние это перпендикуляр от точки А до второй прямой : International Sakharov Environmental University
РЕШЕНИЕ: Возьмем на одной из прямых, например, на первой, произвольную точку А(0, 6). Тогда искомое расстояние это перпендикуляр от точки А до второй прямой : International Sakharov Environmental University
 Окружность и эллипс относятся к кривым второго порядка, которые описываются уравнениями второй степени с двумя переменными. Пусть дана окружность радиуса R с центром в точке О(х0, у0). Найдем ее уравнение. Выберем на окружности произвольную точку М(х, у). International Sakharov Environmental University
Окружность и эллипс относятся к кривым второго порядка, которые описываются уравнениями второй степени с двумя переменными. Пусть дана окружность радиуса R с центром в точке О(х0, у0). Найдем ее уравнение. Выберем на окружности произвольную точку М(х, у). International Sakharov Environmental University
 International Sakharov Environmental University
International Sakharov Environmental University
 Для точки М выполняется равенство: Используем формулу расстояния между двумя точками: Возводим обе части выражения в квадрат: International Sakharov Environmental University
Для точки М выполняется равенство: Используем формулу расстояния между двумя точками: Возводим обе части выражения в квадрат: International Sakharov Environmental University
 Если центр окружности лежит в начале координат (0, 0): International Sakharov Environmental University
Если центр окружности лежит в начале координат (0, 0): International Sakharov Environmental University
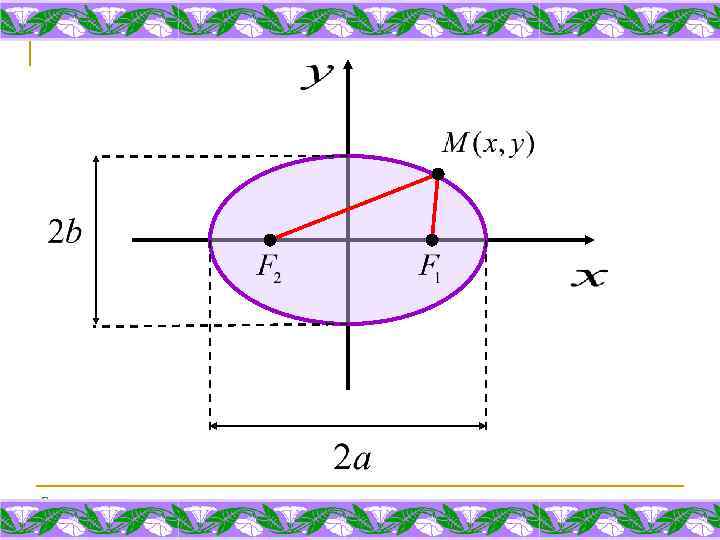
 ЭЛЛИПСОМ называется множество точек плоскости, сумма расстояний от каждой до двух данных точек, называемых фокусами, есть величина постоянная. International Sakharov Environmental University
ЭЛЛИПСОМ называется множество точек плоскости, сумма расстояний от каждой до двух данных точек, называемых фокусами, есть величина постоянная. International Sakharov Environmental University
 International Sakharov Environmental University
International Sakharov Environmental University
 Введем обозначения: a – большая полуось эллипса b – малая полуось эллипса Для любой точки М(х, у), принадлежащей эллипсу, по определению выполняется равенство: International Sakharov Environmental University
Введем обозначения: a – большая полуось эллипса b – малая полуось эллипса Для любой точки М(х, у), принадлежащей эллипсу, по определению выполняется равенство: International Sakharov Environmental University
 Для того, чтобы точка М(х, у) принадлежала эллипсу, необходимо и достаточно, чтобы ее координаты удовлетворяли уравнению 1 где International Sakharov Environmental University
Для того, чтобы точка М(х, у) принадлежала эллипсу, необходимо и достаточно, чтобы ее координаты удовлетворяли уравнению 1 где International Sakharov Environmental University
 International Sakharov Environmental University
International Sakharov Environmental University
 Отношение фокусного расстояния к длине большой оси эллипса называется ЭКСЦЕНТРИСИТЕТОМ International Sakharov Environmental University
Отношение фокусного расстояния к длине большой оси эллипса называется ЭКСЦЕНТРИСИТЕТОМ International Sakharov Environmental University
 Для эллипса Следовательно, для эллипса Чем меньше отношение малой и большой полуосей, тем больше эксцентриситет и тем более вытянутым будет эллипс вдоль оси х, и наоборот. При имеем окружность. International Sakharov Environmental University
Для эллипса Следовательно, для эллипса Чем меньше отношение малой и большой полуосей, тем больше эксцентриситет и тем более вытянутым будет эллипс вдоль оси х, и наоборот. При имеем окружность. International Sakharov Environmental University
 Пусть дан эллипс: Это уравнение эквивалентно параметрических уравнений: Проверим: International Sakharov Environmental University системе двух
Пусть дан эллипс: Это уравнение эквивалентно параметрических уравнений: Проверим: International Sakharov Environmental University системе двух
 International Sakharov Environmental University
International Sakharov Environmental University
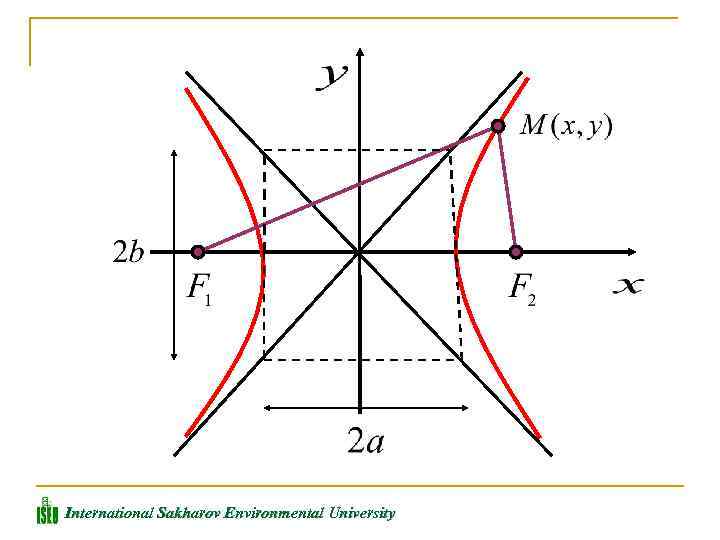
 ГИПЕРБОЛОЙ называется множество точек плоскости, абсолютная величина разности расстояний от каждой из которых до двух заданных точек, называемых фокусами, есть величина постоянная (меньшая, чем расстояние между фокусами) International Sakharov Environmental University
ГИПЕРБОЛОЙ называется множество точек плоскости, абсолютная величина разности расстояний от каждой из которых до двух заданных точек, называемых фокусами, есть величина постоянная (меньшая, чем расстояние между фокусами) International Sakharov Environmental University
 International Sakharov Environmental University
International Sakharov Environmental University
 Введем обозначения: a – действительная полуось гиперболы b – мнимая полуось гиперболы Для любой точки М(х, у), принадлежащей гиперболе, по определению выполняется равенство: International Sakharov Environmental University
Введем обозначения: a – действительная полуось гиперболы b – мнимая полуось гиперболы Для любой точки М(х, у), принадлежащей гиперболе, по определению выполняется равенство: International Sakharov Environmental University
 Прямые, проходящие через начало координат и имеющие угловые коэффициенты и называются асимптотами гиперболы. Асимптоты делят плоскость на 4 области, в двух из которых расположена гипербола. Точки гиперболы по мере удавления от оси у приближаются к асимптотам, т. е. расстояние между точками гиперболы и асимптотой при увеличении х уменьшается и стремится к нулю. International Sakharov Environmental University
Прямые, проходящие через начало координат и имеющие угловые коэффициенты и называются асимптотами гиперболы. Асимптоты делят плоскость на 4 области, в двух из которых расположена гипербола. Точки гиперболы по мере удавления от оси у приближаются к асимптотам, т. е. расстояние между точками гиперболы и асимптотой при увеличении х уменьшается и стремится к нулю. International Sakharov Environmental University
 Для того, чтобы точка М(х, у) принадлежала гиперболе, необходимо и достаточно, чтобы ее координаты удовлетворяли уравнению 2 где International Sakharov Environmental University
Для того, чтобы точка М(х, у) принадлежала гиперболе, необходимо и достаточно, чтобы ее координаты удовлетворяли уравнению 2 где International Sakharov Environmental University
 International Sakharov Environmental University
International Sakharov Environmental University
 Отношение фокусного расстояния к длине действительной оси гиперболы называется ЭКСЦЕНТРИСИТЕТОМ International Sakharov Environmental University
Отношение фокусного расстояния к длине действительной оси гиперболы называется ЭКСЦЕНТРИСИТЕТОМ International Sakharov Environmental University
 Для гиперболы Следовательно, для гиперболы Чем меньше отношение мнимой и действительной полуосей, тем меньше эксцентриситет и тем более гипербола будет прижата к оси х, и наоборот. International Sakharov Environmental University
Для гиперболы Следовательно, для гиперболы Чем меньше отношение мнимой и действительной полуосей, тем меньше эксцентриситет и тем более гипербола будет прижата к оси х, и наоборот. International Sakharov Environmental University
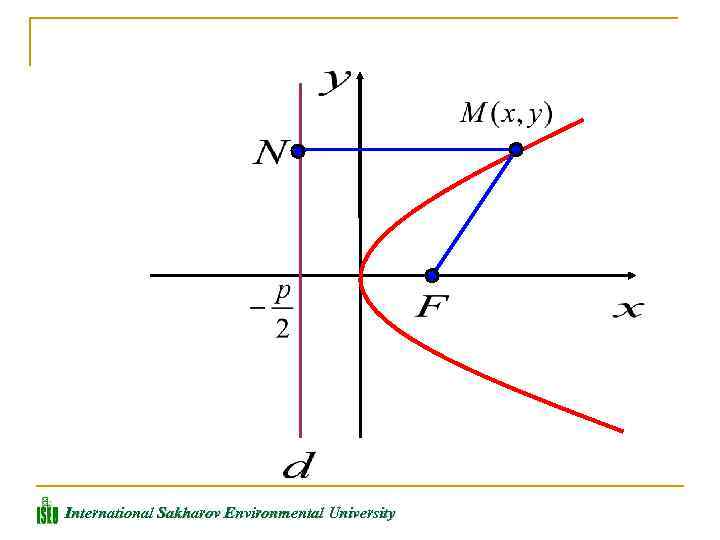
 ПАРАБОЛОЙ называется множество точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом параболы и данной прямой, называемой директрисой. International Sakharov Environmental University
ПАРАБОЛОЙ называется множество точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом параболы и данной прямой, называемой директрисой. International Sakharov Environmental University
 International Sakharov Environmental University
International Sakharov Environmental University
 Введем обозначения: Расстояние между фокусом и директрисой параболы равно р. Для любой точки М(х, у), принадлежащей параболе, по определению выполняется равенство: International Sakharov Environmental University
Введем обозначения: Расстояние между фокусом и директрисой параболы равно р. Для любой точки М(х, у), принадлежащей параболе, по определению выполняется равенство: International Sakharov Environmental University
 Для того, чтобы точка М(х, у) принадлежала параболе, необходимо и достаточно, чтобы ее координаты удовлетворяли уравнению 3 International Sakharov Environmental University
Для того, чтобы точка М(х, у) принадлежала параболе, необходимо и достаточно, чтобы ее координаты удовлетворяли уравнению 3 International Sakharov Environmental University
 International Sakharov Environmental University
International Sakharov Environmental University
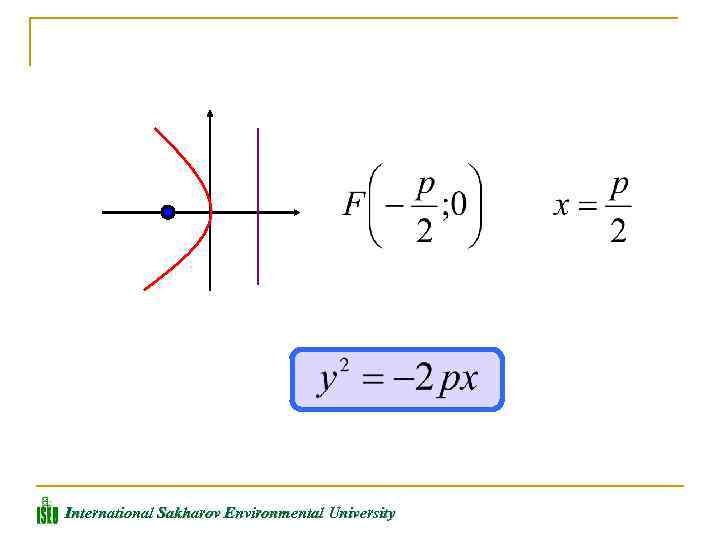
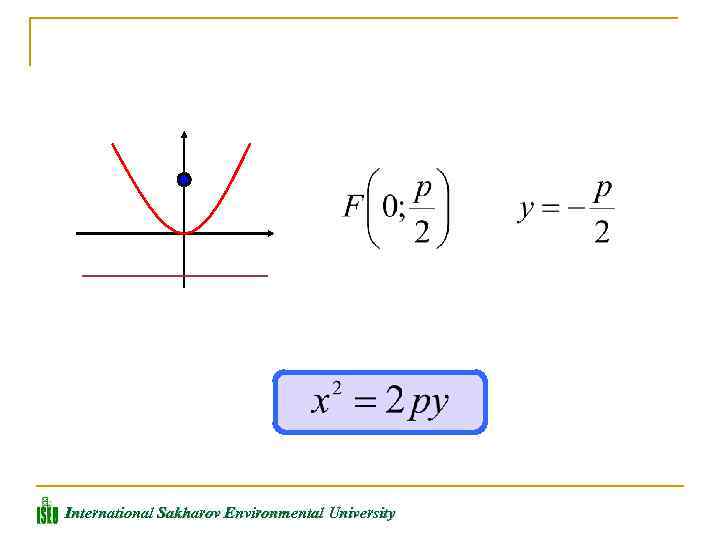
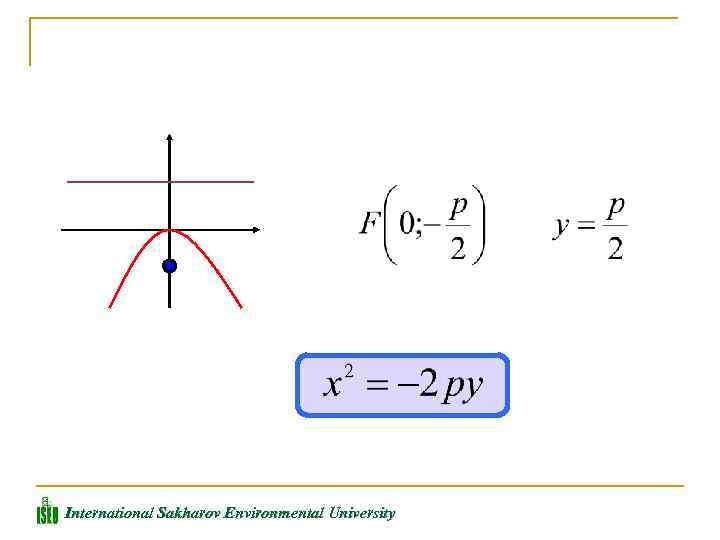
 Уравнение директрисы параболы имеет вид: Расстояние называется фокальным радиусом точки М, р называется параметром параболы. В зависимости от значения этих параметров, возможны различные способы ориентации параболы на плоскости. International Sakharov Environmental University
Уравнение директрисы параболы имеет вид: Расстояние называется фокальным радиусом точки М, р называется параметром параболы. В зависимости от значения этих параметров, возможны различные способы ориентации параболы на плоскости. International Sakharov Environmental University
 International Sakharov Environmental University
International Sakharov Environmental University
 International Sakharov Environmental University
International Sakharov Environmental University
 International Sakharov Environmental University
International Sakharov Environmental University
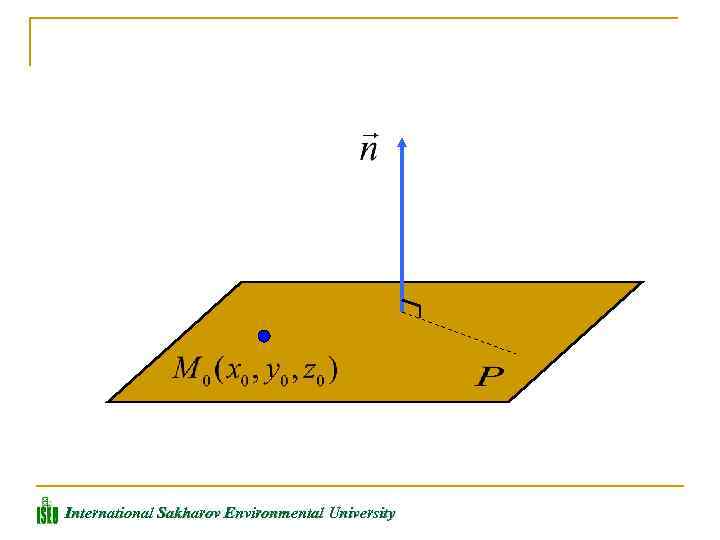
 Пусть плоскость Р, проходит через заданную точку и перпендикулярна вектору Этот вектор называется нормальным вектором плоскости Р. International Sakharov Environmental University
Пусть плоскость Р, проходит через заданную точку и перпендикулярна вектору Этот вектор называется нормальным вектором плоскости Р. International Sakharov Environmental University
 International Sakharov Environmental University
International Sakharov Environmental University
 Выберем на плоскости произвольную точку Тогда и Тогда скалярное произведение этих векторов должно быть равно нулю: Распишем его в координатах: International Sakharov Environmental University
Выберем на плоскости произвольную точку Тогда и Тогда скалярное произведение этих векторов должно быть равно нулю: Распишем его в координатах: International Sakharov Environmental University
 1 International Sakharov Environmental University
1 International Sakharov Environmental University
 Раскроем скобки в уравнении (1): Обозначим: International Sakharov Environmental University
Раскроем скобки в уравнении (1): Обозначим: International Sakharov Environmental University
 2 International Sakharov Environmental University
2 International Sakharov Environmental University
 Пусть плоскость Р отсекает на осях координат отрезки, равные соответственно a, b, c. International Sakharov Environmental University
Пусть плоскость Р отсекает на осях координат отрезки, равные соответственно a, b, c. International Sakharov Environmental University
 3 International Sakharov Environmental University
3 International Sakharov Environmental University
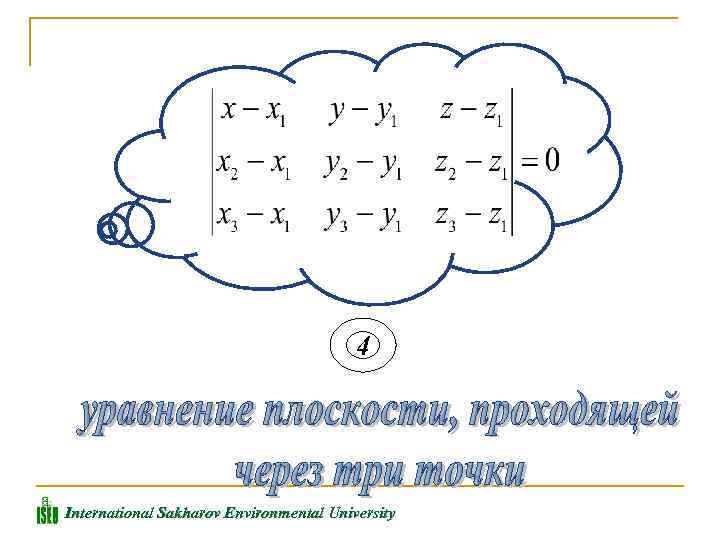
 Пусть задана плоскость, проходящая через три точки: Тогда уравнение записать в определителя: этой виде International Sakharov Environmental University плоскости можно равенства нулю
Пусть задана плоскость, проходящая через три точки: Тогда уравнение записать в определителя: этой виде International Sakharov Environmental University плоскости можно равенства нулю
 4 International Sakharov Environmental University
4 International Sakharov Environmental University
 Пусть даны две плоскости с нормальными векторами Условия параллельности и перпендикулярности плоскостей определяются условиями коллинеарности и перпендикулярности их нормальных векторов: International Sakharov Environmental University
Пусть даны две плоскости с нормальными векторами Условия параллельности и перпендикулярности плоскостей определяются условиями коллинеарности и перпендикулярности их нормальных векторов: International Sakharov Environmental University
 International Sakharov Environmental University
International Sakharov Environmental University
 International Sakharov Environmental University
International Sakharov Environmental University
 Пусть дана точка И плоскость Тогда расстояние от точки до плоскости определяется по формуле: International Sakharov Environmental University
Пусть дана точка И плоскость Тогда расстояние от точки до плоскости определяется по формуле: International Sakharov Environmental University
 International Sakharov Environmental University
International Sakharov Environmental University
 Прямая в пространстве может быть задана как линия пересечения двух плоскостей. Тогда любая точка прямой будет удовлетворять системе уравнений, задающих данные плоскости: International Sakharov Environmental University
Прямая в пространстве может быть задана как линия пересечения двух плоскостей. Тогда любая точка прямой будет удовлетворять системе уравнений, задающих данные плоскости: International Sakharov Environmental University
 1 International Sakharov Environmental University
1 International Sakharov Environmental University
 Пусть прямая проходит через точку параллельно вектору Этот вектор называется направляющим вектором прямой. International Sakharov Environmental University
Пусть прямая проходит через точку параллельно вектору Этот вектор называется направляющим вектором прямой. International Sakharov Environmental University
 Выберем на прямой произвольную точку и рассмотрим вектор Уравнения прямой могут быть получены из условия коллинеарности этого вектора и направляющего вектора прямой: International Sakharov Environmental University
Выберем на прямой произвольную точку и рассмотрим вектор Уравнения прямой могут быть получены из условия коллинеарности этого вектора и направляющего вектора прямой: International Sakharov Environmental University
 2 International Sakharov Environmental University
2 International Sakharov Environmental University
 Пусть прямая проходит через две точки Выберем на прямой произвольную точку International Sakharov Environmental University
Пусть прямая проходит через две точки Выберем на прямой произвольную точку International Sakharov Environmental University
 3 International Sakharov Environmental University
3 International Sakharov Environmental University
 Пусть заданы две прямые Острый угол между этими прямыми находится из скалярного произведения векторов International Sakharov Environmental University
Пусть заданы две прямые Острый угол между этими прямыми находится из скалярного произведения векторов International Sakharov Environmental University
 International Sakharov Environmental University
International Sakharov Environmental University
 International Sakharov Environmental University
International Sakharov Environmental University
 International Sakharov Environmental University
International Sakharov Environmental University
 Пусть прямая задана уравнением: И пусть задана плоскость Рассмотрим возможные случаи ориентации прямой и плоскости: International Sakharov Environmental University
Пусть прямая задана уравнением: И пусть задана плоскость Рассмотрим возможные случаи ориентации прямой и плоскости: International Sakharov Environmental University
 1 Прямая принадлежит плоскости. Тогда направляющий вектор прямой ортогонален плоскости нормальному И пусть точка принадлежит прямой. International Sakharov Environmental University вектору
1 Прямая принадлежит плоскости. Тогда направляющий вектор прямой ортогонален плоскости нормальному И пусть точка принадлежит прямой. International Sakharov Environmental University вектору
 Тогда выполняются следующие условия: Поскольку вектора в и этом случае перпендикулярны, и их скалярное произведение этих векторов равно нулю: 1 Поскольку точка М 0 будет принадлежать плоскости, то ее координаты удовлетворяют уравнению плоскости: 2 International Sakharov Environmental University
Тогда выполняются следующие условия: Поскольку вектора в и этом случае перпендикулярны, и их скалярное произведение этих векторов равно нулю: 1 Поскольку точка М 0 будет принадлежать плоскости, то ее координаты удовлетворяют уравнению плоскости: 2 International Sakharov Environmental University
 2 Прямая параллельна плоскости. Тогда выполняется только условие (1). 3 Прямая пересекает плоскость в одной точке. Тогда выполняется условие International Sakharov Environmental University
2 Прямая параллельна плоскости. Тогда выполняется только условие (1). 3 Прямая пересекает плоскость в одной точке. Тогда выполняется условие International Sakharov Environmental University
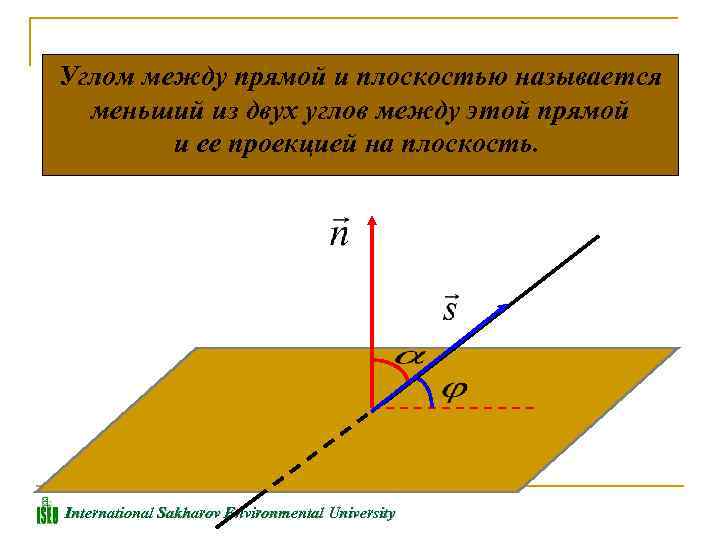 Углом между прямой и плоскостью называется меньший из двух углов между этой прямой и ее проекцией на плоскость. International Sakharov Environmental University
Углом между прямой и плоскостью называется меньший из двух углов между этой прямой и ее проекцией на плоскость. International Sakharov Environmental University
 Синус угла φ между прямой и плоскостью равен косинусу угла α между нормальным вектором плоскости и направляющим вектором прямой: Найдем угол α, как угол между двумя векторами: International Sakharov Environmental University
Синус угла φ между прямой и плоскостью равен косинусу угла α между нормальным вектором плоскости и направляющим вектором прямой: Найдем угол α, как угол между двумя векторами: International Sakharov Environmental University
 International Sakharov Environmental University
International Sakharov Environmental University
 Если прямая перпендикулярна плоскости, то направляющий вектор прямой параллелен нормальному вектору плоскости: International Sakharov Environmental University
Если прямая перпендикулярна плоскости, то направляющий вектор прямой параллелен нормальному вектору плоскости: International Sakharov Environmental University
 Если прямая параллельна плоскости, то International Sakharov Environmental University
Если прямая параллельна плоскости, то International Sakharov Environmental University


