высота образующая радиус

высота образующая радиус

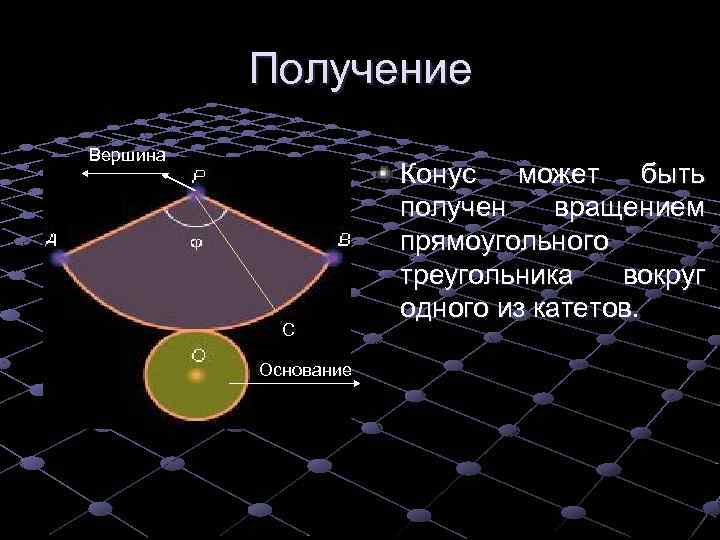
Получение Вершина Конус может быть получен вращением прямоугольного треугольника вокруг одного из катетов. С Основание

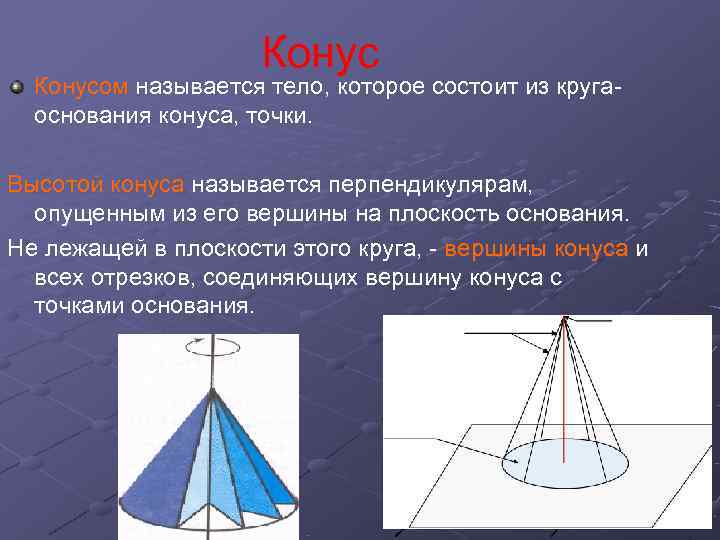
Конусом называется тело, которое состоит из круга- основания конуса, точки. Высотой конуса называется перпендикулярам, опущенным из его вершины на плоскость основания. Не лежащей в плоскости этого круга, - вершины конуса и всех отрезков, соединяющих вершину конуса с точками основания.

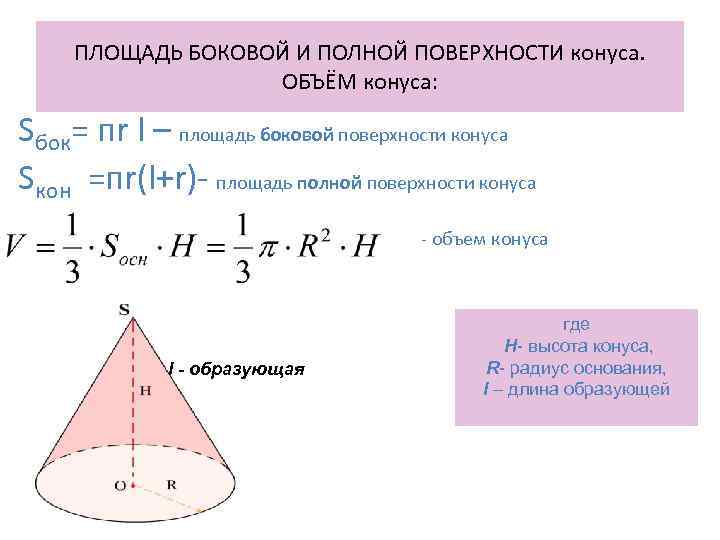
ПЛОЩАДЬ БОКОВОЙ И ПОЛНОЙ ПОВЕРХНОСТИ конуса. ОБЪЁМ конуса: Sбок= пr l – площадь боковой поверхности конуса Sкон =пr(l+r)- площадь полной поверхности конуса - объем конуса где Н- высота конуса, l - образующая R- радиус основания, l – длина образующей

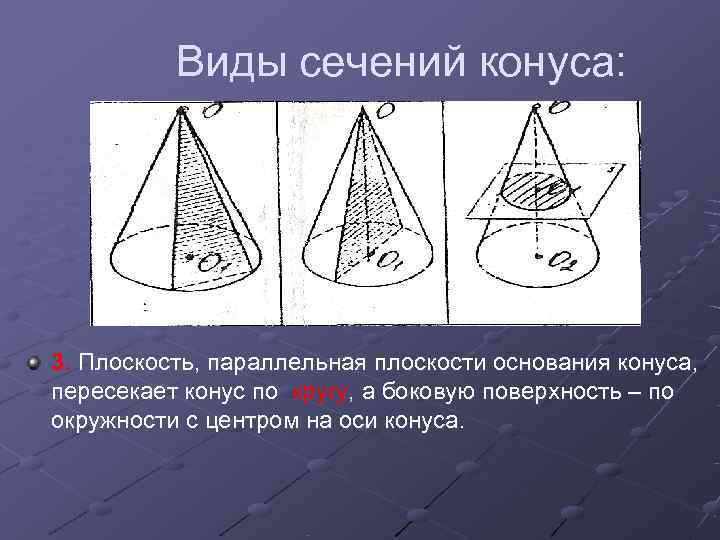
Виды сечений конуса: 3. Плоскость, параллельная плоскости основания конуса, пересекает конус по кругу, а боковую поверхность – по окружности с центром на оси конуса.

Сечения конуса Осевое( если секущая плоскость проходит через ось конуса, то сечение представляет собой равнобедренный треугольник, основание которого- диаметр основания конуса, а боковые стороны- образующие) Сечение конуса плоскостью перпендикулярной к его оси.

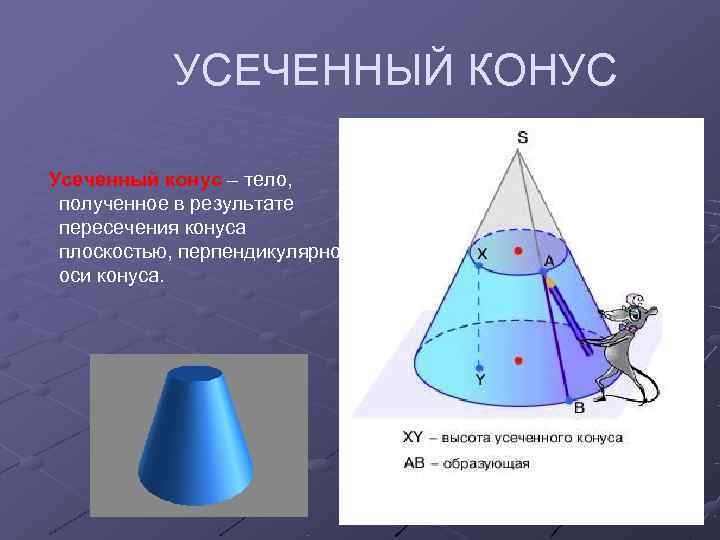
УСЕЧЕННЫЙ КОНУС Усеченный конус – тело, полученное в результате пересечения конуса плоскостью, перпендикулярной оси конуса.

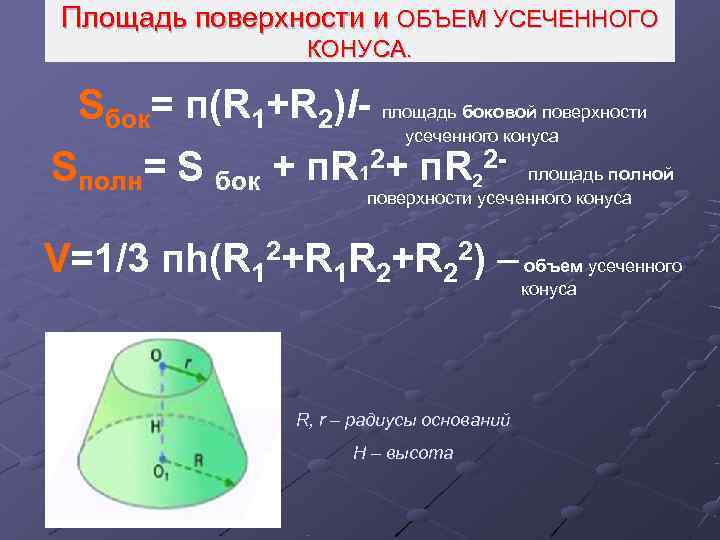
Площадь поверхности и ОБЪЕМ УСЕЧЕННОГО КОНУСА. Sбок= п(R 1+R 2)l- площадь боковой поверхности усеченного конуса Sполн= S бок + п. R 12+ п. R 22 - площадь полной поверхности усеченного конуса V=1/3 пh(R 12+R 1 R 2+R 22) – объем усеченного конуса R, r – радиусы оснований H – высота

Многогранник, описанный около конуса. Пирамидой, описанной около конуса, называется пирамида, у которой основанием служит многоугольник, описанной около основания конуса, а вершина совпадает с вершиной конуса.

Усеченный конус Возьмем произвольный конус и проведем секущую плоскость, перпендикулярную к его оси. Эта плоскость пересекается с конусом по кругу и разбивает конус на две части. Одна из частей представляет собой конус, а другая называется усеченным конусом. Площадь боковой поверхности усеченного конуса

Формулы Площадь конуса Площадь боковой поверхности Объем конуса Площадь боковой поверхности

Применение Конус можно рассмотреть в различных предметах, начиная с обычного мороженого и заканчивая техникой( носовая часть у ракеты).