Высказывания и операции над ними Высказыванием или

Высказывания и операции над ними

Высказыванием или суждением называют повествовательное предложение, что-либо утверждающее или отрицающее, о котором можно объективно судить, истинно оно или ложно. Примеры: 17 – простое число (истиное выск. ) Земля – спутник Луны (ложное выск. ) Как дела? (не явл. выск. )

Обозначения • Для обозначения высказываний используют малые латинские буквы: a, b, c, …x, … • Для обозначения истинностного значения высказывания используют знак | |: |р|-истинностное значение высказывания р. • Если р – истинное высказывание, то |р|=И или |р|=1 • Если р – ложное высказывание, то |р|=Л или |р|=0

Простые и сложные высказывания • Простым считают высказывание, которое не содержит в своей структуре более элементарных высказываний. Пример: «Москва – столица России» • Сложное высказывание состоит из простых высказываний, соединенных логической связкой. Пример: «В огороде бузина, а в Киеве дядька»

Логические операции над высказываниями: • • • Отрицание Конъюнкция Дизъюнкция Импликация Эквиваленция

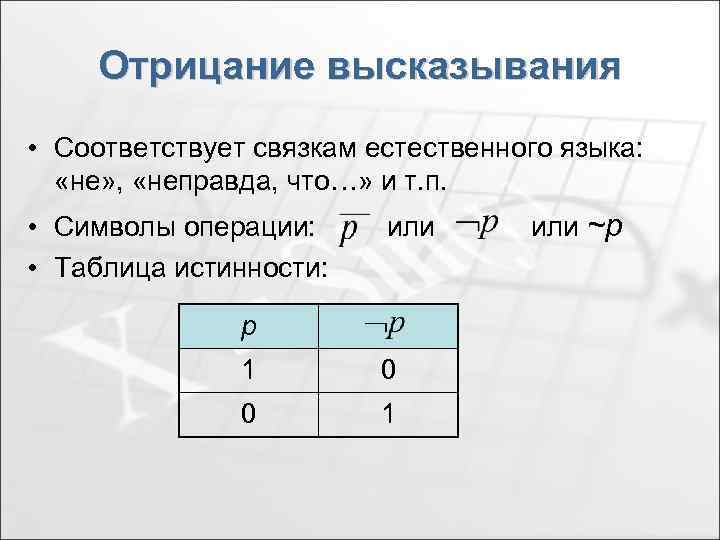Отрицание высказывания • Соответствует связкам естественного языка: «не» , «неправда, что…» и т. п. • Символы операции: • Таблица истинности: или р 1 0 0 1 или ~р

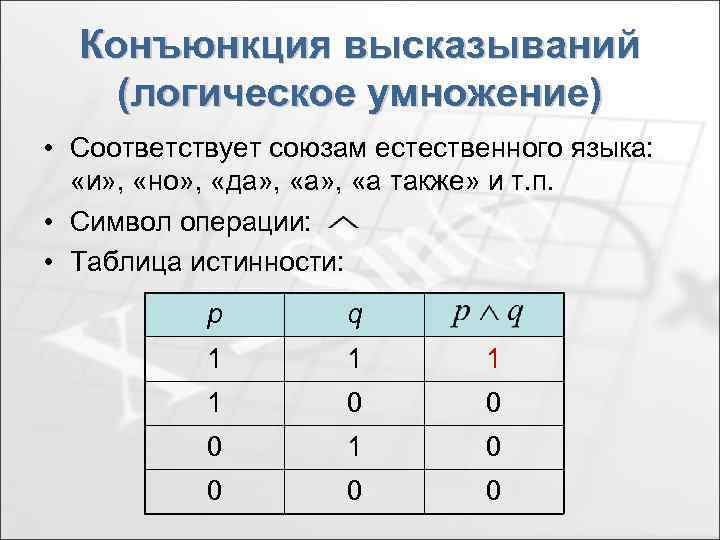Конъюнкция высказываний (логическое умножение) • Соответствует союзам естественного языка: «и» , «но» , «да» , «а также» и т. п. • Символ операции: • Таблица истинности: р q 1 1 0 0 0 1 0 0

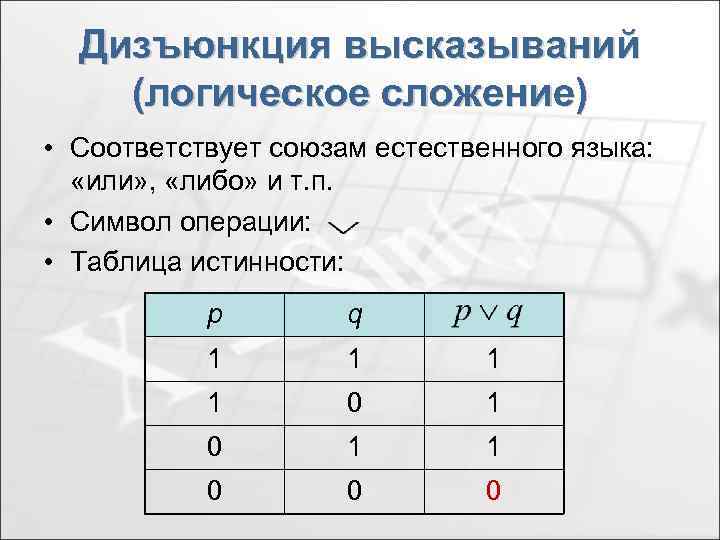Дизъюнкция высказываний (логическое сложение) • Соответствует союзам естественного языка: «или» , «либо» и т. п. • Символ операции: • Таблица истинности: р q 1 1 0 0 0

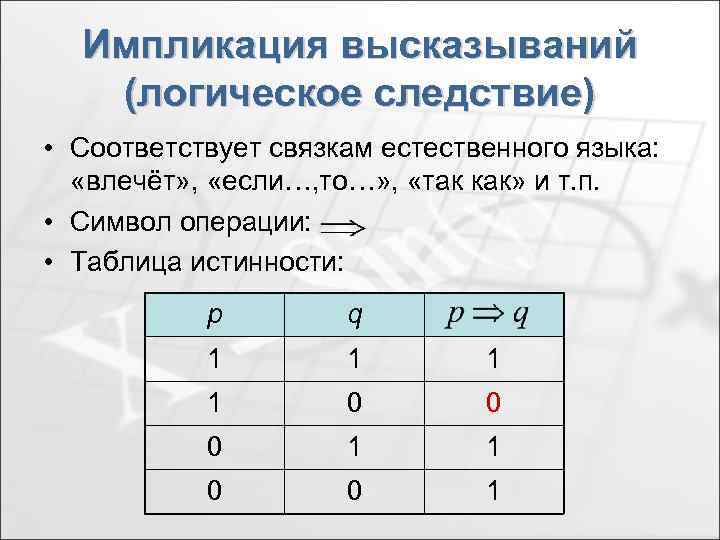Импликация высказываний (логическое следствие) • Соответствует связкам естественного языка: «влечёт» , «если…, то…» , «так как» и т. п. • Символ операции: • Таблица истинности: р q 1 1 0 0 0 1 1 0 0 1

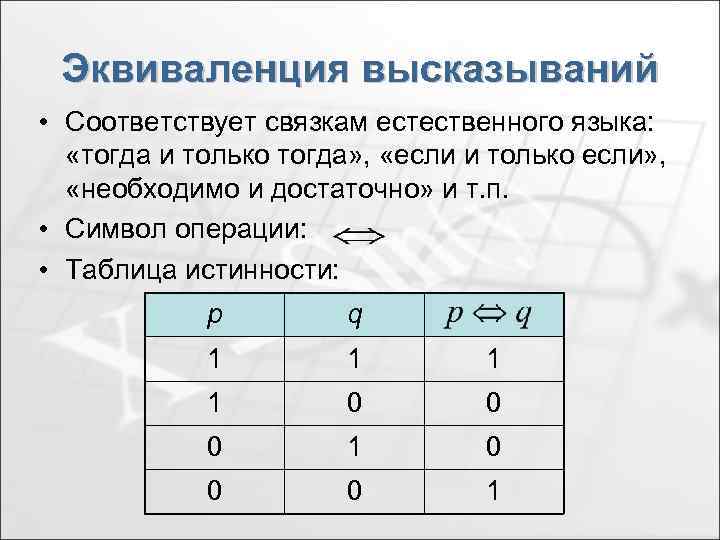Эквиваленция высказываний • Соответствует связкам естественного языка: «тогда и только тогда» , «если и только если» , «необходимо и достаточно» и т. п. • Символ операции: • Таблица истинности: р q 1 1 0 0 0 1

Формулы логики • Все простые высказывания являются формулами логики. • Если р – формула, то - формула. • Если р – формула и q - формула, то - формулы. • Каждому сложному высказыванию естественного языка соответствует определенная логическая структура, выраженная формулой логики.

Примеры • Высказыванию «Я сдам экзамен по математике, если и только если не буду пропускать занятия и научусь решать задачи» соответствует формула логики • Высказыванию «Он обязательно полюбит меня, но навряд ли это произойдет, если он узнает обо всех моих похождениях» соответствует формула

Таблица истинности формулы • Для любой формулы логики можно судить истинна она или ложна при каждом определенном наборе истинностных значений ее переменных – в каждой логически возможной ситуации. • Для определения истинностного значения формулы логики составляют таблицу истинности

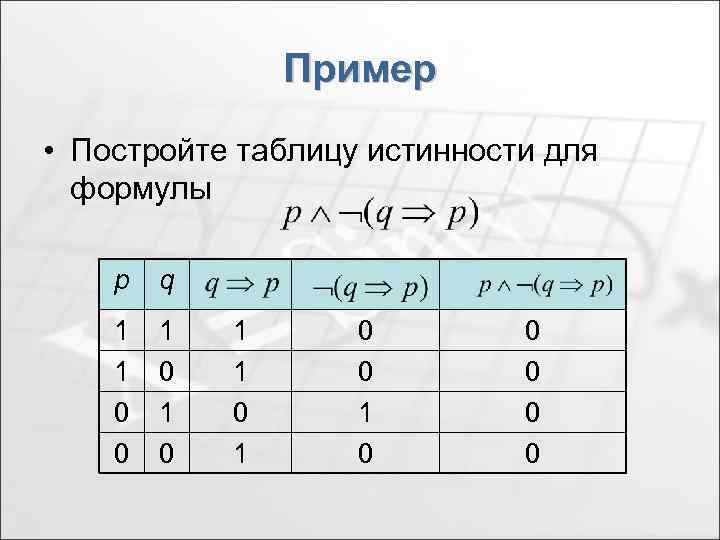Пример • Постройте таблицу истинности для формулы p q 1 1 0 0 1 0 0 0

Правила построения таблицы истинности • Число строк таблицы (число логически возможных ситуаций) равно 2 n, где n – число переменных в формуле. • Число столбцов = число переменных + число операций. • Порядок выполнения логических операций: отрицание→конъюнкция и дизъюнкция→импликация и эквиваленция. • Скобки меняют порядок действий.

Виды формул логики • Если формула принимает значение «ложь» в каждой логически возможной ситуации, ее называют тождественно ложной или противоречием • Если формула принимает значение «истина» в каждой логически возможной ситуации, ее называют тождественно истинной или общезначимой или тавтологией или логическим законом

Основные логические законы

Основные логические законы