Высказыванием называется простое повествовательное положение о котором можно

Высказыванием называется простое повествовательное положение, о котором можно сказать, что оно ложно или истинно, но не то и другое одновременно. Логическая переменная X имеет 2 значения: X={0 -"ложь" , 1 -"истина"} Логическая функция f(x 1, x 2, . . . , xn)

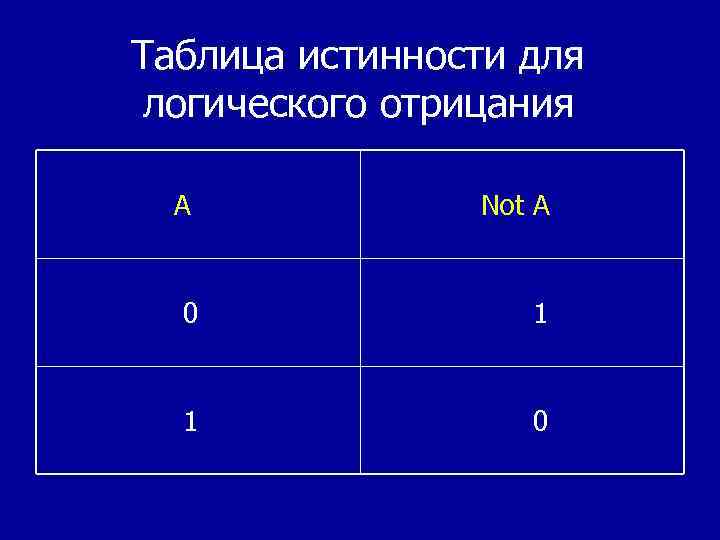Таблица истинности для логического отрицания A Not A 0 1 1 0

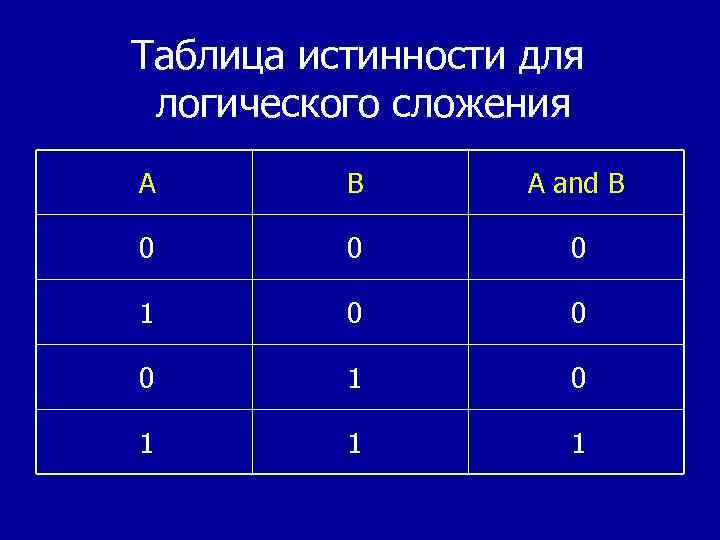Таблица истинности для логического сложения А В A and B 0 0 0 1 0 1 1 1

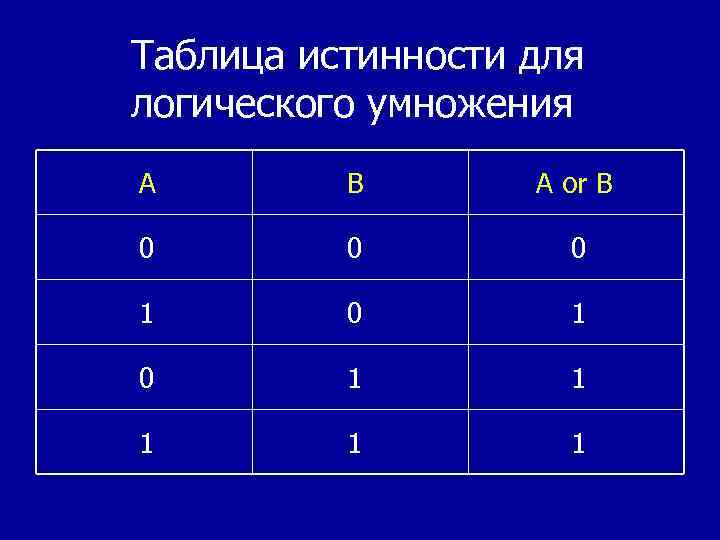Таблица истинности для логического умножения А В A or B 0 0 0 1 0 1 1 1

Вычисление выражений Дано выражение: A and B or not C and D Пусть A = "истина", B = "ложь", C ="ложь", D = "истина" Указать порядок выполнения операций и найти значение логического выражения при заданных переменных.

Законы булевой алгебры Лист 1. Законы де Моргана 1 -ый закон де Моргана: (отрицание конъюнкции) Отрицание логического умножения равносильно логическому сложению отрицаний, т. е. not (A and B) = (not A) or (not B) 2 -ой закон де Моргана: (отрицание дизъюнкции) Отрицание логического сложения равносильно логическому умножению отрицаний, т. е. not (A or B) = (not A) and (not B)

Законы булевой алгебры Лист 2 Ассоциативность сложения и умножения: X 1 or (X 2 or X 3) = (X 1 or X 2) or X 3 = X 1 or X 2 or X 3 X 1 and (X 2 and X 3) = (X 1 and X 2) and X 3 = X 1 and X 2 and X 3 Коммутативность сложения и умножения: X 1 or X 2 = X 2 or X 1 and X 2 = X 2 and X 1

Законы булевой алгебры Лист 3 Дистрибутивность умножения относительно сложения: X 1 and (X 2 or X 3) = X 1 and X 2 or X 1 and X 3 Дистрибутивность сложения относительно умножения: X 1 or (X 2 and X 3) = (X 1 or X 2) and (X 1 or X 3)

Законы булевой алгебры Лист 4 Идемпотентность (отсутствие степеней и коэффициентов): X and X = X X or X = X Закон двойного отрицания: not X = X

Соотношения исключения третьего X or X and Y = X and 1 or X and Y = X and (1 or Y) = X (поглощение) X and Y or X and not Y = X and (Y or not Y) = X and 1 = X (склеивание) X or not X and Y = (X or not X) and (X or Y) = 1 and (X or Y) = X or Y