ВЫПУКЛЫЙ АНАЛИЗ ЛЕКЦИЯ 24 8 ВЫПУКЛОЕ ПРОГРАММИРОВАНИЕ

ВЫПУКЛЫЙ АНАЛИЗ ЛЕКЦИЯ 24 8. ВЫПУКЛОЕ ПРОГРАММИРОВАНИЕ

8. ВЫПУКЛОЕ ПРОГРАММИРОВАНИЕ 8. 1. Постановка задачи выпуклого программирования. 8. 2. Седловая точка регулярной функции Лагранжа. 8. 3. Условия Слейтера.

8. ВЫПУКЛОЕ ПРОГРАММИРОВАНИЕ 8. 1. Постановка задачи выпуклого программирования. Под выпуклым программированием понимается раздел теории экстремальных задач, в котором изучаются задачи минимизации выпуклых функций на выпуклых множествах. Задача выпуклого программирования формулируется следующим образом. Задача 1. где выпуклое множество, -заданные функции, при чем функции линейные, т. е. имеют вид выпуклые, а функции

Заметим, что в сделанных предположениях множеством. является выпуклым 8. 2. Седловая точка регулярной функции Лагранжа. Для исследования задачи 1 выпуклого программирования введем понятие регулярной функции Лагранжа. Положим Определение 1. Функция определенная формулой называется регулярной функцией Лагранжа для задачи 1.

Определение 2. Пара называется седловой точкой функции Лагранжа для задачи 1, если Придадим условию (1) другую форму. Теорема 1. Для того, чтобы пара была седловой точкой для регулярной функции Лагранжа, необходимо и достаточно выполнение следующих условий: Доказательство. Необходимость. Пусть пара седловая точка функции Лагранжа. Из правого неравенства в (1) сразу следует условие 1) теоремы. Перепишем левое неравенство в (1) с учетом определения функции Лагранжа. Имеем

Отсюда выводим, что Покажем, что Очевидно, что Для всех построим вектор для всех

Выпишем конкретный вид этого вектора Подставим вектор в неравенство (2).

Таким образом, получили Отсюда выводим, что действительно теоремы. Докажем справедливость условия 2) С этой целью сконструируем вектор полагая

Тогда из неравенства (2) находим, что Отсюда Условия 2) теоремы доказаны. Необходимость доказана. , Достаточность. Пусть для некоторой пары выполнены условия 1)- 3) теоремы. Для доказательства того, что эта пара является седловой точкой функции Лагранжа достаточно установить, что она удовлетворяет левому неравенству в (1) или, что тоже самое, (3).

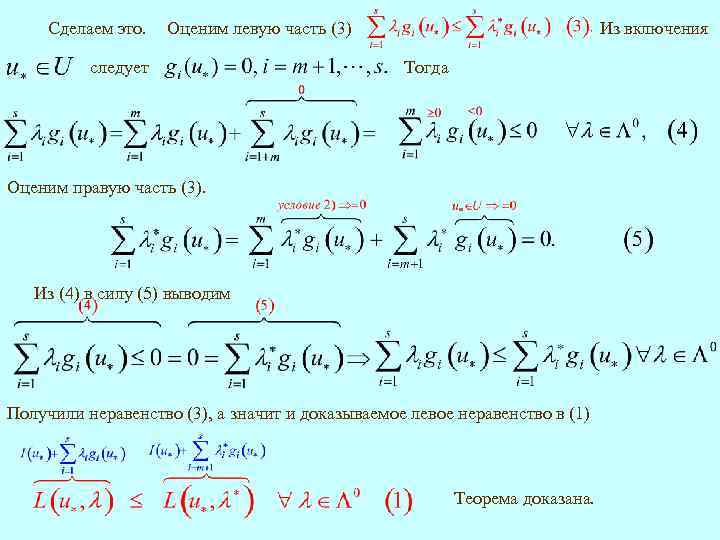Сделаем это. Из включения Оценим левую часть (3) следует Тогда Оценим правую часть (3). Из (4) в силу (5) выводим Получили неравенство (3), а значит и доказываемое левое неравенство в (1) Теорема доказана.

Выясним, как связаны между собой решение задачи 1 и седловая точка функции Лагранжа для этой задачи. С одной стороны, имеет место следующая теорема. Теорема 2. Пусть пара является седловой точкой регулярной функции Лагранжа для задачи 1. Тогда Доказательство. Из равенства (5) Из правой части неравенства (1) В частности, при из (6) выводим отсюда следует

Теорема доказана. С другой стороны, существуют примеры задач выпуклого программирования, для которых функция Лагранжа не имеет седловых точек при непустом множестве Пример 1. Пусть В этом примере множество Построим функцию Лагранжа для задачи Покажем, что функция Лагранжа не имеет седловых точек. Допустим противное. Пусть седловая точка функции Лагранжа. Тогда по теореме 2 пара Не может быть, чтобы так как при имеем

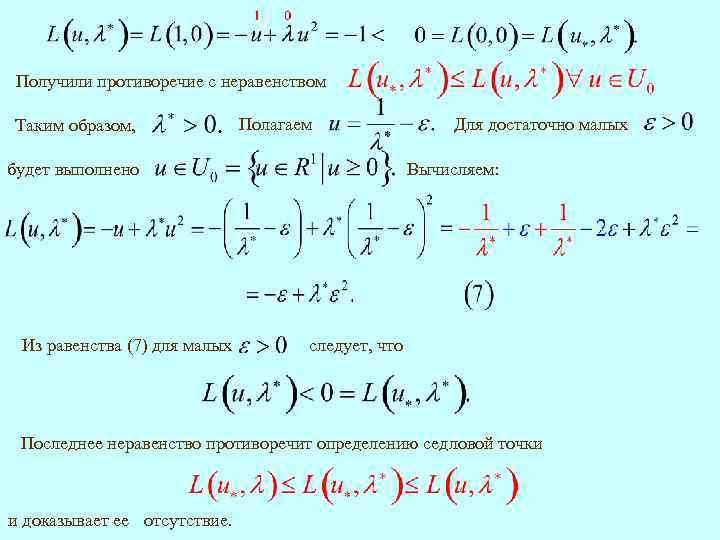Получили противоречие с неравенством Таким образом, Полагаем Вычисляем: будет выполнено Из равенства (7) для малых Для достаточно малых следует, что Последнее неравенство противоречит определению седловой точки и доказывает ее отсутствие.

8. 3. Условия Слейтера. В предыдущем пункте было установлено, что не всякая задача выпуклого программирования допускает существование седловой точки своей функции Лагранжа. Для ее существования помимо выпуклости требуется наложить некоторые дополнительные условия на ограничения. Рассмотрим частный случай ограничений задачи 1. Именно, примем, что ограничения типа равенств отсутствуют, т. е. , что Тогда определенное условием (1), называется регулярным Определение 3. Множество (выполнены условия Слейтера), если существует точка Упражнение. такая, что Доказать, что для выполнения условия Слейтера в задачах выпуклого программирования достаточно потребовать, чтобы для любого номера существовала точка для которой бы выполнялось Решение пусть таковы, что и Положим

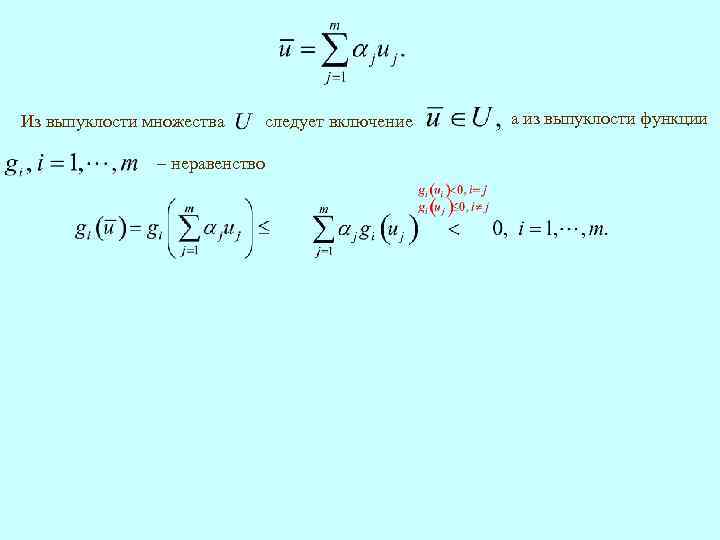Из выпуклости множества – неравенство следует включение а из выпуклости функции