ВЫПУКЛЫЙ АНАЛИЗ ЛЕКЦИЯ 1 9 6. ТЕОРЕМЫ ОБ



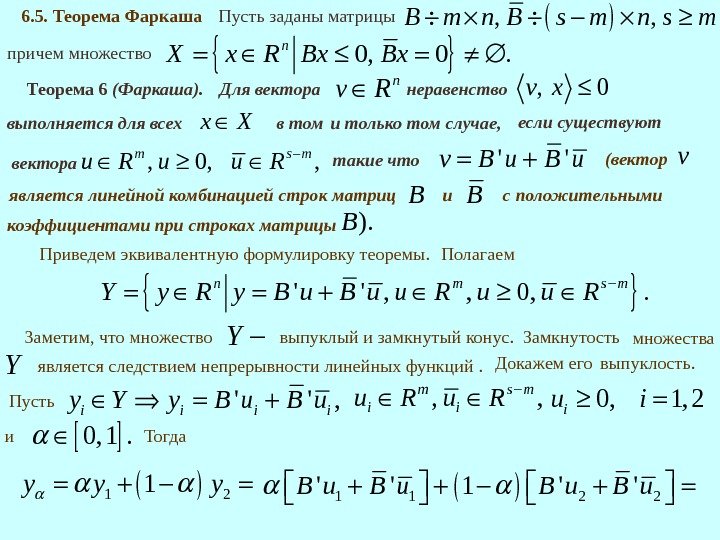







lekciya_19.ppt
- Размер: 1,020.5 Кб
- Автор: Progressive Sound
- Количество слайдов: 11
Описание презентации ВЫПУКЛЫЙ АНАЛИЗ ЛЕКЦИЯ 1 9 6. ТЕОРЕМЫ ОБ по слайдам
 ВЫПУКЛЫЙ АНАЛИЗ ЛЕКЦИЯ 1 9 6. ТЕОРЕМЫ ОБ ОТДЕЛИМОСТИ ВЫПУКЛЫХ МНОЖЕСТВ (ПРОДОЛЖЕНИЕ)
ВЫПУКЛЫЙ АНАЛИЗ ЛЕКЦИЯ 1 9 6. ТЕОРЕМЫ ОБ ОТДЕЛИМОСТИ ВЫПУКЛЫХ МНОЖЕСТВ (ПРОДОЛЖЕНИЕ)
 6. ТЕОРЕМЫ ОБ ОТДЕЛИМОСТИ ВЫПУКЛЫХ МНОЖЕСТВ (ПРОДОЛЖЕНИЕ) 6. 5. Теорема Фаркаша
6. ТЕОРЕМЫ ОБ ОТДЕЛИМОСТИ ВЫПУКЛЫХ МНОЖЕСТВ (ПРОДОЛЖЕНИЕ) 6. 5. Теорема Фаркаша
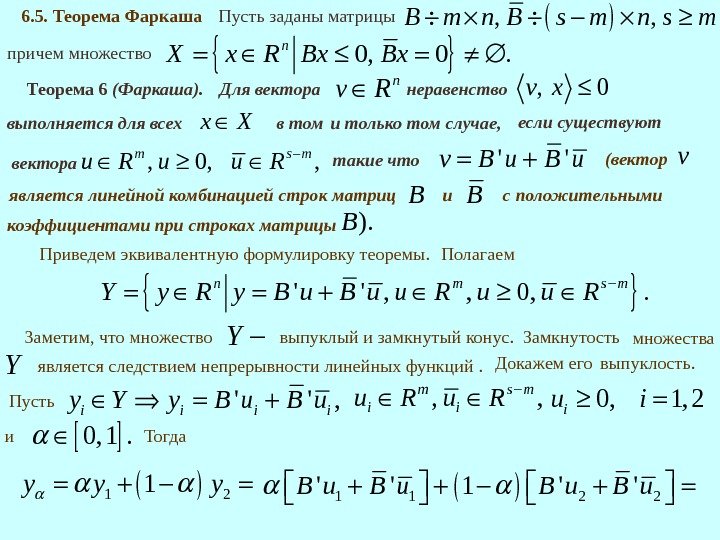 причем множество, , B m n B s m n s m Пусть заданы матрицы 0, 0. n X x R Bx Bx Теорема 6 (Фаркаша). неравенство , 0 v x выполняется для всех x X и только том случае, в том такие что ‘ ‘v B u n v RДля вектора если существуют , 0, , m s m u R u u R вектора 6. 5. Теорема Фаркаша (векторv является линейной комбинацией строк матриц B и. B с положительными коэффициентами при строках матрицы ). B Полагаем. Приведем эквивалентную формулировку теоремы. ‘ ‘ , , 0, . n m s m Y y R y B u u R Заметим, что множество Y выпуклый и замкнутый конус. Замкнутость множества Y является следствием непрерывности линейных функций. Докажем его выпуклость. Пусть ‘ ‘ , i iy Y y B u и 0, 1. Тогда 1 21 y y y , , m s m i iu R 0, 1, 2 iu i 1 1 2 2’ ‘ 1 ‘ ‘B u B u
причем множество, , B m n B s m n s m Пусть заданы матрицы 0, 0. n X x R Bx Bx Теорема 6 (Фаркаша). неравенство , 0 v x выполняется для всех x X и только том случае, в том такие что ‘ ‘v B u n v RДля вектора если существуют , 0, , m s m u R u u R вектора 6. 5. Теорема Фаркаша (векторv является линейной комбинацией строк матриц B и. B с положительными коэффициентами при строках матрицы ). B Полагаем. Приведем эквивалентную формулировку теоремы. ‘ ‘ , , 0, . n m s m Y y R y B u u R Заметим, что множество Y выпуклый и замкнутый конус. Замкнутость множества Y является следствием непрерывности линейных функций. Докажем его выпуклость. Пусть ‘ ‘ , i iy Y y B u и 0, 1. Тогда 1 21 y y y , , m s m i iu R 0, 1, 2 iu i 1 1 2 2’ ‘ 1 ‘ ‘B u B u
 Доказательство. Необходимость. , 0. v x x X v Y 1 1 2 21»»B BBu u u. Bu 1 2 0, 1 2′ 1 m s mu R B u u 6 4 4 7 4 48 Покажем, что множество Y конус. Действительно, пусть0 и y Y ‘ ‘ , , 0, . m s m y B u u R Тогда }}0, ‘ ‘ ms m. RR B u . y Y 0, ‘ ‘ ms m. RR y B u Эквивалентная формулировка теоремы. и для всех Xx справедливо , 0. v x Пусть n v R Требуется доказать, что . v Y Предположим, что. v Y , , , l y l v y Y , , , . l y l v y Y Тогда по , 0 n l R l такой, что теореме 2 существует вектор 0 ‘ ‘. B u Y
Доказательство. Необходимость. , 0. v x x X v Y 1 1 2 21»»B BBu u u. Bu 1 2 0, 1 2′ 1 m s mu R B u u 6 4 4 7 4 48 Покажем, что множество Y конус. Действительно, пусть0 и y Y ‘ ‘ , , 0, . m s m y B u u R Тогда }}0, ‘ ‘ ms m. RR B u . y Y 0, ‘ ‘ ms m. RR y B u Эквивалентная формулировка теоремы. и для всех Xx справедливо , 0. v x Пусть n v R Требуется доказать, что . v Y Предположим, что. v Y , , , l y l v y Y , , , . l y l v y Y Тогда по , 0 n l R l такой, что теореме 2 существует вектор 0 ‘ ‘. B u Y
 Обозначая , c l приходим к неравенству , , , . 1 c y c v y Y , , , . l y l v y Y Покажем, что 0, 0. n c X x R Bx Bx Множество Y конус. 0. y Y Тогда Из (1)следует } , , Y c y c v 0 , , 0. 2 c y c v y Y Неравенство (2) возможно для , 0 y Y только, если , 0. . 3 c y y Y в силу (3) выводим } ‘ ‘ 0 , B uc y , ‘ ‘c B u , , Bc u Для 0 ‘ ‘y Y y B u , 0, m s m u R u u R и всех , , 0 Bc uв проекции на i ю координату 1 1 10, 0, 1, , , 4 m s m j i i j i j. Bc u u i m u R L
Обозначая , c l приходим к неравенству , , , . 1 c y c v y Y , , , . l y l v y Y Покажем, что 0, 0. n c X x R Bx Bx Множество Y конус. 0. y Y Тогда Из (1)следует } , , Y c y c v 0 , , 0. 2 c y c v y Y Неравенство (2) возможно для , 0 y Y только, если , 0. . 3 c y y Y в силу (3) выводим } ‘ ‘ 0 , B uc y , ‘ ‘c B u , , Bc u Для 0 ‘ ‘y Y y B u , 0, m s m u R u u R и всех , , 0 Bc uв проекции на i ю координату 1 1 10, 0, 1, , , 4 m s m j i i j i j. Bc u u i m u R L
 0, 0. Bc Bc следует От противного приходим к 1, , : 0 i i m Bc L или 1, , : 0. j j s m Bc L Тогда выбором 0 i u или , , j j j u sign Bc можно нарушить неравенство (4). 0, 0. n c X x R Bx Bx Доказанные соотношения означают, что 0, 0 Bc Bc По условиям необходимости должно выполняться , 0. c X v c 1 1 10, 0, 1, , , 4 m s m j i i j i j. Bc u u i m u R LПокажем, что из (4) 0 y Y Однако в силу из (1), , , 1 c y c v y Y следует 0 , , c y c v , 0. c v Полученное противоречие доказывает необходимость Достаточность. Пусть ‘ ‘ , , 0, . n m s m v Y y R y B u u R 0 , , c y c v
0, 0. Bc Bc следует От противного приходим к 1, , : 0 i i m Bc L или 1, , : 0. j j s m Bc L Тогда выбором 0 i u или , , j j j u sign Bc можно нарушить неравенство (4). 0, 0. n c X x R Bx Bx Доказанные соотношения означают, что 0, 0 Bc Bc По условиям необходимости должно выполняться , 0. c X v c 1 1 10, 0, 1, , , 4 m s m j i i j i j. Bc u u i m u R LПокажем, что из (4) 0 y Y Однако в силу из (1), , , 1 c y c v y Y следует 0 , , c y c v , 0. c v Полученное противоречие доказывает необходимость Достаточность. Пусть ‘ ‘ , , 0, . n m s m v Y y R y B u u R 0 , , c y c v
 }}00 0 , , 0. u Bx Теорема доказана полностью. Требуется доказать, что , 0 0, 0. n v x x X x R Bx Bx ‘ ‘ , , 0, n m s m v Y y R y B u u R 0 ‘ ‘ 0 , ‘ ‘ , B u x X v x B u x Действительно, Дадим геометрическую интерпретацию теореме Фаркаша для частного случая 2, 2. s m n Тогда матрица 11 12 21 22 b b B b b имеет размера 2 2 0 n X x R Bx 11 12 12 21 22 2 0. b b x x R b b x Обозначим через 11 21 1 2 12 22 , b b b столбцы матрицы. B и Тогда
}}00 0 , , 0. u Bx Теорема доказана полностью. Требуется доказать, что , 0 0, 0. n v x x X x R Bx Bx ‘ ‘ , , 0, n m s m v Y y R y B u u R 0 ‘ ‘ 0 , ‘ ‘ , B u x X v x B u x Действительно, Дадим геометрическую интерпретацию теореме Фаркаша для частного случая 2, 2. s m n Тогда матрица 11 12 21 22 b b B b b имеет размера 2 2 0 n X x R Bx 11 12 12 21 22 2 0. b b x x R b b x Обозначим через 11 21 1 2 12 22 , b b b столбцы матрицы. B и Тогда
 X 1 B 2 B 090 v 090 Теорема 5 ( Фаркаша). в том и только том случае, Неравенство 0, xv выполняется для всех x X 12 1 2 2 , 0, 0, u u R u u u если существует вектор что 1 1 2 2′. v B u b u 1 1 1 2 2 2 , 0, , 0. nx x X x R b b x x 12 2 , v v R v Пусть
X 1 B 2 B 090 v 090 Теорема 5 ( Фаркаша). в том и только том случае, Неравенство 0, xv выполняется для всех x X 12 1 2 2 , 0, 0, u u R u u u если существует вектор что 1 1 2 2′. v B u b u 1 1 1 2 2 2 , 0, , 0. nx x X x R b b x x 12 2 , v v R v Пусть
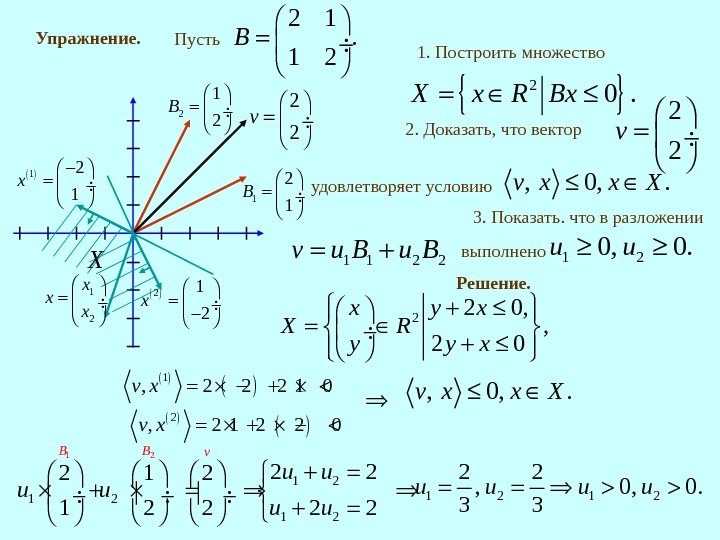
 Упражнение. Пусть2 1. 1 2 B 1. Построить множество 2 0. X x R Bx 2. Доказать, что вектор 2 2 v удовлетворяет условию , 0, . v x x X 3. Показать. что в разложении 1 1 2 2 v u B выполнено 1 20, 0. u u Решение. 22 0, , 2 0 x y x X R y y x 1 2 1 B 2 1 2 B X 12 1 x 21 2 x 2 2 v 1 2 x x x 1 , 2 2 2 1 0 v x 2, 2 1 2 2 0 v x , 0, . v x x X 1 2 1 2 2 22 1 2 2 B Bv u u u 1 2 2 2 , 0, 0. 3 3 u u
Упражнение. Пусть2 1. 1 2 B 1. Построить множество 2 0. X x R Bx 2. Доказать, что вектор 2 2 v удовлетворяет условию , 0, . v x x X 3. Показать. что в разложении 1 1 2 2 v u B выполнено 1 20, 0. u u Решение. 22 0, , 2 0 x y x X R y y x 1 2 1 B 2 1 2 B X 12 1 x 21 2 x 2 2 v 1 2 x x x 1 , 2 2 2 1 0 v x 2, 2 1 2 2 0 v x , 0, . v x x X 1 2 1 2 2 22 1 2 2 B Bv u u u 1 2 2 2 , 0, 0. 3 3 u u



