ВЫПУКЛЫЙ АНАЛИЗ ЛЕКЦИЯ 1 5 4. СВЯЗЬ МЕЖДУ






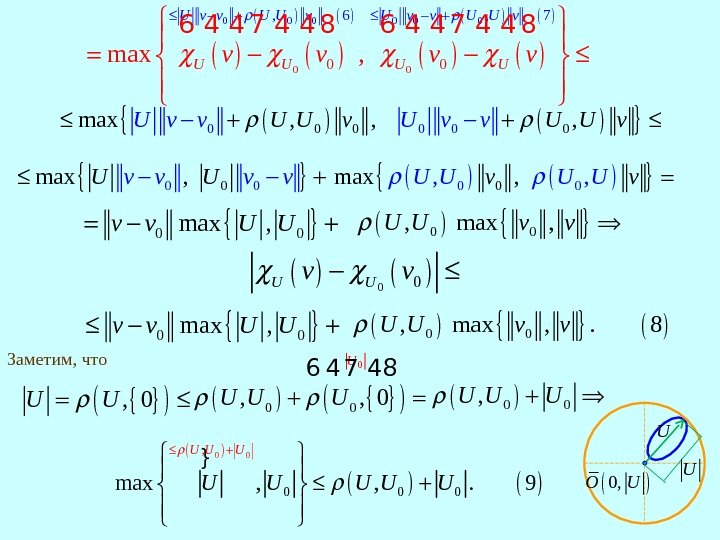
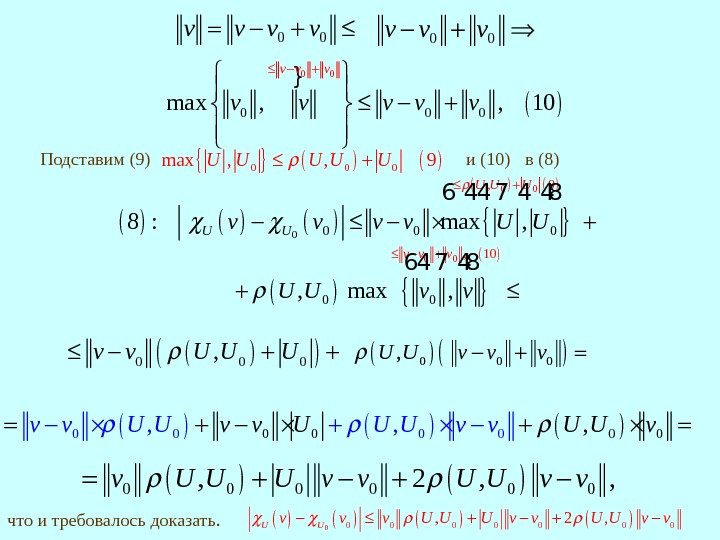




lekciya_15.ppt
- Размер: 1,000.5 Кб
- Автор: Progressive Sound
- Количество слайдов: 11
Описание презентации ВЫПУКЛЫЙ АНАЛИЗ ЛЕКЦИЯ 1 5 4. СВЯЗЬ МЕЖДУ по слайдам
 ВЫПУКЛЫЙ АНАЛИЗ ЛЕКЦИЯ 1 5 4. СВЯЗЬ МЕЖДУ ВЫПУКЛЫМИ ФУНКЦИЯМИ И ВЫПУКЛЫМИ МНОЖЕСТВАМИ
ВЫПУКЛЫЙ АНАЛИЗ ЛЕКЦИЯ 1 5 4. СВЯЗЬ МЕЖДУ ВЫПУКЛЫМИ ФУНКЦИЯМИ И ВЫПУКЛЫМИ МНОЖЕСТВАМИ
 4. СВЯЗЬ МЕЖДУ ВЫПУКЛЫМИ ФУНКЦИЯМИ И ВЫПУКЛЫМИ МНОЖЕСТВАМИ (ПРОДОЛЖЕНИЕ) 4. 3. Опорная функция подмножества пространства (продолжение) . n R 4. 4. Опорные функции выпуклых оболочек подмножеств пространства. n R
4. СВЯЗЬ МЕЖДУ ВЫПУКЛЫМИ ФУНКЦИЯМИ И ВЫПУКЛЫМИ МНОЖЕСТВАМИ (ПРОДОЛЖЕНИЕ) 4. 3. Опорная функция подмножества пространства (продолжение) . n R 4. 4. Опорные функции выпуклых оболочек подмножеств пространства. n R
 Свойство 7. Пусть n RUU 0, компактные множества и 0, . n v v R Тогда 0 0, v U U U v v 0 0 U Uv v где расстояние Хаусдорфа между множествами U и 0; U Доказательство. 0 02 , , U U v v 0 0 min 0 0, , 0, R U U O R 0, U U 0 0 max u U U u модуль множества 0. U 4. 3. Опорная функция подмножества пространства Из свойства 2 1 2 U U Uv v опорных функций следует 0 0 U Uvvvv 0 0 U Uv v v Оценим каждое из слагаемых в правой части (3). 0 0. 3 U U Uv v . n R (продолжение)
Свойство 7. Пусть n RUU 0, компактные множества и 0, . n v v R Тогда 0 0, v U U U v v 0 0 U Uv v где расстояние Хаусдорфа между множествами U и 0; U Доказательство. 0 02 , , U U v v 0 0 min 0 0, , 0, R U U O R 0, U U 0 0 max u U U u модуль множества 0. U 4. 3. Опорная функция подмножества пространства Из свойства 2 1 2 U U Uv v опорных функций следует 0 0 U Uvvvv 0 0 U Uv v v Оценим каждое из слагаемых в правой части (3). 0 0. 3 U U Uv v . n R (продолжение)
 0 0. 4 Uv v U v v 0 0 : 0 0, шар U v v UO Uv v 6 44 7 4 48 0 00, , . U O U UПо определению расстояния Хаусдорфа выводим Тогда 0 U v v 0, 0 U U 0, O U Из вложения 0, U O U по свойству 6 следует неравенство 0 00 0 06 4 , , U U O Uсвойство Uv v 0 0 0 0, , , 4 U O U U U v свой тв Uс о v v 6 4 4 7 4 48 00 0 0, Uv U U v 00 0 0 0, . 5 U Uv v U U v
0 0. 4 Uv v U v v 0 0 : 0 0, шар U v v UO Uv v 6 44 7 4 48 0 00, , . U O U UПо определению расстояния Хаусдорфа выводим Тогда 0 U v v 0, 0 U U 0, O U Из вложения 0, U O U по свойству 6 следует неравенство 0 00 0 06 4 , , U U O Uсвойство Uv v 0 0 0 0, , , 4 U O U U U v свой тв Uс о v v 6 4 4 7 4 48 00 0 0, Uv U U v 00 0 0 0, . 5 U Uv v U U v
 Подставим полученные неравенства (4) и (5) в (3). 0 0, Uv U U v 0 Uv U v v 0 0 000 0 5 , 0 4 3 U U v v v 00 0 0 0, . 6 U Uv v U U v Меняя местами n RUU 0, и 0, , n v v R получим 00 0 0 0, . 7 U Uv v U U v Из (6) и (7) в силу очевидного равенства 0 0 U Uv v 0 0 0 00 0 , 6 , 7 max , U U v v U U v v 6 4 4 7 4 4 8 1 max , x x R выводим
Подставим полученные неравенства (4) и (5) в (3). 0 0, Uv U U v 0 Uv U v v 0 0 000 0 5 , 0 4 3 U U v v v 00 0 0 0, . 6 U Uv v U U v Меняя местами n RUU 0, и 0, , n v v R получим 00 0 0 0, . 7 U Uv v U U v Из (6) и (7) в силу очевидного равенства 0 0 U Uv v 0 0 0 00 0 , 6 , 7 max , U U v v U U v v 6 4 4 7 4 4 8 1 max , x x R выводим
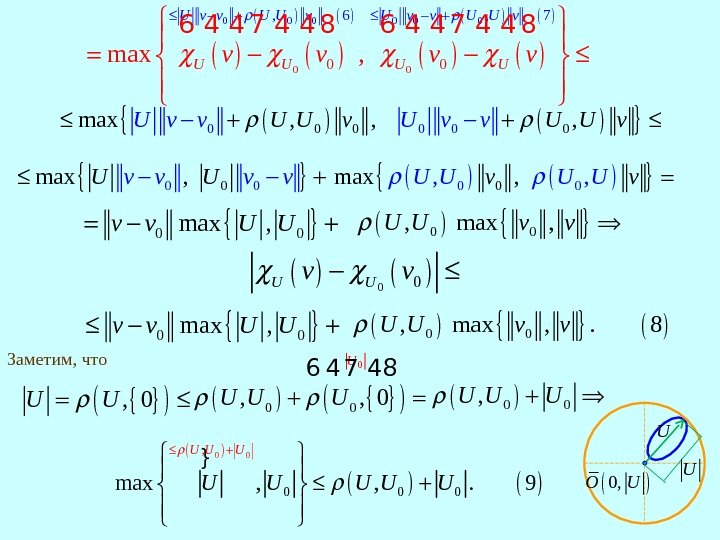 0 00 000 max , , , U v v. U U v 000 max , v v v. U Uv 00 0 max , , , Uv. U U Uv 0 0 0 00 0 , 6 , 7 max , U U v v U U v v 6 4 4 7 4 4 8 0 0 max , v v U U 0 0, max , U U v v 00 U U v v 0 0 max , v v U U 0 0, max , . 8 U U v v , 0 U U Заметим, что U U 0, O U 0 0 0, , 0 UU U U 6 4 7 48 0 0, U U U } 0 0 0 , max , , . 9 U U U U
0 00 000 max , , , U v v. U U v 000 max , v v v. U Uv 00 0 max , , , Uv. U U Uv 0 0 0 00 0 , 6 , 7 max , U U v v U U v v 6 4 4 7 4 4 8 0 0 max , v v U U 0 0, max , U U v v 00 U U v v 0 0 max , v v U U 0 0, max , . 8 U U v v , 0 U U Заметим, что U U 0, O U 0 0 0, , 0 UU U U 6 4 7 48 0 0, U U U } 0 0 0 , max , , . 9 U U U U
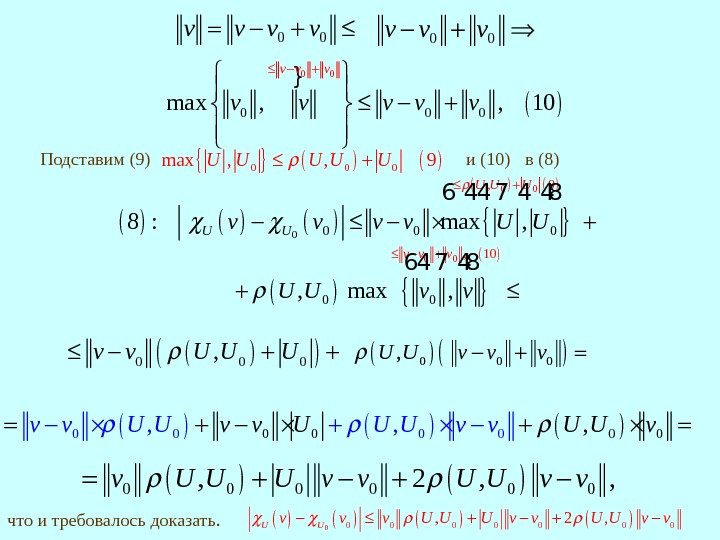 0 0 v v } 0 0 0 max , , 10 v v v v 0 0 v v v Подставим (9) 0 0 0 max , , 9 U U U и ( 10 ) 0 0 0 , 9 8 : max , U U U v v U U 6 44 7 4 48 в (8) 0 0 , 10 , max , v v v U U v v 64 7 48 0 0 0, v v U U U 0 0 0, U U v v v 0 00 0 0 0, , , v v U U U vv. U v 0 0 0, 2 , , v U U U v v что и требовалось доказать. 00 0 0 0, 2 , U Uv v v U U U v v
0 0 v v } 0 0 0 max , , 10 v v v v 0 0 v v v Подставим (9) 0 0 0 max , , 9 U U U и ( 10 ) 0 0 0 , 9 8 : max , U U U v v U U 6 44 7 4 48 в (8) 0 0 , 10 , max , v v v U U v v 64 7 48 0 0 0, v v U U U 0 0 0, U U v v v 0 00 0 0 0, , , v v U U U vv. U v 0 0 0, 2 , , v U U U v v что и требовалось доказать. 00 0 0 0, 2 , U Uv v v U U U v v
 4. 4. Опорные функции выпуклых оболочек подмножеств пространства . n R Пусть n. RU компактное множество. Ранее было доказано, что множество co. U также компактно. Свойство 1. Пусть n RU компактное множество. , . n U co. Uv v v R Доказательство. Из вложения Uco. U следует , . 1 n U co. Uv v v R Докажем неравенство в другую сторону. Тогда Имеем Следствие. Опорная функция v. U непрерывна по совокупности переменных nn. RURv, и, следовательно, по каждому из них в отдельности. Установим некоторые свойства опорных функций выпуклых оболочек компактных подмножеств пространства . n R
4. 4. Опорные функции выпуклых оболочек подмножеств пространства . n R Пусть n. RU компактное множество. Ранее было доказано, что множество co. U также компактно. Свойство 1. Пусть n RU компактное множество. , . n U co. Uv v v R Доказательство. Из вложения Uco. U следует , . 1 n U co. Uv v v R Докажем неравенство в другую сторону. Тогда Имеем Следствие. Опорная функция v. U непрерывна по совокупности переменных nn. RURv, и, следовательно, по каждому из них в отдельности. Установим некоторые свойства опорных функций выпуклых оболочек компактных подмножеств пространства . n R
 } 1 11, 0, 1, , 1 1 max n i i i n U i i i n v L 1 11 0, 1, , 1 1 1, max , in i i U v n i i n u U i u v L 6 4 7 48 1 1 1 0, 1, , 1 1 1, maxi n i Uv L 1 1, , 0, 1, 1 max , n i i i n i i co. U u u u U u c i o. U n v u v L 1 1 1 0, , 1 1, , 1, max , 1 max , n i i i n U i i u i n i iu Ui i n u v L 6 4 7 4 8 1 1 1 , 0, 1 1, , 1, 1 max , i i n i i u U i i n u v L Uv , . 2 n co. U Uv v v R Из (1) , 1 n U co. Uv v v R и (2) следует справедливость доказываемого свойства.
} 1 11, 0, 1, , 1 1 max n i i i n U i i i n v L 1 11 0, 1, , 1 1 1, max , in i i U v n i i n u U i u v L 6 4 7 48 1 1 1 0, 1, , 1 1 1, maxi n i Uv L 1 1, , 0, 1, 1 max , n i i i n i i co. U u u u U u c i o. U n v u v L 1 1 1 0, , 1 1, , 1, max , 1 max , n i i i n U i i u i n i iu Ui i n u v L 6 4 7 4 8 1 1 1 , 0, 1 1, , 1, 1 max , i i n i i u U i i n u v L Uv , . 2 n co. U Uv v v R Из (1) , 1 n U co. Uv v v R и (2) следует справедливость доказываемого свойства.
 Упражнение. Найти опорную функцию множества 2 2, 0, 0 x U x y y x y 0, 0 O 1, 0 B 0, 2 A U Решение. 0 1 0 , , 0 0 2 U co % 0 1 0 , , , 0 0 2 U % max , UUu U v v v u %% 1 1 1 2 2 2 0 1 0 max , , 0 0 2 v v v 1 2 max 0, , 2 , v v Для всех 2 v R имеем и вычислить ее в точке 3. 2 v max 0, 3, 2 2 4. Uv
Упражнение. Найти опорную функцию множества 2 2, 0, 0 x U x y y x y 0, 0 O 1, 0 B 0, 2 A U Решение. 0 1 0 , , 0 0 2 U co % 0 1 0 , , , 0 0 2 U % max , UUu U v v v u %% 1 1 1 2 2 2 0 1 0 max , , 0 0 2 v v v 1 2 max 0, , 2 , v v Для всех 2 v R имеем и вычислить ее в точке 3. 2 v max 0, 3, 2 2 4. Uv


