Выполнили Рыбакова Т Д Степанова М С

Выполнили: Рыбакова Т. Д. , Степанова М. С.

Во многих областях практики возникают своеобразные задачи оптимизации решений, для которых характерны следующие черты: показатель эффективности W представляет собой линейную функцию от элементов решения x 1, x 2, …; ограничительные условия, налагаемые на возможные решения, имеют вид линейных равенств или неравенств. Такие задачи принято называть задачами линейного программирования.

Имеются какие-то ресурсы (сырье, рабочая сила, оборудование ): R 1, R 2, …, Rm в количествах соответственно b 1, b 2, …, bm единиц. С помощью этих ресурсов могут производится товары: Т 1, Т 2, …, Тn Для производства одной единицы товара Tj необходимо aij единиц ресурса Ri (i=1, 2, …, m; j=1, 2, …, n ). Каждая единица ресурса Ri стоит di рублей (i=1, 2, …, m). Каждая единица товара Tj может быть реализована по цене сj(j=1, 2, …, n).

По каждому виду товара количество произведенных единиц ограничивается спросом: известно, что рынок не может поглотить более чем kj единиц товара Tj (j=1, 2, …, n).

Запишем условия задачи. Обозначим x 1, x 2, …, xn количество товаров Т 1, Т 2, …, Тn, которые мы запланируем к производству. Условия спроса налагают на эти величины ограничения: x 1<=k 1; x 2<=k 2; … ; xn<=kn

Ресурсов должно хватить, отсюда возникают ограничения: a 11 x 1 +a 12 x 2+ …+ a 1 nxn <=b 1 a 21 x 1 + a 22 x 2+…+ a 2 nxn<=b 2 ………… am 1 x 1+am 2 x 2+…+amnxn<=bm Эти условия можно короче записать в виде:

Выразим прибыль L в зависимости от элементов решения x 1, x 2, …, xn Себестоимость sj единицы товара Tj равна Sj= a 1 jd 1 +a 2 jd 2+ …+ amjdm или sj = (j=1, 2, …, n ) Вычислив по этой формуле себестоимость единицы каждого товара, получим ряд значений: s 1, s 2, …, sn

Чистая прибыль qj, получаемая от реализации одной единицы товара Tj, равна разнице между ее продажной ценой cj и себестоимостью sj : qj=cj-sj (j=1, 2, …, n ) По этой формуле получаем чистые прибыли на единицу для всех товаров: q 1, q 2, …, qn Общая чистая прибыль от реализации всех товаров будет L= q 1 x 1 +q 2 x 2+ …+ qnxn или

Постановка задачи: Выбрать такие неотрицательные значения переменных x 1, x 2, …, xn, которые удовлетворяют линейным неравенствам и обращают в максимум линейную функцию этих переменных. Решением задачи: (точкой максимума) называется такая точка, координаты которой удовлетворяют всем ограничениям; и при этом значение целевой функции максимально. Система ограничений формирует область допустимых решений (ОДР), т. е. множество точек, координаты которых удовлетворяют всем ограничениям. Именно среди них нужно искать точку максимума.

Это замкнутый выпуклый многоугольник. Геометрический смысл задачи линейного программирования состоит в том, чтобы, не выходя за пределы допустимой области, найти точку на линии уровня с наибольшим значением. Решение задачи ЛП достигается в вершине ОДР.

ГРАФИЧЕСКИЙ СПОСОБ

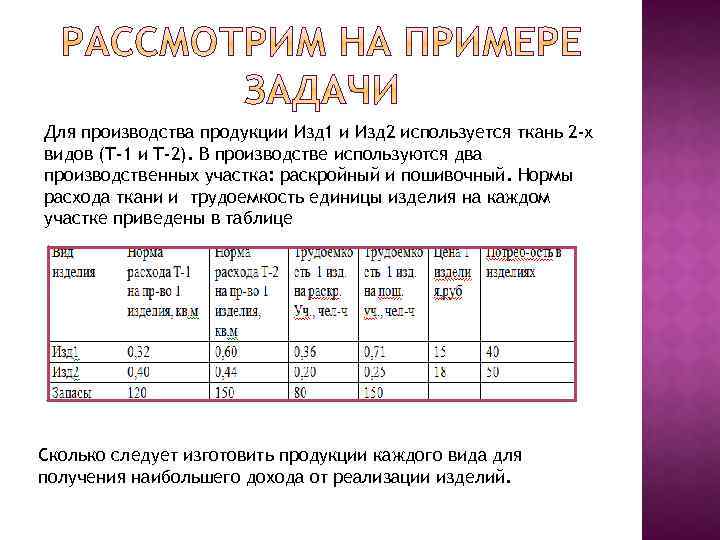
Для производства продукции Изд 1 и Изд 2 используется ткань 2 -х видов (Т-1 и Т-2). В производстве используются два производственных участка: раскройный и пошивочный. Нормы расхода ткани и трудоемкость единицы изделия на каждом участке приведены в таблице Сколько следует изготовить продукции каждого вида для получения наибольшего дохода от реализации изделий.

Дана целевая функция: Определяем ограничения по условию задачи:

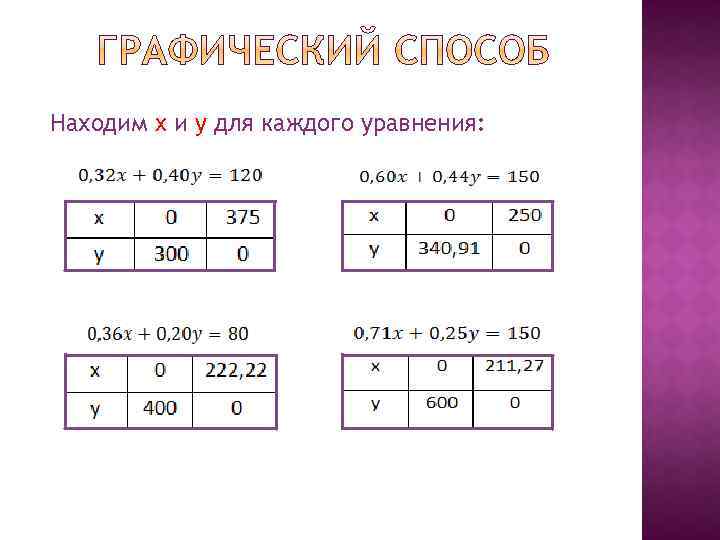
Находим x и y для каждого уравнения:

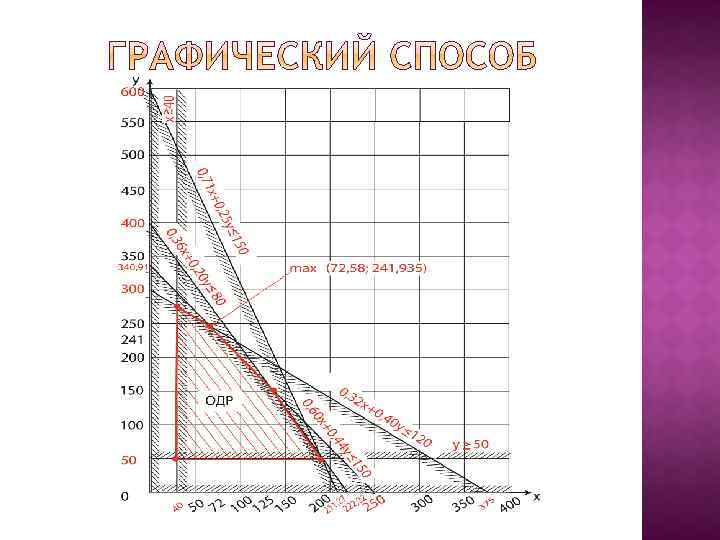
Что требуется для того чтобы найти ОДР: Построить прямые, заданных уравнений Выбрать любую точку на этой прямой, и подставить ее значения в уравнение Решить его, и отметить штриховкой (если решение удовлетворяет условие уравнения, то штриховка будет во внутрь, иначе в обратную сторону) Отметить пределы допустимой области И найти максимальную точку(значения должны совпасть со значениями полученными другим путем решения задачи)

РЕШЕНИЕ СИСТЕМЫ УРАВНЕНИЙ

Выберем из системы два уравнения и решим их:

ПОИСК РЕШЕНИЯ (EXCEL)

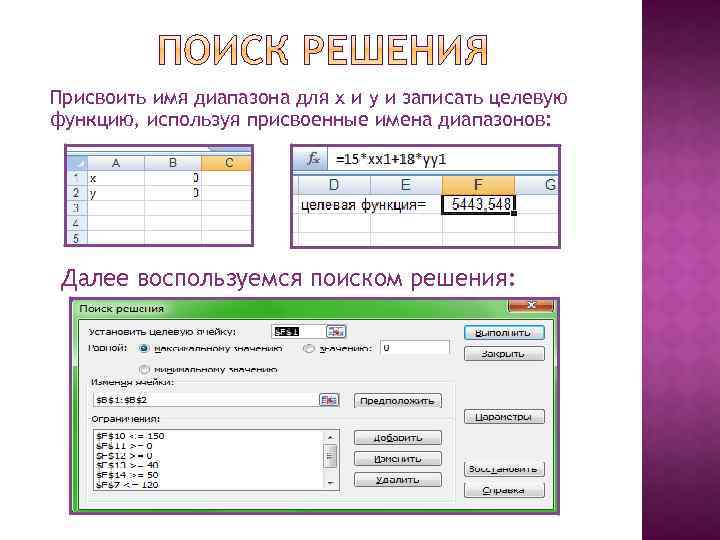
Присвоить имя диапазона для x и y и записать целевую функцию, используя присвоенные имена диапазонов: Далее воспользуемся поиском решения:

Во вкладке поиск решения задаем ограничения, заданные условием: Нажимаем кнопку выполнить:

Напротив x и y, вместо значения 0, появится ответ: Ответ должен совпасть с ответами других способов решения