Выполнили Калинцева А Крехалева Н Цель Систематизировать

Выполнили: Калинцева А. Крехалева Н.

Цель: Систематизировать и обобщить знания по теме многогранники. Задачи: Проанализировать литературу по данной теме; Познакомиться с такими понятиями, как центр симметрии, ось симметрии и плоскость симметрии; Оформить работу с использованием полученных знаний.

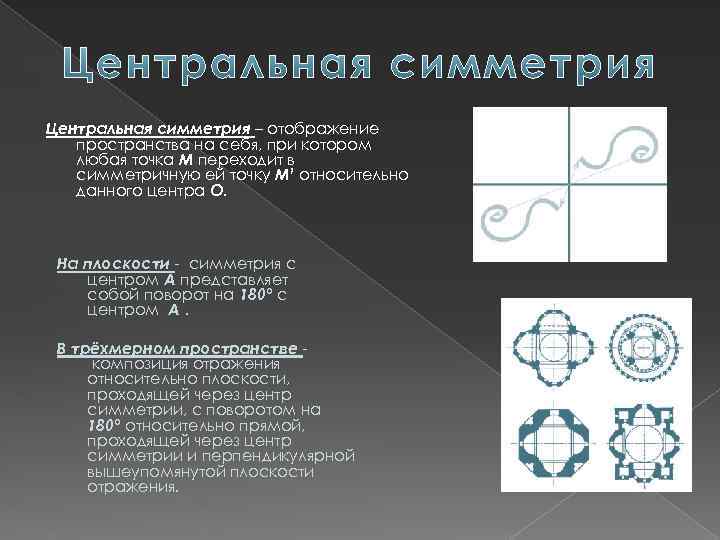Центральная симметрия – отображение пространства на себя, при котором любая точка М переходит в симметричную ей точку М¹ относительно данного центра О. На плоскости - симметрия с центром A представляет собой поворот на 180° с центром A. В трёхмерном пространстве композиция отражения относительно плоскости, проходящей через центр симметрии, с поворотом на 180° относительно прямой, проходящей через центр симметрии и перпендикулярной вышеупомянутой плоскости отражения.

В пространстве

Осевая симметрия с осью а – отображение пространства на себя, при котором любая точка М переходит в симметричную ей точку М¹ относительно оси а. На плоскости – осевая симметрия – движение плоскости, у которого множество неподвижных точек – прямая, является осевой симметрией. В пространстве – под осевой симметрией понимают вращательную симметрию относительно поворотов вокруг прямой.

В пространстве

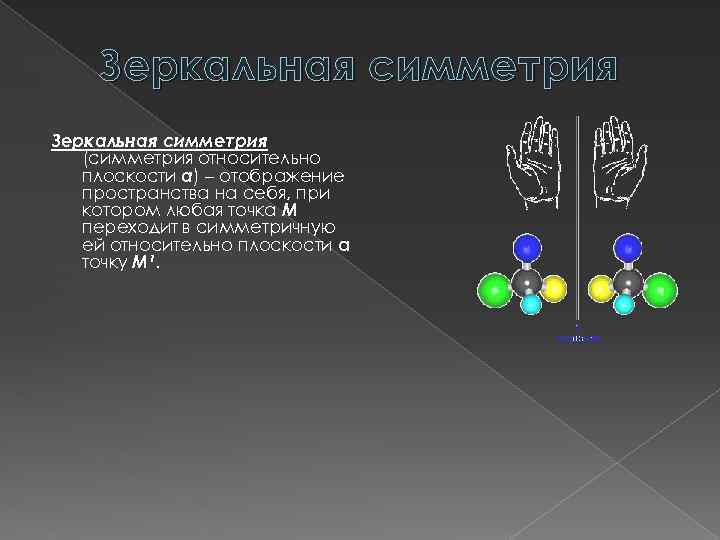Зеркальная симметрия (симметрия относительно плоскости а) – отображение пространства на себя, при котором любая точка М переходит в симметричную ей относительно плоскости а точку М¹.

Параллельный перенос Паралле льный перено с ― частный случай движения, при котором все точки пространства перемещаются в одном и том же направлении на одно и то же расстояние. На плоскости параллельный перенос выражается аналитически в прямоугольной системе координат (x, y) при помощи Где вектор В пространстве - такое преобразование, при котором произвольная точка (x; y; z) фигуры переходит в точку (x+a; y+b; z+c), где числа a, b, с одни и те же для всех точек (x; y; z).

ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС И ЕГО СВОЙСТВА В ПРОСТРАНСТВЕ Параллельный перенос есть движение. При параллельном переносе точки смещаются по параллельным прямым на одно и то же расстояние. При параллельном переносе каждая прямая переходит в параллельную ей прямую или в себя. Каковы бы ни были точки A и A`, существует единственный параллельный перенос, при котором точка A переходит в точку A`. При параллельном переносе в пространстве каждая плоскость переходит либо в себя, либо в параллельную ей плоскость.

Гомотетия преобразование плоскости или пространства, при котором каждой точке М ставится в соответствие точка М , лежащая на ОМ, О фиксированная точка, причем отношение ОМ : ОМ =k (коэффициент гомотетии) одно и то же для всех точек М, отличных от О. При гомотетии каждая фигура переходит в подобную

Симметрия среди чудес света

П и р а м и д а х е о п с а 1. 2. 3. 4. Время создания: 2550 г. до н. э. ; Место: Гиза (Египет); Назначение: гробница фараона Хеопса; Особенности: единственное из чудес света, сохранившееся до наших дней.

Симметрия Осевая симметрия Зеркальная симметрия

В и с я ч и е с а д ы 1. 2. с Е м и Р а м и д ы 3. 4. 5. Время создания: 600 г. до н. э. ; Место: Вавилон (Ирак); Разрушение: после первого столетия до н. э. ; Причина разрушения: землетрясение; Особенности: были созданы для жены царя Навуходоносора 2 го.

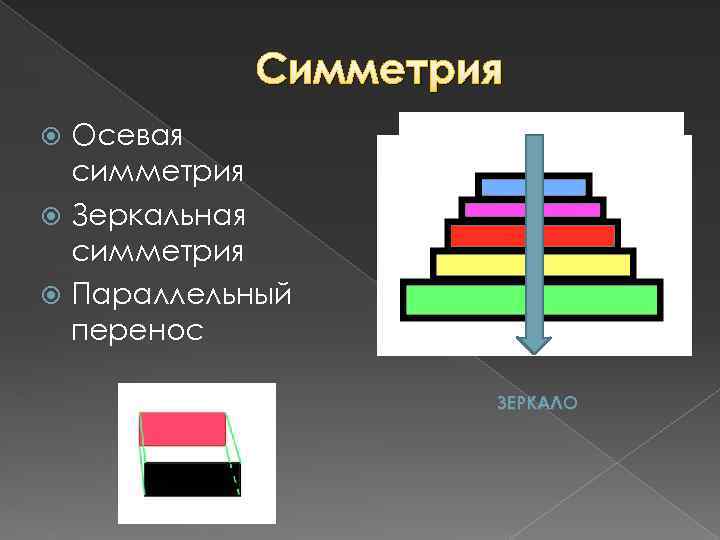Симметрия Осевая симметрия Зеркальная симметрия Параллельный перенос ЗЕРКАЛО

Х р а м а р т е м и д ы 1. 2. В 3. э 4. Ф е с е Время создания: 550 г. до н. э. ; Место: Эфес (Турция); Разрушение: 370 г. до н. э. , 356 г. до н. э. (Геростратом), 262 г. н. э. (готами); Назначение: в честь богини Артемиды.

Симметрия Зеркальная симметрия Параллельный перенос зеркало

С т а т в у я О 1. 2. 3. 4. Л з И М е П в И с и а 5. Время создания: 435 г. до н. э. ; Место: Олимпия (Греция); Разрушение: 5 -6 вв. ; Причина разрушения: сгорела в Константинополе во время пожара на Ипподроме 5 в. ; Назначение: храмовая статуя в храме Зевса в Олимпии.

Асимметрия Асимметри я (греч. ) — нарушение симметрии, соразмерности или её отсутсвие. Асимметрия в искусстве Как художественный приём, асимметрия придаёт динамику, разнообразие произведению искусства (например, абарокко, рококо, романтизме), вносит элементы непринуждённости, естественной случайности (импрессионизм), причудливость (модерн). В архитектуре асимметричность может обуславливаться функциональным назначением зданий.

М а в З о л е й в 1. 2. Г А Л И К А Р Н А С Е 3. 4. 5. Время создания: 351 г. до н. э. ; Место: Галикарнас (на юго-западе Турции); Разрушение: 1494 г. ; Причина разрушение: землетрясение; Назначение: надгробный памятник карийского правителя Мавсола его женой – царицей Артемисией.

Симметрия Зеркальная симметрия Параллельный перенос Гомотетия зеркало

К о л о с с р а д о с с к и й 1. 2. 3. 4. 5. Время создания: между 292 и 280 гг. до н. э. ; Место: Родос (Греция); Разрушение: 224 или 226 г. до н. э. ; бронзовый корпус был демонтирован в 654 г. н. э. ; Причина разрушения: землетрясение; Назначение: был установлен скульптором Харесом для увековечивания памяти о победе Родоса над Деметрием Полиоркетом в 304 г. до н. э.

Симметрия Зеркальная симметрия ЗЕРКАЛО

А 1. л 2. е к 3. с а н 4. д р 5. и й с к М и А й Я К Время создания: 2 й в. до н. э. ; Место: Александрия (Египет); Разрушение: 303 г. до н. э. – 1480 г. н. э. Причина разрушения: землетрясение; Назначение: для судоходства.

СИММЕТРИЯ Осевая симметрия Зеркальная симметрия Гомотетия ЗЕРКАЛО

Симметрия на плоскости

Квадрат • Прямоугольник с равными сторонами; • Ромб, у которого все углы прямые. Свойства квадрата: • Противоположные стороны равны и параллельны; • Все углы прямые; • Диагонали равны; взаимно перпендикулярны, точкой пересечения делятся пополам и делят пополам углы квадрата; • Точка пересечения диагоналей – центр симметрии, центр вписанной и описанной окружности; • Квадрат имеет 4 оси симметрии. Формулы: • Радиус вписанной окружности квадрата равен – • Радиус описанной окружности квадрата равен – • периметр квадрата равен – • площадь равна - S = t 2 = 2 R 2 = 4 r 2 • диагональ равна -

Правильный треугольник • Это правильный многоугольник с тремя сторонами. • Свойства правильного треугольника: • Все его стороны равны; • Все углы его равны ; • Около него можно описать окружность, и притом только одну; • В него можно вписать окружность, и притом только одну. Формулы: • Радиус вписанной окружности • Радиус описанной окружности – • Периметр – • Высоты, медианы и биссектрисы – • Площадь -

Правильный шестиугольник • это правильный многоугольник с шестью сторонами. Свойства: • Особенность правильного шестиугольника — равенство его стороны и радиуса описанно й окружности (R = t); • Все углы равны 120°; • Шестиугольники замощают плоскость (то есть могут заполнять плоскость без пробелов и наложений). Формулы: • Радиус вписанной окружности – • Периметр – • Площадь –

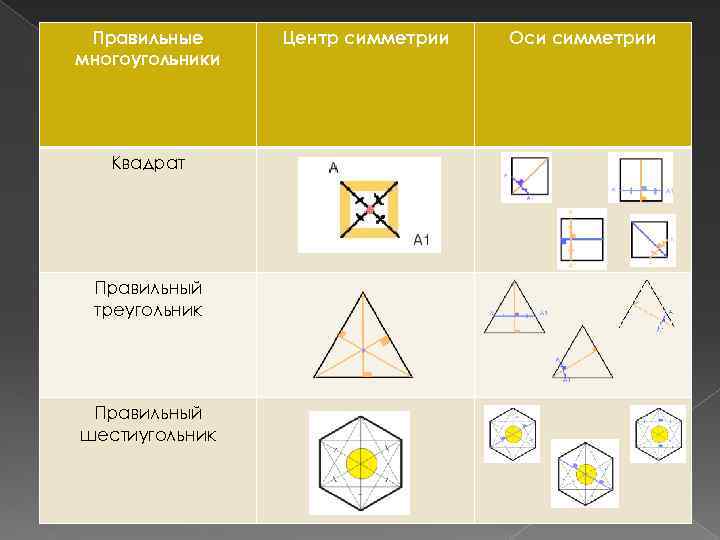Правильные многоугольники Квадрат Правильный треугольник Правильный шестиугольник Центр симметрии Оси симметрии

Симметрия в пространстве

Куб (земля) Куб – прямоугольный параллелепипед с равными измерениями. • Свойства куба: • В куб можно вписать тетраэдр двумя способами; • В куб можно вписать октаэдр, притом все шесть вершин октаэдра будут совмещены с центрами шести граней куба; • Куб можно вписать в октаэдр, притом все восемь вершин куба будут расположены в центрах восьми граней октаэдра; • В куб можно вписать икосаэдр; • Все грани куба – квадраты; • У куба 8 вершин, 12 рёбер, 6 граней. Формулы: • диагональ куба • объём – • Площадь полной поверхности – • Радиус вписанной сферы – • Ребро куба • Радиус описанной сферы –

Правильный тетраэдр (огонь) Правильный тетраэдр – тетраэдр, у которого все грани – равносторонние треугольники. • Свойства: • Каждая его вершина является вершиной трех треугольников, а значит, сумма плоских углов при каждой вершине будет равна 180º. • В правильный тетраэдр можно вписать октаэдр; • Правильный тетраэдр можно вписать в куб двумя способами; • Правильный тетраэдр можно вписать в икосаэдр, притом, четыре вершины тетраэдра будут совмещены с четырьмя вершинами икосаэдра; • У тетраэдра 4 вершины, 6 рёбер, 4 грани; • Не имеет центр симметрии. Формулы: • Площадь поверхности – • Объём • Высота – • Радиус вписанной сферы – • Радиус описанной сферы -

Октаэдр (воздух) Правильный выпуклый многогранник, восемь граней которого являются равносторонними треугольниками. • Свойства октаэдра: • Имеет 8 граней, 12 рёбер, 6 вершин; • Каждая вершина октаэдра является вершиной четырёх треугольников. Следовательно, сумма плоских углов при каждой вершине – 240°; • Все рёбра равны; • Имеет центр симметрии, несколько осей и плоскостей симметрии. • Формулы: • Площадь поверхности – • Объём – • Радиус описанной сферы – • Радиус вписанной сферы -

Икосаэдр (Вода) • Многогранник с двадцатью гранями, каждая из которых является равносторонним треугольником. • Свойства икосаэдра: • Имеет 20 граней, 12 вершин, 30 рёбер; • Имеет 59 звёздчатых форм; • Икосаэдр можно вписать в куб; • В икосаэдр может быть вписан тетраэдр; • Икосаэдр можно вписать в додекаэдр; • Усечённый икосаэдр может быть получен срезанием 12 вершин с образованием граней в виде правильных пятиугольников. • Формулы: • Площадь – • Объём – • Радиус вписанной сферы – • Радиус описанной сферы -

Додекаэдр (Вселенная) • Правильный многогранник, составленный из двенадцати правильных пятиугольников. • Свойства: • Додекаэдр имеет 12 граней, 30 рёбер и 20 вершин; • Додекаэдр имеет центр симметрии и 15 осей симметрии; • Составлен из 20 правильных пятиугольников; • Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников. Следовательно, сумма плоских углов при каждой вершине равна 324. • Формулы: • Площадь поверхности – • Объём – • Радиус описанной сферы – • Радиус вписанной сферы -

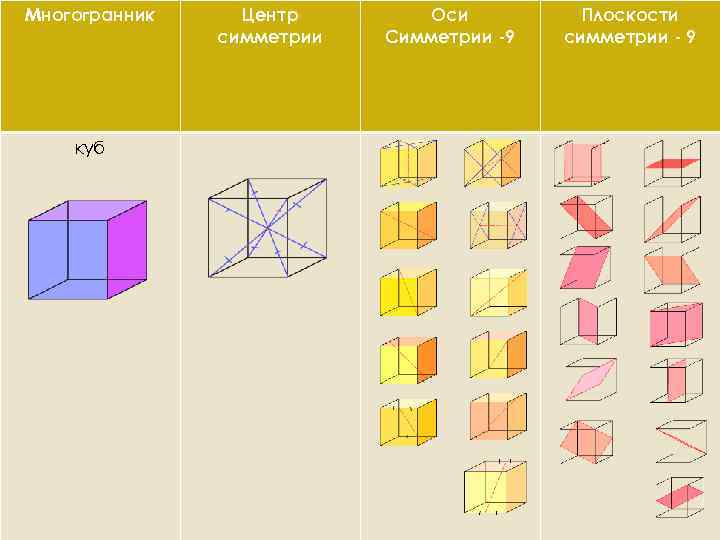Многогранник куб Центр симметрии Оси Симметрии -9 Плоскости симметрии - 9

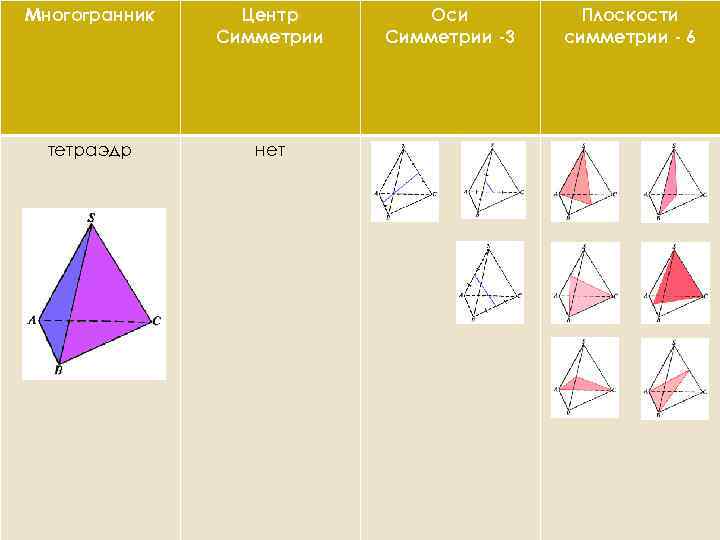Многогранник Центр Симметрии тетраэдр нет Оси Симметрии -3 Плоскости симметрии - 6

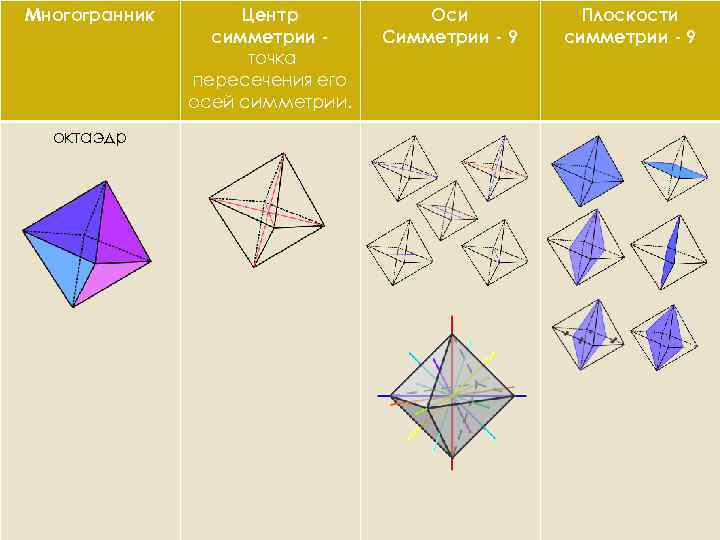Многогранник октаэдр Центр симметрии точка пересечения его осей симметрии. Оси Симметрии - 9 Плоскости симметрии - 9