Выполнила студентка группы ДЭЭ 110 Пенкина Анна

Выполнила студентка группы ДЭЭ 110: Пенкина Анна

Таблица истинности — это таблица, описывающая логическую функцию, в левой части которой записывается набор аргументов, а в правой части - соответствующие значения логической функции. Логическая функция - это функция, в которой переменные принимают только два значения: логическая единица или логический ноль. Истинность или ложность сложных суждений представляет собой функцию истинности или ложности простых. Эту функцию называют булевой функцией суждений f (a, b).

Порядок выполнения логических операций в сложном логическом выражении: n n n инверсия; конъюнкция; дизъюнкция; импликация; эквивалентность. Для изменения указанного порядка выполнения операций используются скобки.

Инверсия это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими простыми слова, данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО. А ¬А 1 0 0 1

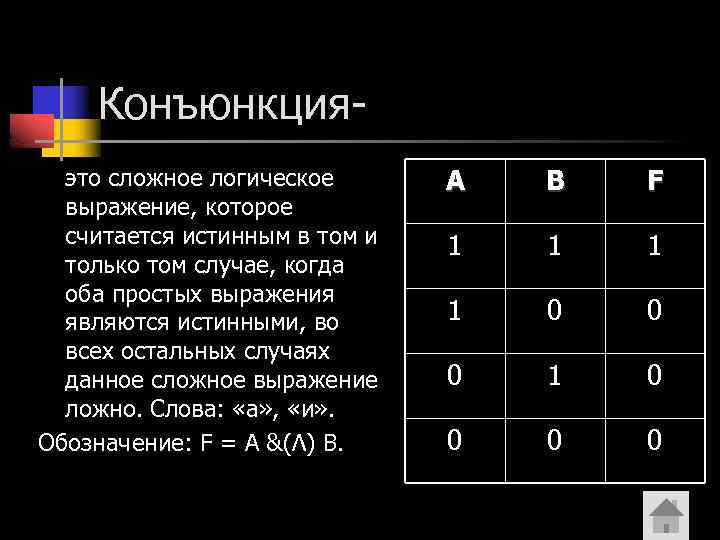Конъюнкцияэто сложное логическое выражение, которое считается истинным в том и только том случае, когда оба простых выражения являются истинными, во всех остальных случаях данное сложное выражение ложно. Слова: «а» , «и» . Обозначение: F = A &(Λ) B. A B F 1 1 0 0 0 1 0 0

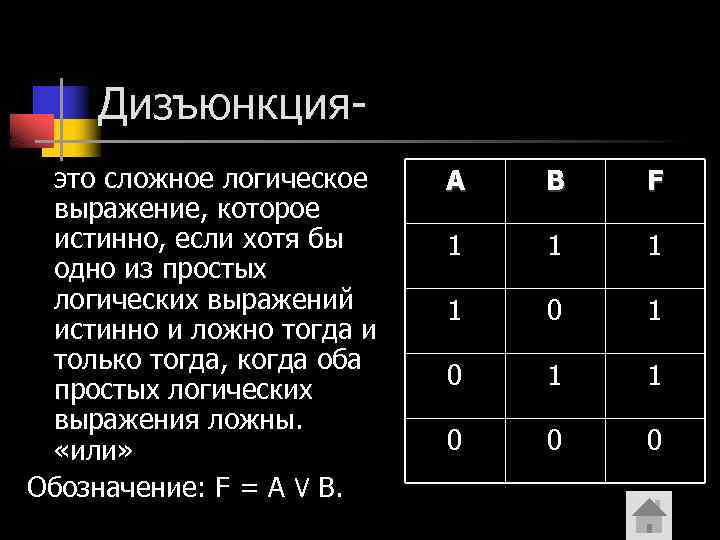Дизъюнкцияэто сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выражения ложны. «или» Обозначение: F = A ٧ B. A B F 1 1 0 0 0

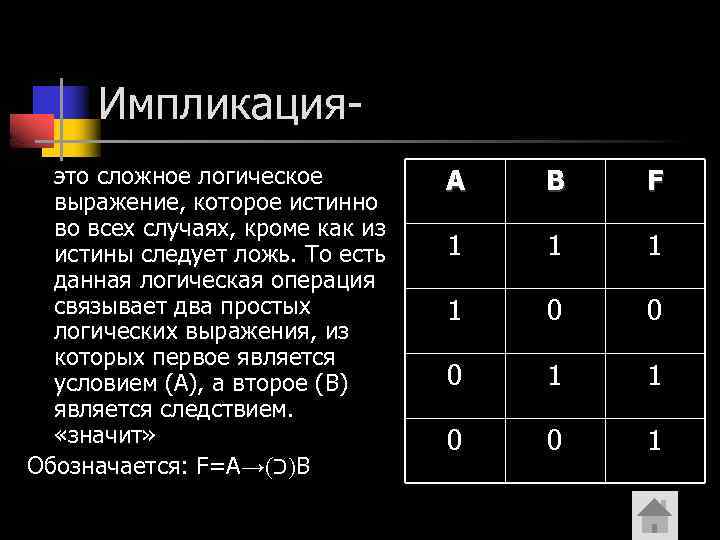Импликацияэто сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. То есть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А), а второе (В) является следствием. «значит» Обозначается: F=A→( )כ B A B F 1 1 0 0 0 1 1 0 0 1

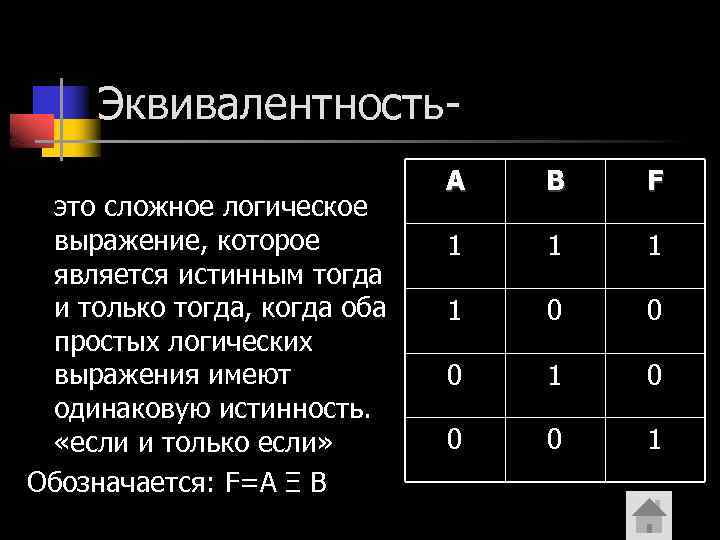Эквивалентностьэто сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность. «если и только если» Обозначается: F=A Ξ B A B F 1 1 0 0 0 1

Алгоритм построения таблиц истинности для сложных выражений: n Определить количество строк: количество строк = 2 n + строка для заголовка, n - количество простых высказываний. n Определить количество столбцов: количество столбцов = количество переменных + количество логических операций; определить количество переменных (простых выражений); логических операций и последовательность их выполнения. n Заполнить столбцы результатами выполнения логических операций в обозначенной последовательности с учетом таблиц истинности основных логических операций.

Пример 1: F=A٧(B ٧ ¬ B ―› ¬ C) Определяем количество строк: 3 2 =8+1=9 Определяем количество столбцов: 3+5=8 Строим таблицу:

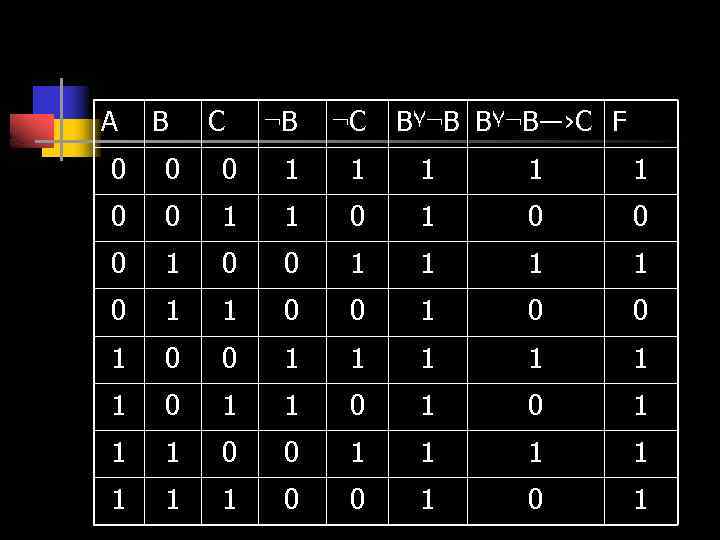A B C ¬B ¬C B٧¬B―›C F 0 0 0 1 1 1 0 0 0 1 1 1 1 0 0 1 1 1 0 1 1 1 0 0 1

Пример 2: Задача: Определить участника преступления, исходя из двух посылок: 1) "Если Иванов не участвовал или Петров участвовал, то Сидоров участвовал"; 2) "Если Иванов не участвовал, то Сидоров не участвовал".

Пример 2: Решение 1. Составим выражения: I - "Иванов участвовал в преступлении"; P - "Петров участвовал в преступлении"; S - "Сидоров участвовал в преступлении".

Пример 2: 2. Запишем условия в виде формул: ¬I ٧ P‹―S и ¬ I ―› ¬ S , тогда: F(I, P, S)=(¬ I ٧P‹―S)&(¬I―›¬S) 3. Найдем результат, используя таблицу истинности. Ответ: Иванов участвовал в преступлении.

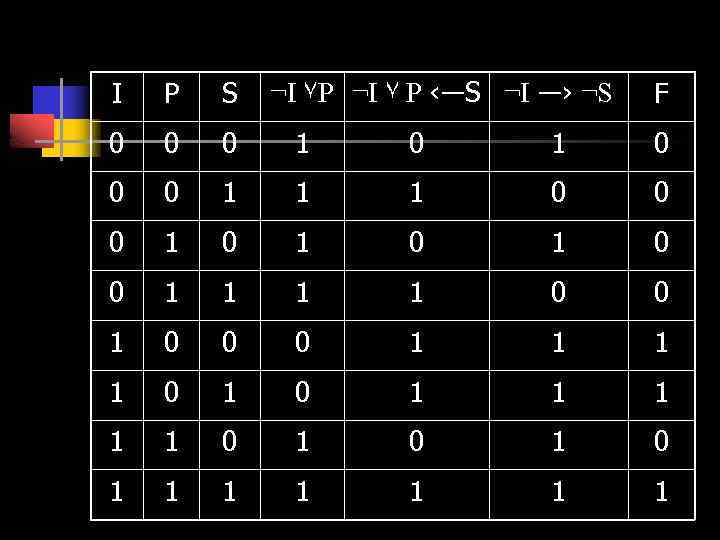¬I ٧P ¬I ٧ P ‹―S ¬I ―› ¬S I P S F 0 0 0 1 1 1 0 0 0 1 0 1 0 0 1 0 0 0 1 1 1 1 0 1 0 1 0 1 1 1 1

Спасибо за внимание!