Выполнила Фокина о 11 ж класс ВСОШ

Выполнила : Фокина о 11 ж класс ВСОШ№ 7 Руководитель: Бессонова Т. Д. г. Мурманск 2008

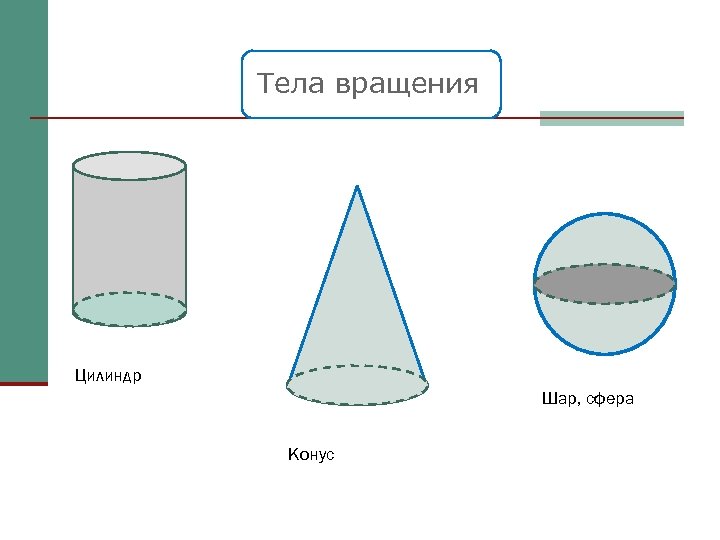Тела вращения Цилиндр Шар, сфера Конус

ГДЕ МОЖНО ВСТРЕТИТЬ ЦИЛИНДР?

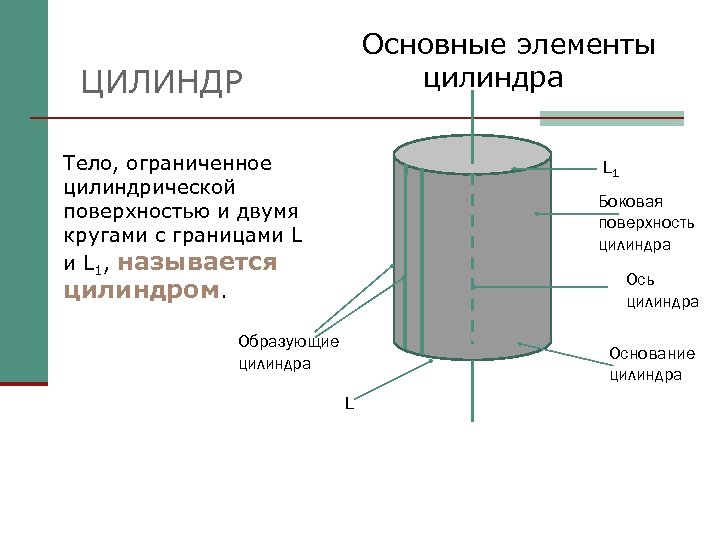Основные элементы цилиндра ЦИЛИНДР Тело, ограниченное цилиндрической поверхностью и двумя кругами с границами L 1, называется цилиндром. L 1 Боковая поверхность цилиндра Ось цилиндра Образующие цилиндра Основание цилиндра L

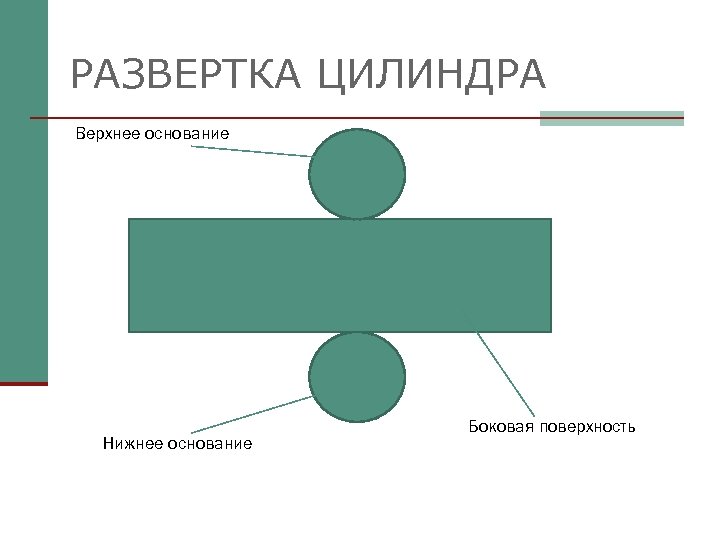РАЗВЕРТКА ЦИЛИНДРА Верхнее основание Нижнее основание Боковая поверхность

ПЛОЩАДЬ ПОВЕРХНОСТИ И ОБЪЕМ ЦИЛИНДРА За площадь боковой поверхности цилиндра принимается площадь ее развертки. Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований. Объем цилиндра равен произведению площади основания на высоту

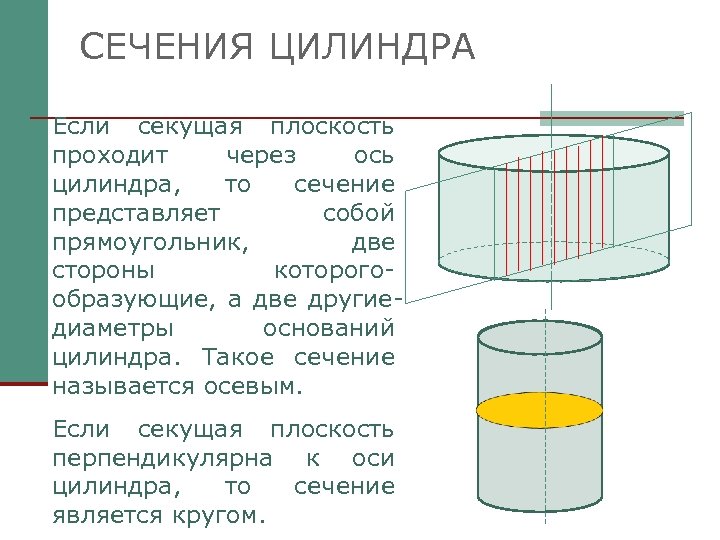СЕЧЕНИЯ ЦИЛИНДРА Если секущая плоскость проходит через ось цилиндра, то сечение представляет собой прямоугольник, две стороны которогообразующие, а две другиедиаметры оснований цилиндра. Такое сечение называется осевым. Если секущая плоскость перпендикулярна к оси цилиндра, то сечение является кругом.

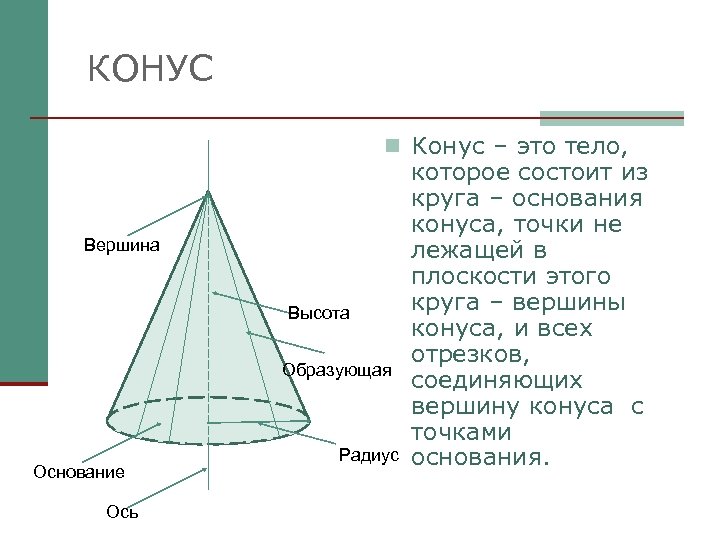КОНУС n Конус – это тело, Вершина Высота Образующая Основание Ось Радиус которое состоит из круга – основания конуса, точки не лежащей в плоскости этого круга – вершины конуса, и всех отрезков, соединяющих вершину конуса с точками основания.

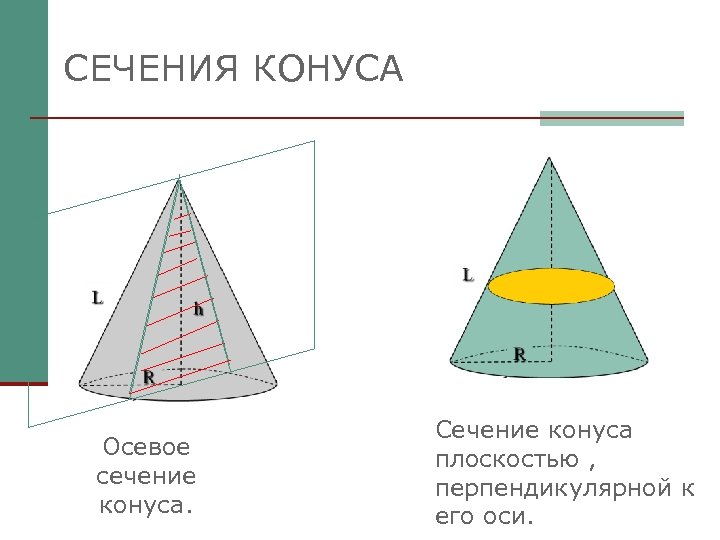СЕЧЕНИЯ КОНУСА Осевое сечение конуса. Сечение конуса плоскостью , перпендикулярной к его оси.

ПЛОЩАДЬ ПОВЕРХНОСТИ КОНУСА – площадь боковой поверхности конуса. – площадь полной поверхности конуса. L R – объём конуса.

ЗАДАЧА № 1 Высота конуса равна 8 см, а радиус основания равен 6 см. Найти площадь боковой поверхности конуса. Решение: S= π RL, по т. Пифагора. L² =r ² +h ² L ² =8 ²+6 ² L² =64+36 L² = 100 L =10 S= π R L S=π6*10 S=60 π(см) ²

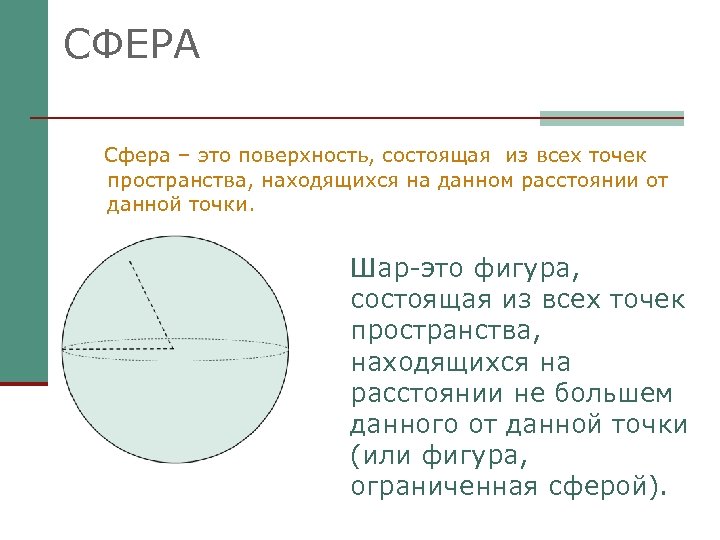СФЕРА Сфера – это поверхность, состоящая из всех точек пространства, находящихся на данном расстоянии от данной точки. Шар-это фигура, состоящая из всех точек пространства, находящихся на расстоянии не большем данного от данной точки (или фигура, ограниченная сферой).

ГДЕ МОЖНО ВСТРЕТИТЬ СФЕРУ?

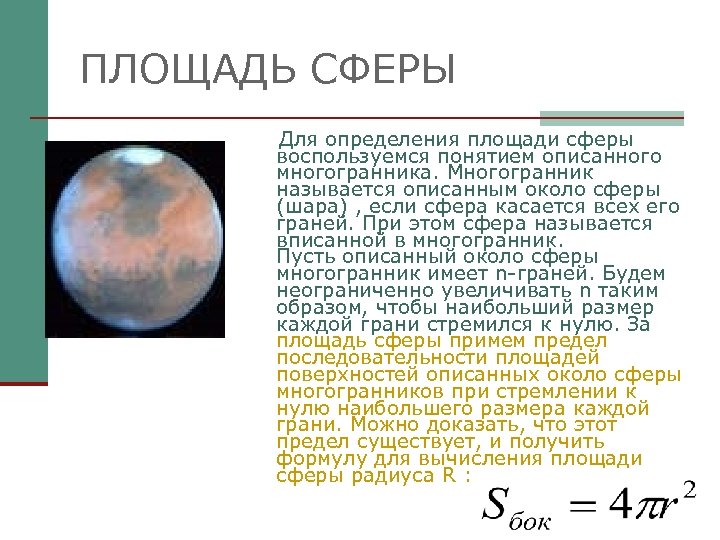ПЛОЩАДЬ СФЕРЫ Для определения площади сферы воспользуемся понятием описанного многогранника. Многогранник называется описанным около сферы (шара) , если сфера касается всех его граней. При этом сфера называется вписанной в многогранник. Пусть описанный около сферы многогранник имеет n-граней. Будем неограниченно увеличивать n таким образом, чтобы наибольший размер каждой грани стремился к нулю. За площадь сферы примем предел последовательности площадей поверхностей описанных около сферы многогранников при стремлении к нулю наибольшего размера каждой грани. Можно доказать, что этот предел существует, и получить формулу для вычисления площади сферы радиуса R :

ФОРМУЛЫ n - площадь боковой поверхности сферы. - объём шара.

ЗАДАЧА№ 1 Секущая плоскость проведена на расстоянии 6 см от центра шара. Радиус сечения равен 8 см. Найти объём шара. Решение V= 4/3πR³ Рассмотрим треугольник OO M o 1 По теореме Пифагора R²= d² + r² M R² = 36 +64 R² =100 o R = 10 V= 4/3π*103 V=4/31000 π V = 4000/3 π ≈1333π (cм) ³ 1 Ответ: 1333 π cм ³

УРАВНЕНИЕ СФЕРЫ n В прямоугольной системе координат уравнение сферы радиуса R с центром С (х0; у0; z 0) имеет вид (х-х0)2+(у-у0)2+(z-z 0)2=R 2

ШАРОВОЙ СЕГМЕНТ Шаровым сегментом называется часть шара, отсекаемая от него какой-нибудь плоскостью. Круг, получившийся в сечении, называется основанием каждого из этих сегментов. Объём шарового сегмента

ШАРОВОЙ СЕКТОР n Шаровым сектором называется тело, полученное вращением кругового сектора с углом, меньшим 900 , вокруг прямой, содержащей один из ограничивающих круговой сектор радиусов. n Формула нахождения объема шарового сектора

ЛИТЕРАТУРА 1. Л. С. Атанасян «Геометрия» 10 -11 класс «Просвещение» 2006 г 2. Рисунки из интернет сайт http: //www. alleng. ru/