Вычислительная математика Лекция 2 1 Тема 2

Вычислительная математика Лекция 2 1

Тема 2. Решение нелинейных алгебраических уравнений Постановка задачи: o Дано: нелинейное уравнение f(x) = 0 (1) o Найти: корень (решение) – числовое значение ξ, при подстановке которого в (1) уравнение обращается в верное равенство. 2

5. Метод простой итерации Необходимо преобразовать уравнение f(x) = 0 к виду x = φ(x) так, чтобы φ(x) непрерывно дифференцируема на [a, b] и f(ξ) = 0 ξ = φ(ξ). Далее, пусть x 0 [a, b]. Строится последовательность x 1, x 2, …, xk , …, где xk = φ(xk-1), k = 1, 2, …. 3

5. Метод простой итерации Теорема (достаточное условие сходимости) Если выполнено условие |φ (x)| q < 1 при x [a, b], то и справедливы оценки: 4

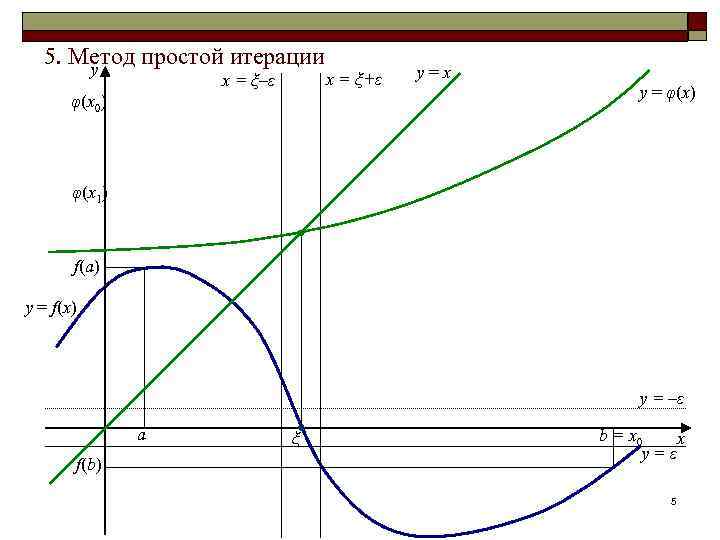5. Метод простой итерации y x = ξ–ε φ(x 0) x = ξ+ε y=x y = φ(x) φ(x 1) f(a) y = f(x) y = –ε a f(b) ξ b = x 0 x y=ε 5

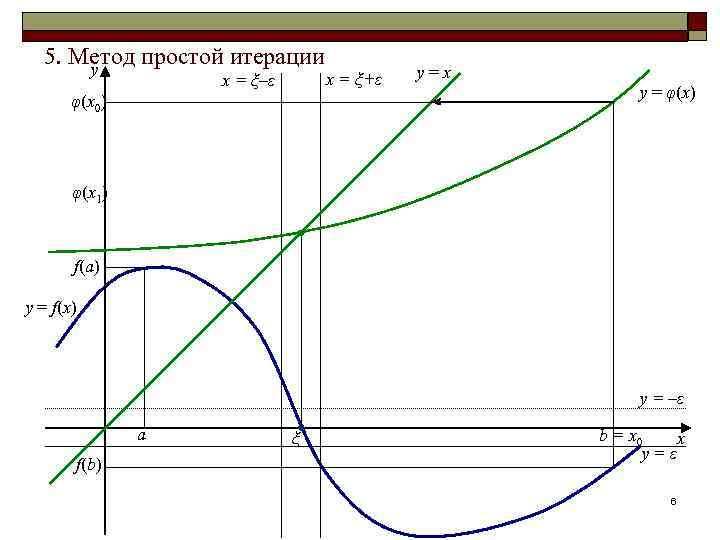5. Метод простой итерации y x = ξ–ε φ(x 0) x = ξ+ε y=x y = φ(x) φ(x 1) f(a) y = f(x) y = –ε a f(b) ξ b = x 0 x y=ε 6

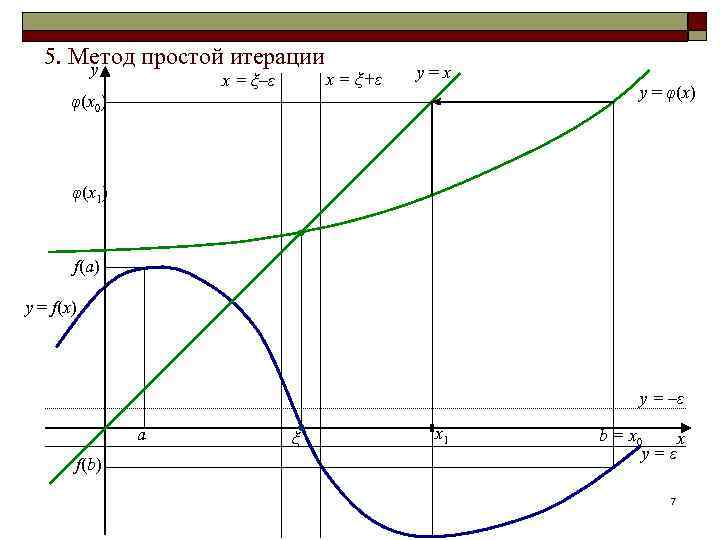5. Метод простой итерации y x = ξ–ε x = ξ+ε y=x φ(x 0) y = φ(x) φ(x 1) f(a) y = f(x) y = –ε a f(b) ξ x 1 b = x 0 x y=ε 7

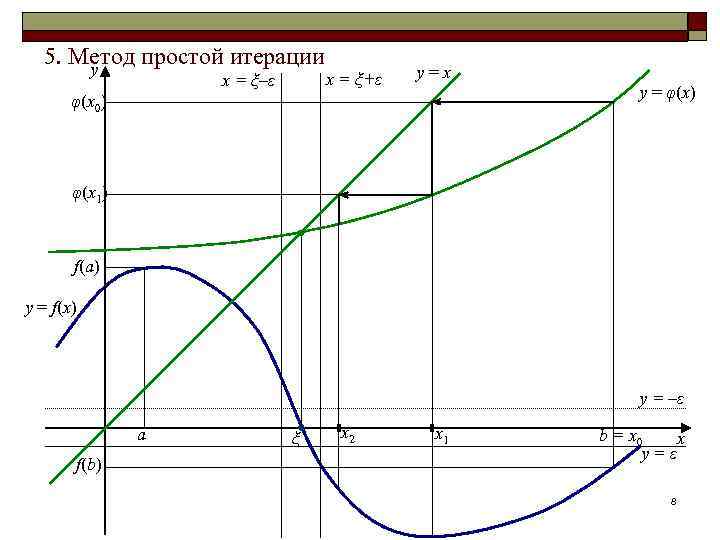5. Метод простой итерации y x = ξ–ε x = ξ+ε y=x φ(x 0) y = φ(x) φ(x 1) f(a) y = f(x) y = –ε a f(b) ξ x 2 x 1 b = x 0 x y=ε 8

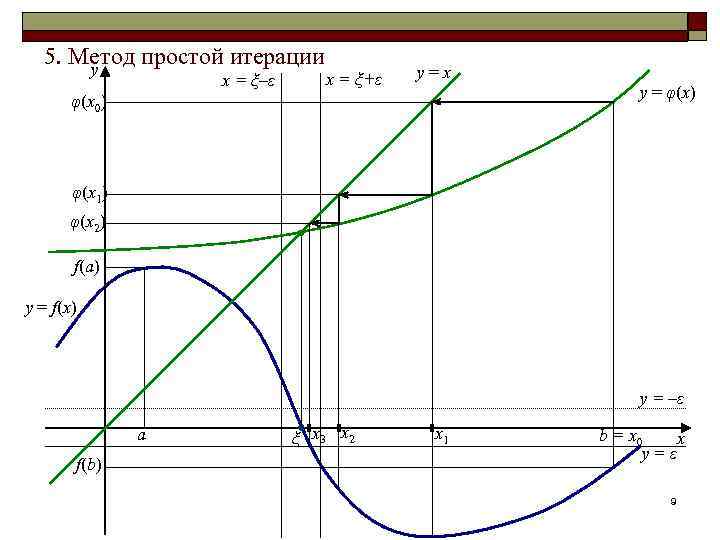5. Метод простой итерации y x = ξ–ε x = ξ+ε y=x φ(x 0) y = φ(x) φ(x 1) φ(x 2) f(a) y = f(x) y = –ε a f(b) ξ x 3 x 2 x 1 b = x 0 x y=ε 9

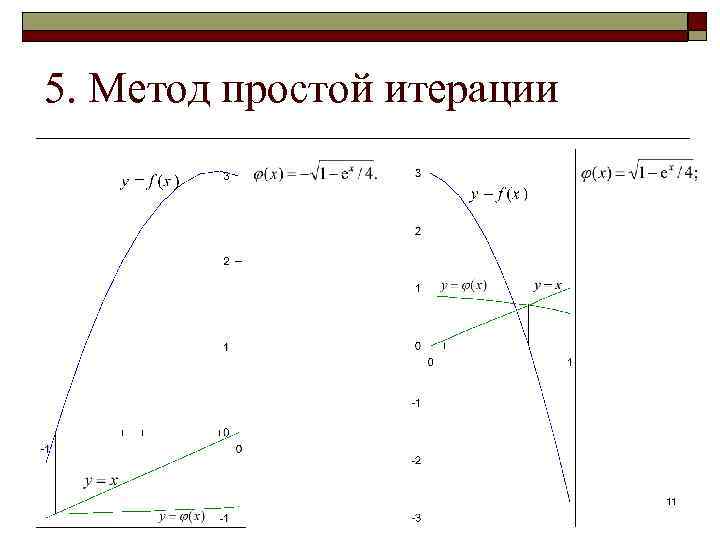
5. Метод простой итерации Пример преобразования: - для нахождения положительного корня: - для нахождения отрицательного корня: 10

5. Метод простой итерации 11

5. Метод простой итерации Общее описание метода: Шаг 1. x 0 = a (x 0 = b), k = 0; Шаг 2. Шаг 3. Если |xk+1 – xk| < ε или (и) |f(xk+1)| < ε, то ξ ≈ xk+1, иначе k = k +1 и Шаг 2. 12

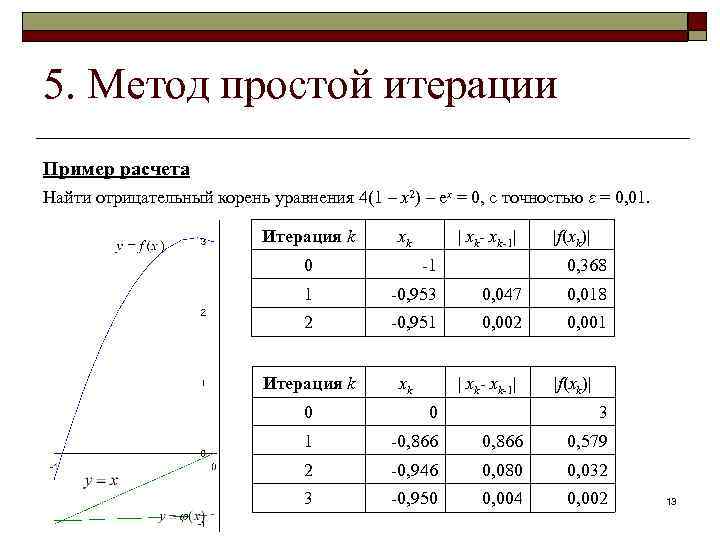5. Метод простой итерации Пример расчета Найти отрицательный корень уравнения 4(1 – x 2) – ex = 0, с точностью ε = 0, 01. Итерация k xk | xk-1| |f(xk)| 0 -1 1 -0, 953 0, 047 0, 018 2 -0, 951 0, 002 0, 001 Итерация k xk 0, 368 | xk-1| |f(xk)| 0 0 3 1 -0, 866 0, 579 2 -0, 946 0, 080 0, 032 3 -0, 950 0, 004 0, 002 13

5. Метод простой итерации Пример расчета Найти положительный корень уравнения 4(1 – x 2) – ex = 0, с точностью ε = 0, 01. Итерация k xk | xk-1| |f(xk)| 0 0 3 1 0, 866 1, 377 2 0, 637 0, 229 0, 487 3 0, 726 0, 089 0, 177 4 0, 6951 0, 031 0, 063 5 0, 7064 0, 011 0, 023 6 0, 7024 0, 008 14

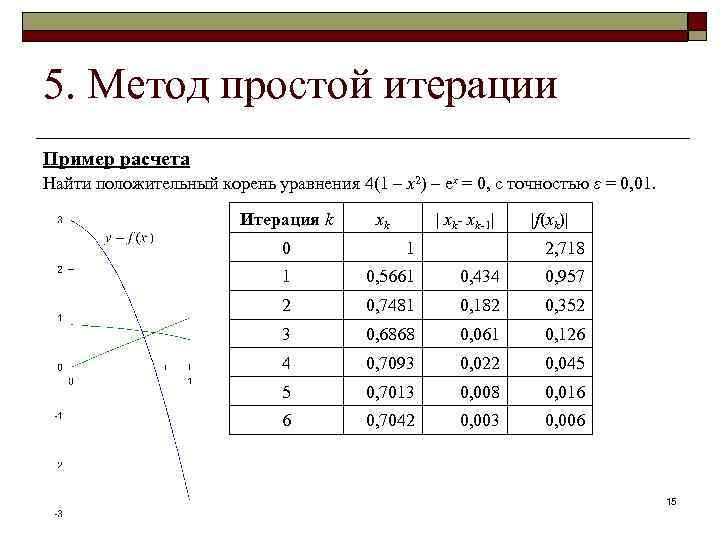5. Метод простой итерации Пример расчета Найти положительный корень уравнения 4(1 – x 2) – ex = 0, с точностью ε = 0, 01. Итерация k xk | xk-1| |f(xk)| 0 1 2, 718 1 0, 5661 0, 434 0, 957 2 0, 7481 0, 182 0, 352 3 0, 6868 0, 061 0, 126 4 0, 7093 0, 022 0, 045 5 0, 7013 0, 008 0, 016 6 0, 7042 0, 003 0, 006 15

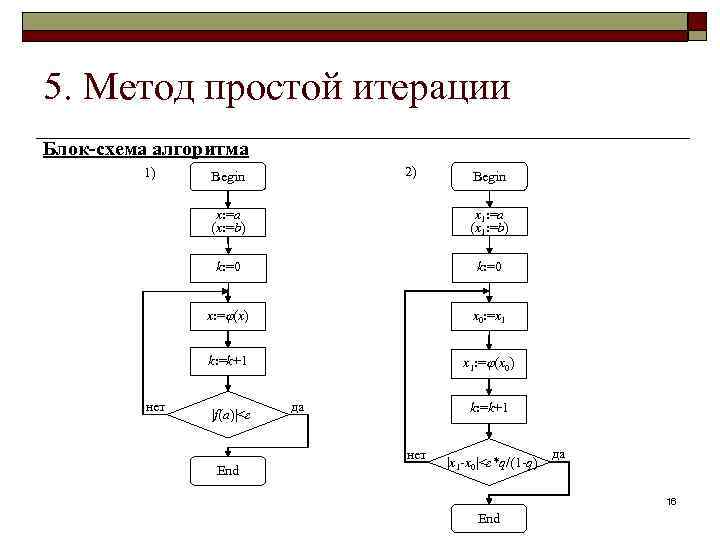5. Метод простой итерации Блок-схема алгоритма 1) 2) Begin x: =a (x: =b) k: =0 x: = (x) x 0: =x 1 k: =k+1 нет x 1: =a (x 1: =b) x 1: = (x 0) |f(a)|<ε да k: =k+1 нет End |x 1 -x 0|<ε*q/(1 -q) да 16 End

Ввод исходных данных в программу на языке Pascal const eps = 0. 001; var a, b: double; function f(x: double): double; begin f : = 4*(1 – sqr(x)) – exp(x); end; function df(x: double): double; { f (x) } begin df : = 8*(x) – exp(x); end; function fi(x: double): double; { φ(x) } begin fi : = sqrt(1 – exp(x)/4); end; begin a : = 0; b : = 1; . . . end. 17