Выч. матем 2012 СЛАУ.ppt
- Количество слайдов: 55
 Вычислительная математика Лекция 1 1
Вычислительная математика Лекция 1 1
 Задачи курса o Изучение вычислительных (численных) методов – методов решения математических задач с помощью ЭВМ. o Программная реализация вычислительных методов и анализ результатов. o Решение математических задач вычислительными методами с помощью пакетов прикладных программ. 2
Задачи курса o Изучение вычислительных (численных) методов – методов решения математических задач с помощью ЭВМ. o Программная реализация вычислительных методов и анализ результатов. o Решение математических задач вычислительными методами с помощью пакетов прикладных программ. 2
 Изучение численных методов o Рассматриваются вычислительные методы решения корректных задач (имеющих единственное решение, устойчивое к погрешностям входных данных). o Рассматриваются алгоритмы и оценки погрешности вычислительных методов 3
Изучение численных методов o Рассматриваются вычислительные методы решения корректных задач (имеющих единственное решение, устойчивое к погрешностям входных данных). o Рассматриваются алгоритмы и оценки погрешности вычислительных методов 3
 Темы занятий o o Алгебра 1. Решение систем линейных алгебраических уравнений (СЛАУ). 2. Решение нелинейных алгебраических уравнений. Математический анализ 3. Приближение функций. 4. Вычисление определенных интегралов. 5. Решение дифференциальных уравнений. 4
Темы занятий o o Алгебра 1. Решение систем линейных алгебраических уравнений (СЛАУ). 2. Решение нелинейных алгебраических уравнений. Математический анализ 3. Приближение функций. 4. Вычисление определенных интегралов. 5. Решение дифференциальных уравнений. 4
 Тема 1. Решение систем линейных алгебраических уравнений (СЛАУ) Постановка задачи: o Дано: система линейных алгебраических уравнений в матричной форме записи: o Найти: вектор неизвестных x = (x 1, x 2, …, xn)T (xj R), при подстановке которого в СЛАУ все уравнения обращаются в верное равенство 5
Тема 1. Решение систем линейных алгебраических уравнений (СЛАУ) Постановка задачи: o Дано: система линейных алгебраических уравнений в матричной форме записи: o Найти: вектор неизвестных x = (x 1, x 2, …, xn)T (xj R), при подстановке которого в СЛАУ все уравнения обращаются в верное равенство 5
 Методы решения СЛАУ o o Точные методы: - формулы Крамера; - метод матричного исчисления (нахождение обратной матрицы); - метод Гаусса (исключения неизвестных); … Приближенные (итерационные методы): - метод простой итерации; - метод Зейделя; … 6
Методы решения СЛАУ o o Точные методы: - формулы Крамера; - метод матричного исчисления (нахождение обратной матрицы); - метод Гаусса (исключения неизвестных); … Приближенные (итерационные методы): - метод простой итерации; - метод Зейделя; … 6
 Метод Гаусса o Прямой ход: последовательное исключение неизвестных: x 1 из уравнений 2, 3, …, n; x 2 из уравнений 3, 4, …, n; … xk из уравнений k+1, k+2, …, n; … xn-1 из уравнения n; o Обратный ход: последовательное вычисление значений неизвестных xn, xn-1, …, x 1. 7
Метод Гаусса o Прямой ход: последовательное исключение неизвестных: x 1 из уравнений 2, 3, …, n; x 2 из уравнений 3, 4, …, n; … xk из уравнений k+1, k+2, …, n; … xn-1 из уравнения n; o Обратный ход: последовательное вычисление значений неизвестных xn, xn-1, …, x 1. 7
 Алгоритм метода Гаусса для n = 4 Прямой ход Шаг 1. Пусть. С помощью элементарных преобразований x 1 исключается из уравнений 2, 3, 4 (зануляются элементы первого столбца, стоящие ниже главной диагонали). Получим расширенную матрицу где 8
Алгоритм метода Гаусса для n = 4 Прямой ход Шаг 1. Пусть. С помощью элементарных преобразований x 1 исключается из уравнений 2, 3, 4 (зануляются элементы первого столбца, стоящие ниже главной диагонали). Получим расширенную матрицу где 8
 Алгоритм метода Гаусса для n = 4 Прямой ход Шаг 2. Пусть. С помощью элементарных преобразований x 1 исключается из уравнений 3, 4 (зануляются элементы второго столбца, стоящие ниже главной диагонали). Получим расширенную матрицу где 9
Алгоритм метода Гаусса для n = 4 Прямой ход Шаг 2. Пусть. С помощью элементарных преобразований x 1 исключается из уравнений 3, 4 (зануляются элементы второго столбца, стоящие ниже главной диагонали). Получим расширенную матрицу где 9
 Алгоритм метода Гаусса для n = 4 Прямой ход Шаг 3. Пусть. С помощью элементарных преобразований x 1 исключается из уравнения 4 (зануляется элемент третьего столбца, стоящий ниже главной диагонали). Получим расширенную матрицу где 10
Алгоритм метода Гаусса для n = 4 Прямой ход Шаг 3. Пусть. С помощью элементарных преобразований x 1 исключается из уравнения 4 (зануляется элемент третьего столбца, стоящий ниже главной диагонали). Получим расширенную матрицу где 10
 Алгоритм метода Гаусса для n = 4 После преобразований СЛАУ имеет следующий вид: 11
Алгоритм метода Гаусса для n = 4 После преобразований СЛАУ имеет следующий вид: 11
 Алгоритм метода Гаусса для n = 4 Обратный ход: вычисляются значения неизвестных 12
Алгоритм метода Гаусса для n = 4 Обратный ход: вычисляются значения неизвестных 12
 Пример решения СЛАУ методом Гаусса для n = 4 Прямой ход: преобразования расширенной матрицы 13
Пример решения СЛАУ методом Гаусса для n = 4 Прямой ход: преобразования расширенной матрицы 13
 Пример решения СЛАУ методом Гаусса для n = 4 Обратный ход: 14
Пример решения СЛАУ методом Гаусса для n = 4 Обратный ход: 14
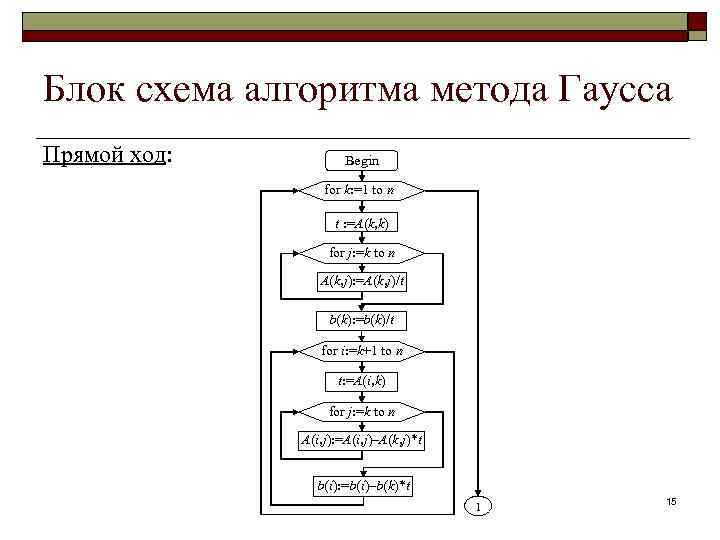 Блок схема алгоритма метода Гаусса Прямой ход: Begin for k: =1 to n t : =A(k, k) for j: =k to n A(k, j): =A(k, j)/t b(k): =b(k)/t for i: =k+1 to n t: =A(i, k) for j: =k to n A(i, j): =A(i, j)–A(k, j)*t b(i): =b(i)–b(k)*t 1 15
Блок схема алгоритма метода Гаусса Прямой ход: Begin for k: =1 to n t : =A(k, k) for j: =k to n A(k, j): =A(k, j)/t b(k): =b(k)/t for i: =k+1 to n t: =A(i, k) for j: =k to n A(i, j): =A(i, j)–A(k, j)*t b(i): =b(i)–b(k)*t 1 15
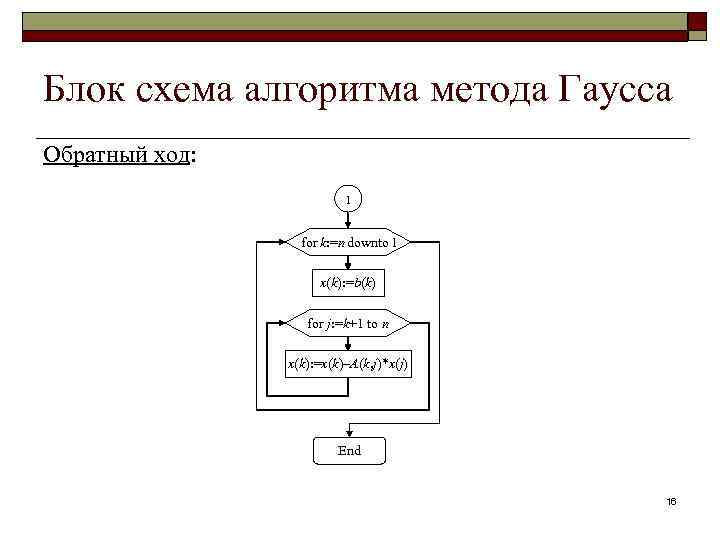 Блок схема алгоритма метода Гаусса Обратный ход: 1 for k: =n downto 1 x(k): =b(k) for j: =k+1 to n x(k): =x(k)–A(k, j)*x(j) End 16
Блок схема алгоритма метода Гаусса Обратный ход: 1 for k: =n downto 1 x(k): =b(k) for j: =k+1 to n x(k): =x(k)–A(k, j)*x(j) End 16
 Ввод исходных данных в программу и вывод на экран на языке Pascal const n = 4; {размерность системы} var A: array[1. . n, 1. . n] of double = (( 1, 1, 2, 3), {матрица системы (двумерный массив)} ( 1, 2, 3, -1), ( 3, -1, -2), ( 2, 3, -1)); b: array[1. . n] of double = (1, -4, -6); {правая часть системы (одномерный массив)} i, j: integer; {вспомогательные переменные} begin {вывод данных на консольный экран} for i: =1 to n do begin for j: =1 to n do write(A[i, j]: 6: 0); writeln(b[i]: 6: 0); end; readln; end. 17
Ввод исходных данных в программу и вывод на экран на языке Pascal const n = 4; {размерность системы} var A: array[1. . n, 1. . n] of double = (( 1, 1, 2, 3), {матрица системы (двумерный массив)} ( 1, 2, 3, -1), ( 3, -1, -2), ( 2, 3, -1)); b: array[1. . n] of double = (1, -4, -6); {правая часть системы (одномерный массив)} i, j: integer; {вспомогательные переменные} begin {вывод данных на консольный экран} for i: =1 to n do begin for j: =1 to n do write(A[i, j]: 6: 0); writeln(b[i]: 6: 0); end; readln; end. 17
 Ввод исходных данных в программу и вывод на экран на языке Pascal const {максимальный размер матрицы системы} nmax = 10; var data: text; {ссылка на файл с исходными данными} n: integer; {размерность системы} {матрица системы (двумерный массив)} A: array[1. . nmax, 1. . nmax] of double; b: array[1. . nmax] of double; {правая часть системы} i, j: integer; {вспомогательные переменные} begin {установить связь с файлом на диске} Assign. File(data, 'system. txt'); Reset(data); {открыть файл для чтения} {считать из файла размерность системы} readln(data, n); {ввод данных из файла} for i: =1 to n do begin for j: =1 to n do read(data, A[i, j]); readln(data, b[i]); end; {вывод данных на экран} for i: =1 to n do begin for j: =1 to n do write(A[i, j]: 6: 0); writeln(b[i]: 6: 0); end; readln; 18 end.
Ввод исходных данных в программу и вывод на экран на языке Pascal const {максимальный размер матрицы системы} nmax = 10; var data: text; {ссылка на файл с исходными данными} n: integer; {размерность системы} {матрица системы (двумерный массив)} A: array[1. . nmax, 1. . nmax] of double; b: array[1. . nmax] of double; {правая часть системы} i, j: integer; {вспомогательные переменные} begin {установить связь с файлом на диске} Assign. File(data, 'system. txt'); Reset(data); {открыть файл для чтения} {считать из файла размерность системы} readln(data, n); {ввод данных из файла} for i: =1 to n do begin for j: =1 to n do read(data, A[i, j]); readln(data, b[i]); end; {вывод данных на экран} for i: =1 to n do begin for j: =1 to n do write(A[i, j]: 6: 0); writeln(b[i]: 6: 0); end; readln; 18 end.
 Выполнение проверки for i: =1 to n do begin sum: =0; {sum – переменная типа double} for j: =1 to n do sum: =sum+A[i, j]*x[j]; razn: =abs(sum–b[i]); {razn – переменная типа double} writeln(sum: 10: 6, ' (', razn: 7: 6, ')'); end; 19
Выполнение проверки for i: =1 to n do begin sum: =0; {sum – переменная типа double} for j: =1 to n do sum: =sum+A[i, j]*x[j]; razn: =abs(sum–b[i]); {razn – переменная типа double} writeln(sum: 10: 6, ' (', razn: 7: 6, ')'); end; 19
 Приближенные (итерационные) методы решения СЛАУ Обозначим решение СЛАУ Последовательность векторов сходится к вектору , если Итерационные методы решения СЛАУ – методы последовательных приближений: строится последовательность векторов до тех пор, пока не выполнится условие: , где δ – заданное число 20
Приближенные (итерационные) методы решения СЛАУ Обозначим решение СЛАУ Последовательность векторов сходится к вектору , если Итерационные методы решения СЛАУ – методы последовательных приближений: строится последовательность векторов до тех пор, пока не выполнится условие: , где δ – заданное число 20
 Метод простой итерации (Якоби) СЛАУ Ax = c преобразуется к виду x = Bx + d: 21
Метод простой итерации (Якоби) СЛАУ Ax = c преобразуется к виду x = Bx + d: 21
 Метод простой итерации (Якоби) В векторной форме: x = Bx + d; 22
Метод простой итерации (Якоби) В векторной форме: x = Bx + d; 22
 Метод простой итерации (Якоби) Алгоритм решения СЛАУ Строим последовательность векторов : … … 23
Метод простой итерации (Якоби) Алгоритм решения СЛАУ Строим последовательность векторов : … … 23
 Метод простой итерации (Якоби) В векторной форме: x(0) = d; x(1) = Bx(0) + d; x(2) = Bx(1) + d; … x(k) = Bx(k–l) + d; … 24
Метод простой итерации (Якоби) В векторной форме: x(0) = d; x(1) = Bx(0) + d; x(2) = Bx(1) + d; … x(k) = Bx(k–l) + d; … 24
 Метод простой итерации (Якоби) Теорема (достаточное условие сходимости) Если выполнено условие то для любого x(0) и справедливы оценки погрешности: 25
Метод простой итерации (Якоби) Теорема (достаточное условие сходимости) Если выполнено условие то для любого x(0) и справедливы оценки погрешности: 25
 Метод простой итерации (Якоби) Критерий остановки вычислительного процесса: где ε – заданная точность. 26
Метод простой итерации (Якоби) Критерий остановки вычислительного процесса: где ε – заданная точность. 26
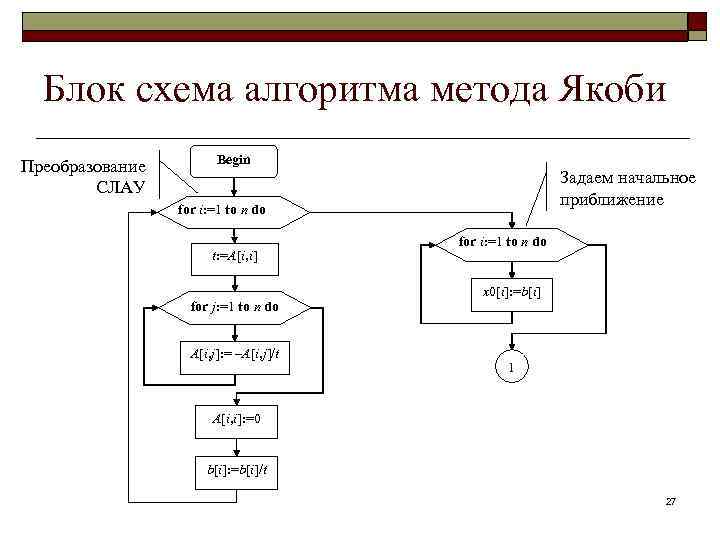 Блок схема алгоритма метода Якоби Преобразование СЛАУ Begin Задаем начальное приближение for i: =1 to n do t: =A[i, i] for j: =1 to n do A[i, j]: = –A[i, j]/t for i: =1 to n do x 0[i]: =b[i] 1 A[i, i]: =0 b[i]: =b[i]/t 27
Блок схема алгоритма метода Якоби Преобразование СЛАУ Begin Задаем начальное приближение for i: =1 to n do t: =A[i, i] for j: =1 to n do A[i, j]: = –A[i, j]/t for i: =1 to n do x 0[i]: =b[i] 1 A[i, i]: =0 b[i]: =b[i]/t 27
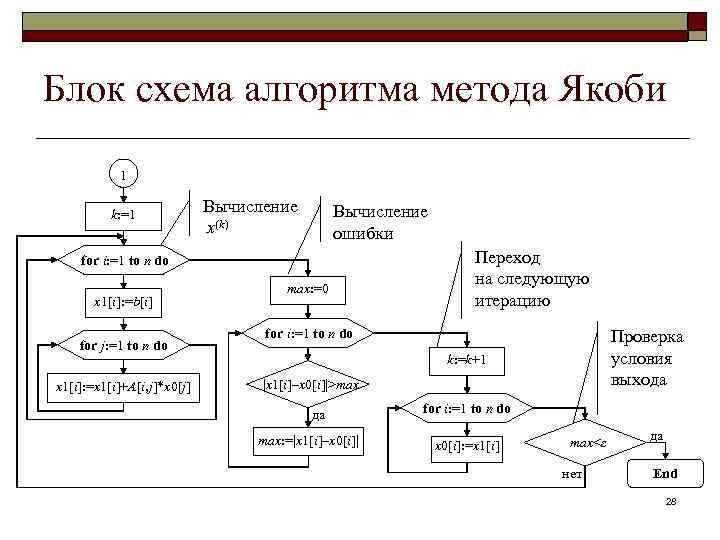 Блок схема алгоритма метода Якоби 1 k: =1 Вычисление x(k) Вычисление ошибки for i: =1 to n do x 1[i]: =b[i] for j: =1 to n do x 1[i]: =x 1[i]+A[i, j]*x 0[j] max: =0 Переход на следующую итерацию for i: =1 to n do Проверка условия выхода k: =k+1 |x 1[i]–x 0[i]|>max да max: =|x 1[i]–x 0[i]| for i: =1 to n do x 0[i]: =x 1[i] max<ε нет да End 28
Блок схема алгоритма метода Якоби 1 k: =1 Вычисление x(k) Вычисление ошибки for i: =1 to n do x 1[i]: =b[i] for j: =1 to n do x 1[i]: =x 1[i]+A[i, j]*x 0[j] max: =0 Переход на следующую итерацию for i: =1 to n do Проверка условия выхода k: =k+1 |x 1[i]–x 0[i]|>max да max: =|x 1[i]–x 0[i]| for i: =1 to n do x 0[i]: =x 1[i] max<ε нет да End 28
 Пример решения СЛАУ методом Якоби Решить СЛАУ методом Якоби с точностью ε = 0, 05. 29
Пример решения СЛАУ методом Якоби Решить СЛАУ методом Якоби с точностью ε = 0, 05. 29
 Пример решения СЛАУ методом Якоби Преобразуем СЛАУ: условие сходимости выполнено; 30
Пример решения СЛАУ методом Якоби Преобразуем СЛАУ: условие сходимости выполнено; 30
 Пример решения СЛАУ методом Якоби Выбираем начальное приближение: Итерация 1: 31
Пример решения СЛАУ методом Якоби Выбираем начальное приближение: Итерация 1: 31
 Пример решения СЛАУ методом Якоби Итерация 2: Итерация 3: 32
Пример решения СЛАУ методом Якоби Итерация 2: Итерация 3: 32
 Метод Зейделя Алгоритм решения СЛАУ Строим последовательность векторов : … … 33
Метод Зейделя Алгоритм решения СЛАУ Строим последовательность векторов : … … 33
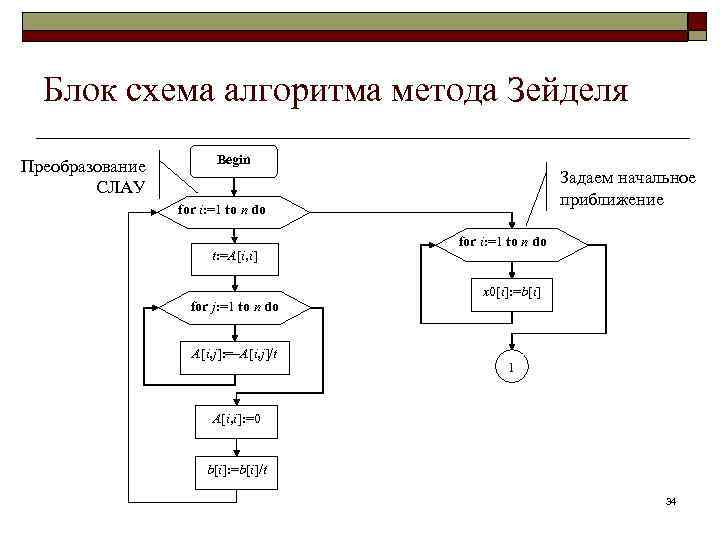 Блок схема алгоритма метода Зейделя Преобразование СЛАУ Begin Задаем начальное приближение for i: =1 to n do t: =A[i, i] for j: =1 to n do A[i, j]: =–A[i, j]/t for i: =1 to n do x 0[i]: =b[i] 1 A[i, i]: =0 b[i]: =b[i]/t 34
Блок схема алгоритма метода Зейделя Преобразование СЛАУ Begin Задаем начальное приближение for i: =1 to n do t: =A[i, i] for j: =1 to n do A[i, j]: =–A[i, j]/t for i: =1 to n do x 0[i]: =b[i] 1 A[i, i]: =0 b[i]: =b[i]/t 34
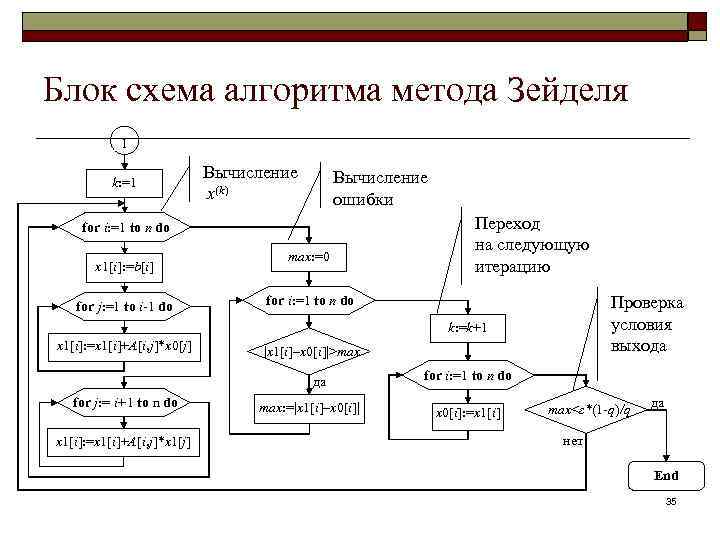 Блок схема алгоритма метода Зейделя 1 k: =1 Вычисление x(k) Вычисление ошибки for i: =1 to n do x 1[i]: =b[i] for j: =1 to i-1 do max: =0 Переход на следующую итерацию Проверка условия выхода for i: =1 to n do k: =k+1 x 1[i]: =x 1[i]+A[i, j]*x 0[j] |x 1[i]–x 0[i]|>max да for j: = i+1 to n do x 1[i]: =x 1[i]+A[i, j]*x 1[j] max: =|x 1[i]–x 0[i]| for i: =1 to n do x 0[i]: =x 1[i] max<ε*(1 -q)/q да нет End 35
Блок схема алгоритма метода Зейделя 1 k: =1 Вычисление x(k) Вычисление ошибки for i: =1 to n do x 1[i]: =b[i] for j: =1 to i-1 do max: =0 Переход на следующую итерацию Проверка условия выхода for i: =1 to n do k: =k+1 x 1[i]: =x 1[i]+A[i, j]*x 0[j] |x 1[i]–x 0[i]|>max да for j: = i+1 to n do x 1[i]: =x 1[i]+A[i, j]*x 1[j] max: =|x 1[i]–x 0[i]| for i: =1 to n do x 0[i]: =x 1[i] max<ε*(1 -q)/q да нет End 35
 Пример решения СЛАУ методом Зейделя Решить СЛАУ методом Зейделя с точностью ε = 0, 05. 36
Пример решения СЛАУ методом Зейделя Решить СЛАУ методом Зейделя с точностью ε = 0, 05. 36
 Пример решения СЛАУ методом Зейделя Преобразуем СЛАУ: условие сходимости выполнено; 37
Пример решения СЛАУ методом Зейделя Преобразуем СЛАУ: условие сходимости выполнено; 37
 Пример решения СЛАУ методом Зейделя Выбираем начальное приближение: Итерация 1: 38
Пример решения СЛАУ методом Зейделя Выбираем начальное приближение: Итерация 1: 38
 Пример решения СЛАУ методом Зейделя Итерация 2: Итерация 3: 39
Пример решения СЛАУ методом Зейделя Итерация 2: Итерация 3: 39
 Ввод исходных данных в программу и вывод на экран на языке Pascal const n = 4; {размерность системы} A: array[1. . n, 1. . n] of double = (( 1, 1, 2, 3), {матрица системы (двумерный массив)} ( 1, 2, 3, -1), ( 3, -1, -2), ( 2, 3, -1)); b: array[1. . n] of double = (1, -4, -6); {правая часть системы (одномерный массив)} var i, j: integer; {вспомогательные переменные} begin {вывод данных на консольный экран} for i: =1 to n do begin for j: =1 to n do write(A[i, j]: 6: 0); writeln(b[i]: 6: 0); end; readln; end. 40
Ввод исходных данных в программу и вывод на экран на языке Pascal const n = 4; {размерность системы} A: array[1. . n, 1. . n] of double = (( 1, 1, 2, 3), {матрица системы (двумерный массив)} ( 1, 2, 3, -1), ( 3, -1, -2), ( 2, 3, -1)); b: array[1. . n] of double = (1, -4, -6); {правая часть системы (одномерный массив)} var i, j: integer; {вспомогательные переменные} begin {вывод данных на консольный экран} for i: =1 to n do begin for j: =1 to n do write(A[i, j]: 6: 0); writeln(b[i]: 6: 0); end; readln; end. 40
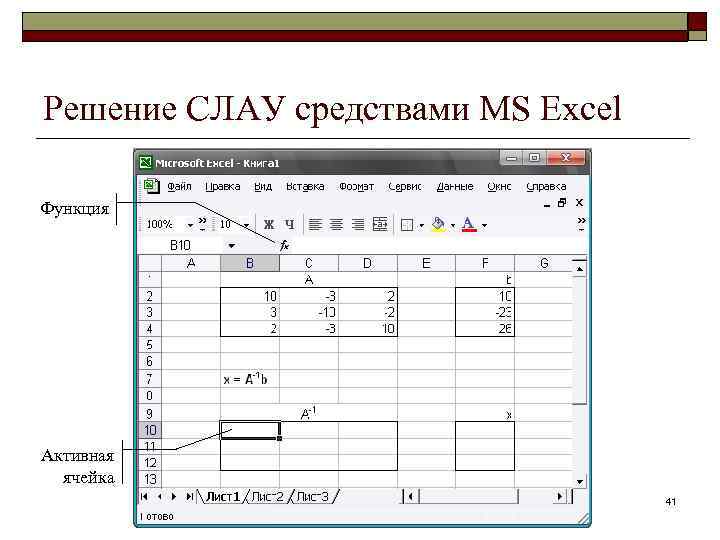 Решение СЛАУ средствами MS Excel Функция Активная ячейка 41
Решение СЛАУ средствами MS Excel Функция Активная ячейка 41
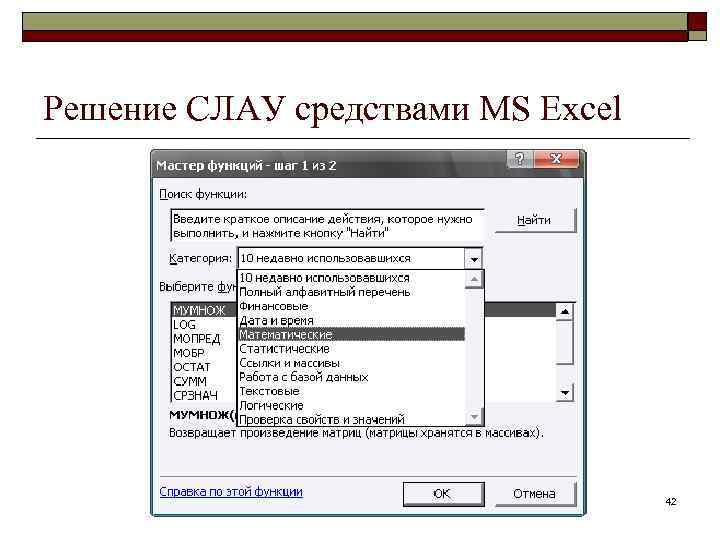 Решение СЛАУ средствами MS Excel 42
Решение СЛАУ средствами MS Excel 42
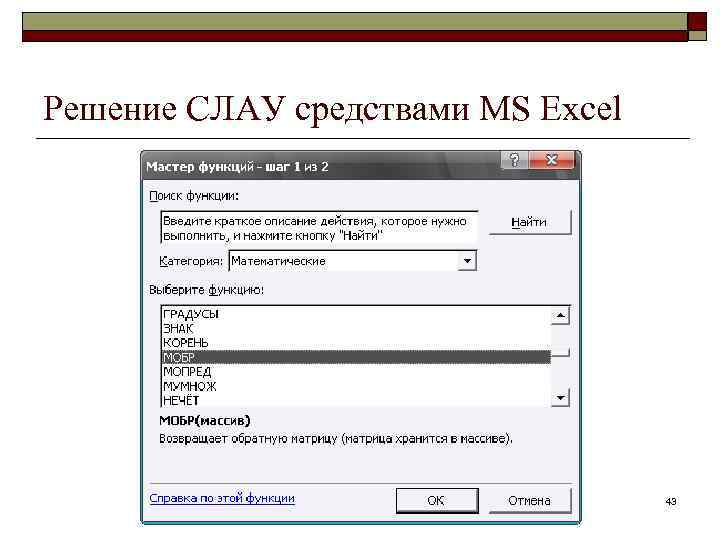 Решение СЛАУ средствами MS Excel 43
Решение СЛАУ средствами MS Excel 43
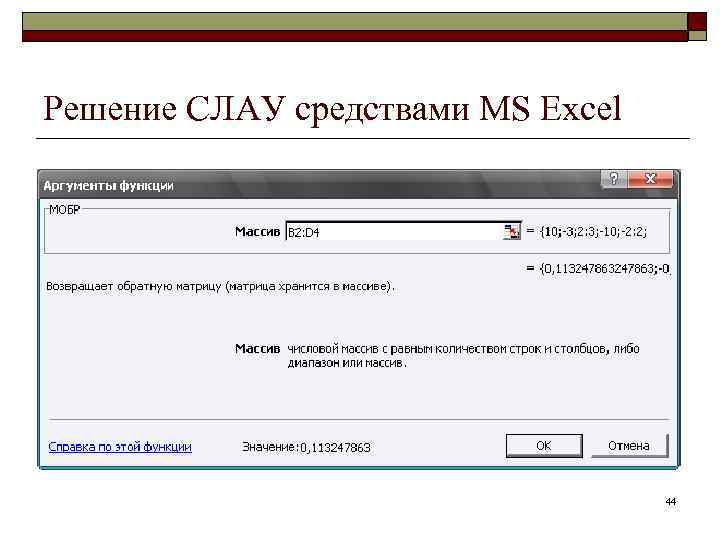 Решение СЛАУ средствами MS Excel 44
Решение СЛАУ средствами MS Excel 44
 Решение СЛАУ средствами MS Excel 45
Решение СЛАУ средствами MS Excel 45
 Решение СЛАУ средствами MS Excel 46
Решение СЛАУ средствами MS Excel 46
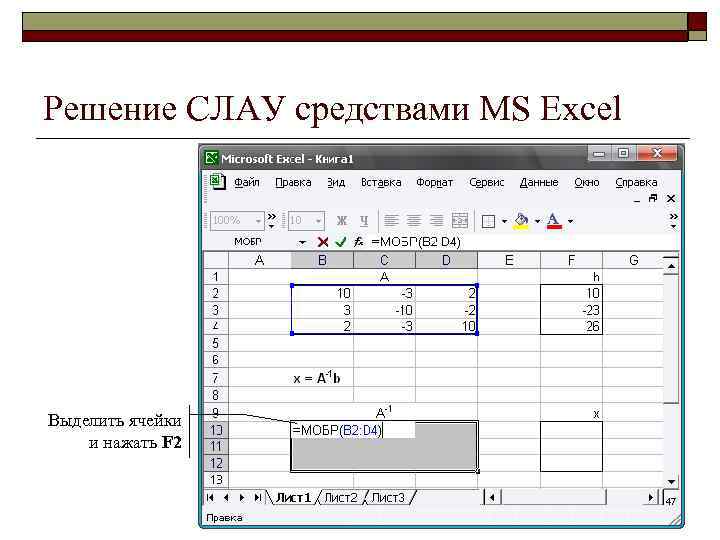 Решение СЛАУ средствами MS Excel Выделить ячейки и нажать F 2 47
Решение СЛАУ средствами MS Excel Выделить ячейки и нажать F 2 47
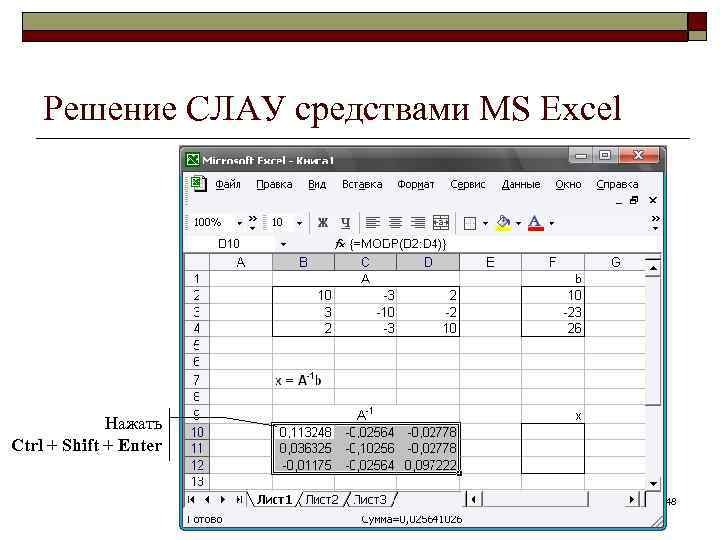 Решение СЛАУ средствами MS Excel Нажать Ctrl + Shift + Enter 48
Решение СЛАУ средствами MS Excel Нажать Ctrl + Shift + Enter 48
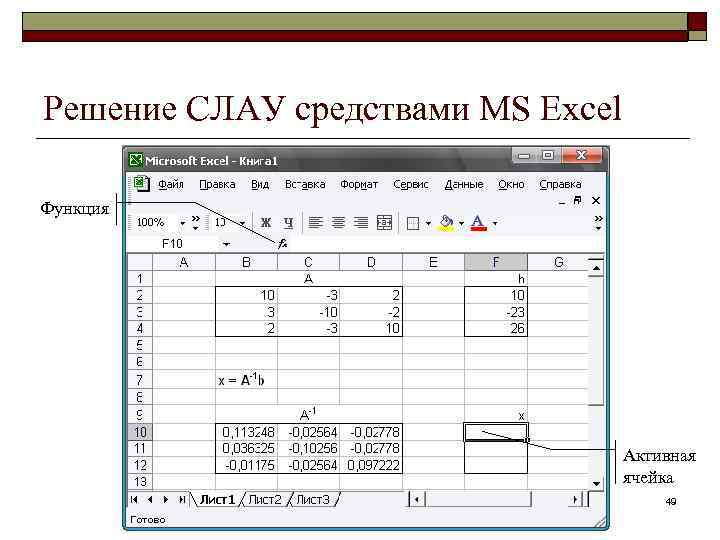 Решение СЛАУ средствами MS Excel Функция Активная ячейка 49
Решение СЛАУ средствами MS Excel Функция Активная ячейка 49
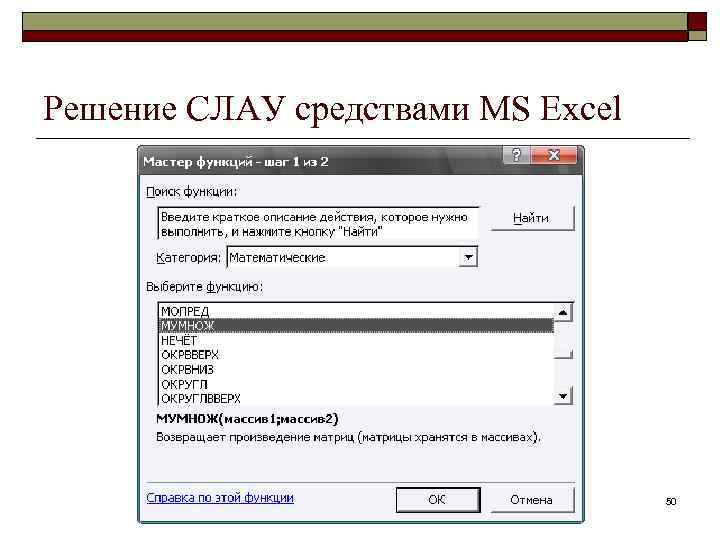 Решение СЛАУ средствами MS Excel 50
Решение СЛАУ средствами MS Excel 50
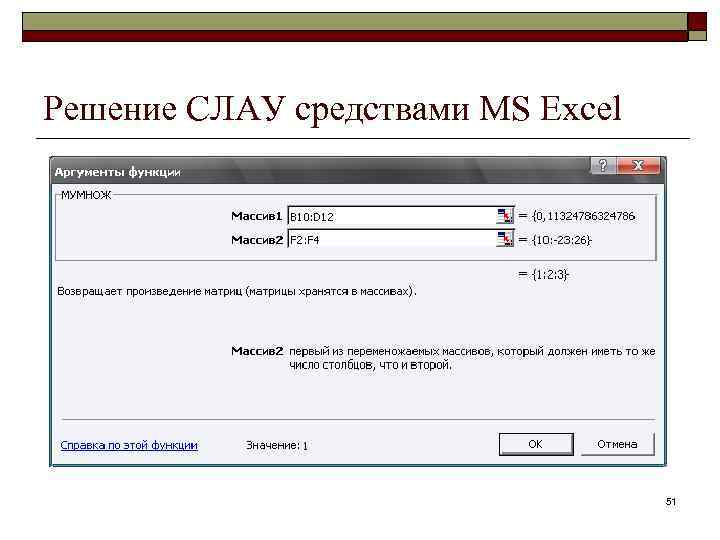 Решение СЛАУ средствами MS Excel 51
Решение СЛАУ средствами MS Excel 51
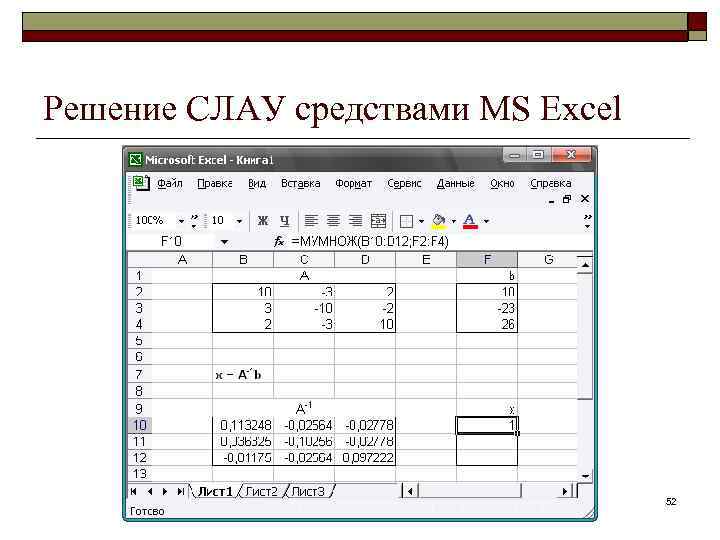 Решение СЛАУ средствами MS Excel 52
Решение СЛАУ средствами MS Excel 52
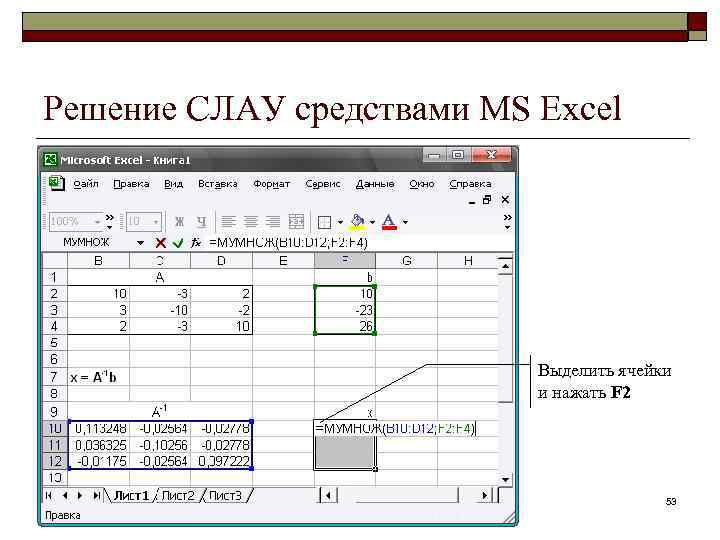 Решение СЛАУ средствами MS Excel Выделить ячейки и нажать F 2 53
Решение СЛАУ средствами MS Excel Выделить ячейки и нажать F 2 53
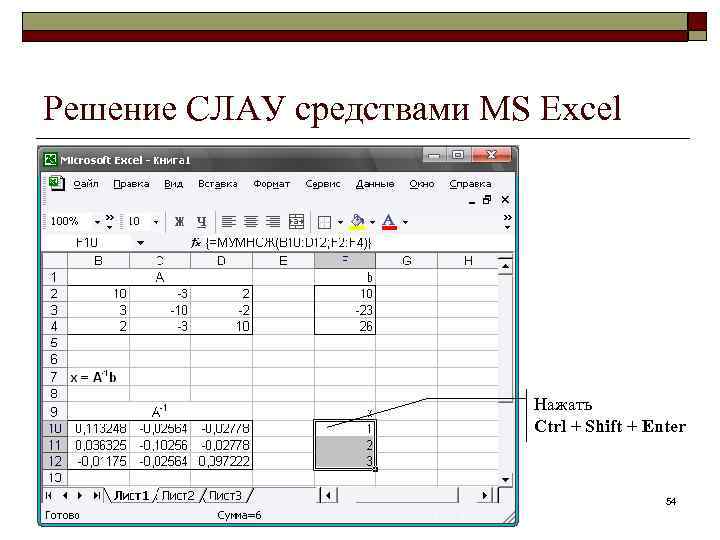 Решение СЛАУ средствами MS Excel Нажать Ctrl + Shift + Enter 54
Решение СЛАУ средствами MS Excel Нажать Ctrl + Shift + Enter 54
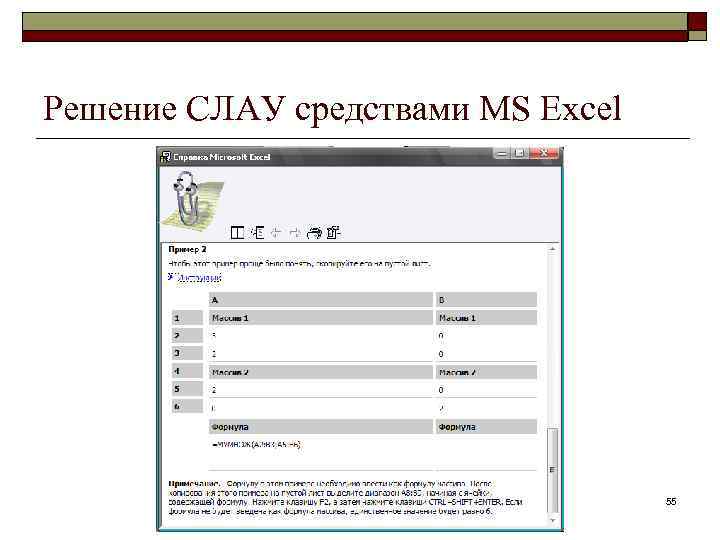 Решение СЛАУ средствами MS Excel 55
Решение СЛАУ средствами MS Excel 55


