L5-12.ppt
- Количество слайдов: 20

ВЫЧИСЛИТЕЛЬНАЯ АЭРОГИДРОДИНАМИКА Лекция 5 Уравнения гиперболического типа

Решение уравнений линейной акустики Физическая задача - процесс распространения звуковых волн в сжимаемой среде Характеристики физического процесса: Газ находится в состоянии покоя (скорость u=0) и характеризуется плотностью 0 , давлением p 0 и аддиабатической скоростью звука Процесс распространения звуковых волн в сжимаемой среде – это распространение малых возмущений давления и скорости, т. е. Выбор математической модели Процесс распространения звуковых волн описывают уравнения линейной акустики: Система уравнений одномерных изэнтропических движений газа в инвариантах Римана: + Общее решение , где f и g - произвольные функции, определяемые начальными условиями Решение описывает две бегущие волны, распространяющиеся по газу без искажения вправо и влево со скоростью звука c 0
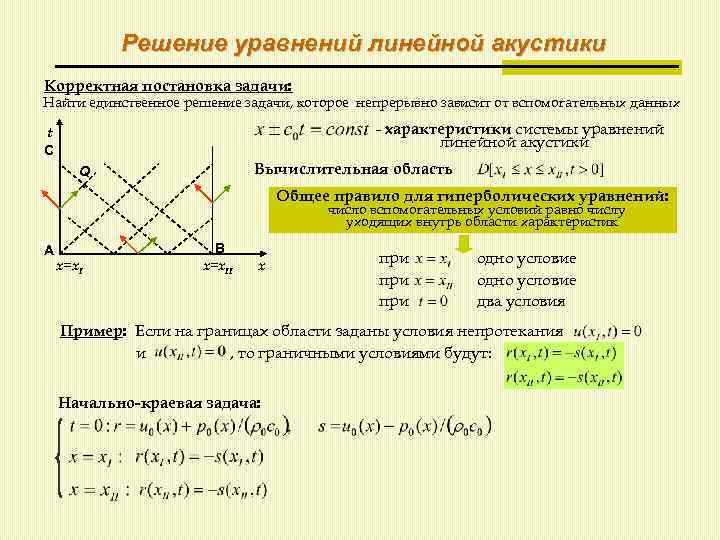
Решение уравнений линейной акустики Корректная постановка задачи: Найти единственное решение задачи, которое непрерывно зависит от вспомогательных данных - характеристики системы уравнений линейной акустики t C Вычислительная область Q Общее правило для гиперболических уравнений: число вспомогательных условий равно числу уходящих внутрь области характеристик A x=x. I B x=x. II x при при одно условие два условия Пример: Если на границах области заданы условия непротекания и , то граничными условиями будут: Начально-краевая задача:

Решение уравнений линейной акустики Дискретизация и выбор разностной схемы: - сеточные функции Алгоритм решения разностных уравнений 1) Для выбранной разностной схемы сначала решается первое уравнение 2) Из правого граничного условия определяется 3) Решается второе уравнение справа налево и значение на левой границе Тестирование – сравнение с аналитическим решением Общее решение системы уравнений линейной акустики: Начальные условия: на + Полученное аналитическое решение задачи сравниваем с численным решением

Задача о распаде разрыва - некоторые постоянные: или Разрывный характер начальных данных t C 0 - : x= x*-c 0 t s=const I r C 0+: x= x*+c 0 t r=const III s r s Вдоль характеристик постоянен риманов инвариант r, а вдоль характеристик -s В области I II В области I сохраняются невозмущенные “левые” величины В области II , т. е. сохраняются невозмущенные “правые” величины В области III величины u, p могут быть найдены из уравнений: u. I , p. I x* u. II, p. II Решение задачи. x дается следующими формулами: , если Функции имеют разрыв вдоль двух линий: и , разделяющих области I, III. Задача о распаде начального разрыва

Квазилинейные уравнения Линейные уравнения переноса Если коэффициент a зависит еще и от решения u, т. е. то уравнения называются квазилинейными Уравнение называется уравнением Хопфа Начально-краевая задача даже при гладких начальных данных и краевых условиях может не иметь гладких решений ,
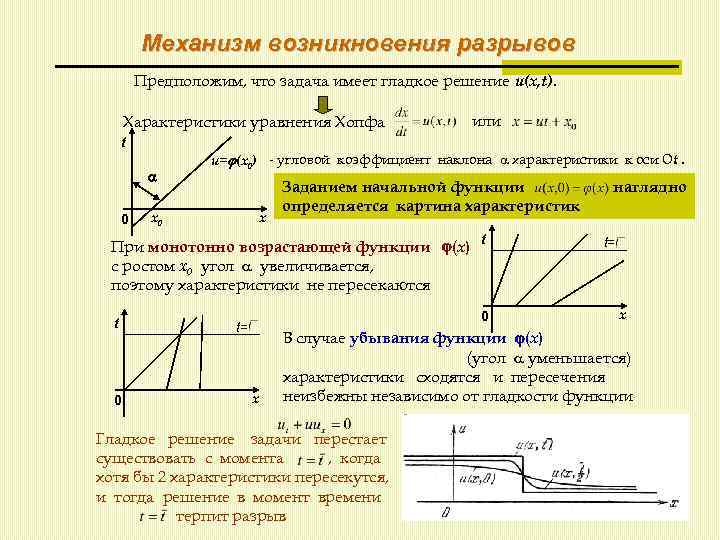
Механизм возникновения разрывов Предположим, что задача имеет гладкое решение u(x, t). Характеристики уравнения Хопфа или t 0 u= (x 0) - угловой коэффициент наклона характеристики к оси Оt. x x 0 Заданием начальной функции определяется картина характеристик При монотонно возрастающей функции (x) t с ростом x 0 угол увеличивается, поэтому характеристики не пересекаются t 0 0 t= x наглядно t= x В случае убывания функции (x) (угол уменьшается) характеристики сходятся и пересечения неизбежны независимо от гладкости функции Гладкое решение задачи перестает cуществовать с момента , когда хотя бы 2 характеристики пересекутся, и тогда решение в момент времени терпит разрыв

Обобщенные решения Для задач типа , не имеющих гладких решений , приходится расширить понятие решения и некоторым естественным способом ввести обобщенные решения, которые могут быть и разрывными Для этого существует 2 основных способа: 1 -ый состоит в том, чтобы записывать физические законы сохранения не в дифференциальной, а в интегральной форме. Тогда они имеют смысл и для разрывных функций, которые нельзя дифференцировать, но интегрировать можно; 2 -ой способ состоит в искусственном введении в дифференциальные уравнения таких членов, при которых эти уравнения имеют гладкие решения. Эти искусственно введенные члены в случае газодинамических задач имеют смысл малой вязкости, выглаживающей разрывы течения. Например, для уравнения Хопфа это будет. Член меняет тип гиперболического уравнения Хопфа на параболический, дающий гладкие решения. Затем коэффициент при “вязком” члене устремляют к 0 ( 0), а предел, к которому стремится решение, принимают за обобщенное решение задачи.

Разностные схемы для уравнения Хопфа 1. Явная схема Погрешность в т. ( Устойчивость условная ), ( ) 2. Неявная схема Погрешность в т. ( Устойчивость абсолютная 3. Двухшаговая схема Лакса-Вендроффа 1 -предиктор 2 -корректор Погрешность в т. ( Устойчивость условная )

Уравнения газовой динамики Аэродинамика летательных аппаратов Гидродинамика больших скоростей Газовая динамика Уравнения газовой динамики в дифференциальной форме (уравнения Эйлера невязкого сжимаемого газа): + 4 искомые функции

Уравнения газовой динамики Дивергентный вид Недивергентный вид Векторный вид -частные производные функции F , входящей в уравнение состояния Уравнения газовой динамики - система квазилинейных дифференциальных уравнений первого порядка

Гиперболичность уравнений Эйлера Фундаментальное свойство системы уравнений Эйлера состоит в ее гиперболичности и описывается с помощью характеристик 3 характеристики: Через такую характеристику газ не течет. Она отделяет одни частицы от других и, следовательно, в пространстве является геометрическим местом траекторий частиц. Эта характеристика называется контактной или энтропийной. Через такие характеристики газ течет, причем относительно характеристики по нормали к ней – со скоростью звука. Такие характеристики называются звуковыми.

Соотношения на разрыве W - любая подобласть с границей Г в плоскости (x, t), лежащая в области определения решения системы Эти соотношения сохраняют смысл также для разрывных решений По формуле Грина t x=x. S(t) (2) - уравнение линии разрыва и - скорость распространения разрыва (1) Контур Г в плоскости (x, t) такой, что его две линии близко примыкают к линии разрыва Г x Условия на линии разрыва решений уравнений газовой динамики как следствия интегральных законов сохранения: Условия Ренкина-Гюгонио в системе координат, движущейся вместе с разрывом со скоростью D, когда = u - D

Соотношения на разрыве Условия на линии разрыва решений уравнений газовой динамики поток массы вещества через разрыв 1. Разрывы с m=0 называются контактными. Через поверхность такого разрыва отсутствует поток вещества. 2. Разрывы с m 0 называются ударными волнами. Здесь все функции изменяются скачком. Представлением параметров в функции числа Маха перед скачком получаются формулы, связывающие величины до и после скачка (слева L и справа R)

Разностные схемы для уравнений Эйлера 1. Схема Лакса-Вендроффа 1 этап - предиктор схема Лакса 2 этап - корректор схема крест Погрешность аппроксимации Устойчивость условная . в точках . 2. Схема Маккормака 1 этап - предиктор схема «уголок» 2 этап - корректор схема «уголок» Погрешность аппроксимации Устойчивость условная . в точках .

Течение в сверхзвуковом сопле Сопло Лаваля Площадь сечения сопла A(x) Минимальное сечение с площадью A* , называемое критическим, расположено при x* Уравнения установившегося течения в сопле Лаваля в одномерной постановке: Со стороны стенок канала на газ действует сила давления, направленная в каждой точке по нормали к стенке канала. Эта сила имеет ненулевую составляющую в продольном направлении при

Метод установления – замена стационарной задачи на нестационарную с теми же краевыми условиями и получение ее предельного решения при : Векторно-матричный вид Интегрирование уравнений по t ведется до тех пор, пока не будет достигнут стационарный режим течения Критерий установления = условие, при выполнении которого итерационный процесс можно прекратить: невязка уравнения неразрывности Критерий сходимости станет более жестким, если потребовать малость невязок также и в уравнениях движения и энергии.
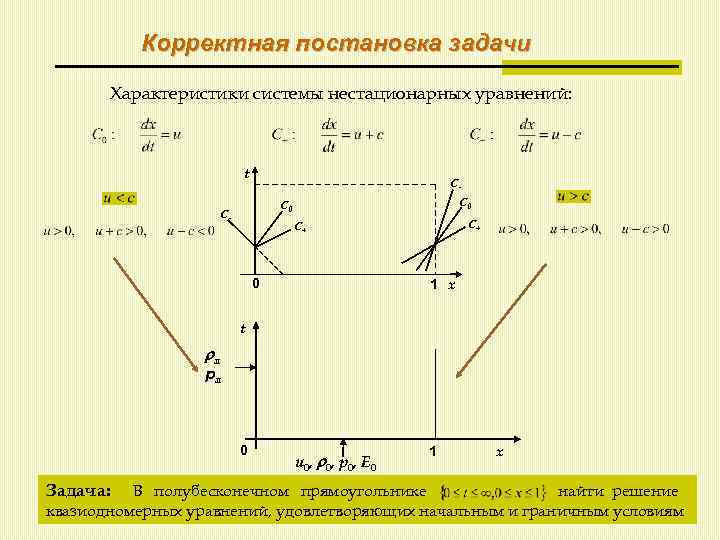
Корректная постановка задачи Характеристики системы нестационарных уравнений: t СС 0 С- С+ С+ 0 1 x t л pл 0 Задача: u 0, p 0, E 0 1 x В полубесконечном прямоугольнике найти решение квазиодномерных уравнений, удовлетворяющих начальным и граничным условиям

Точные решения Задача о нестационарном движении сжимаемого газа в сопле не имеет аналитического решения, но при установлении течения распределение параметров в сопле получено: Точное решение уравнений задано в параметрическом виде, где роль параметра играет число Маха М ( ) Формулы связи между скоростью, давлением и плотностью в изэнтропическом адиабатическом движении

Нахождение точного решения, заданного в параметрическом виде Гладкое течение в сопле Разрывное течение в сопле Задаем 0 и p 0 на входе в канал, а также площадь сечения A(x). В критическом сечении x M =1; 2. Из (*), полагая , находим число Маха M 0 во входном сечении, причем M 0<1; 3. По известным 0, p 0, M 0 из соотношения находим скорость u 0 во входном сечении; 4. Из (**), полагая , находим число Маха в любом сечении x , причем M<1 при x<x и M>1 при ; 1. 5. По (**) находим , u, p при 5. По (**) находим L, u. L, p. L при ; 6. Зная L , u. L , p. L , по соотношеням на скачке, находим R , u. R , p. R ; 7. По (*), полагая и т. д. , находим число Маха в любом сечении канала после скачка (M<1); 8. По (**) находим , u, p при. 1. . Задаем 0 и p 0 на входе в канал, а также площадь сечения A(x). В критическом сечении x M =1; 2. Из (*), полагая , находим ! число Маха M 0 во входном сечении, причем M 0<1; 3. По известным 0, p 0, M 0 из соотношения находим 4. Из (*), полагая , находим число Маха в любом сечении , и M<1 при x<x и M>1 при ;
L5-12.ppt