L4-12.ppt
- Количество слайдов: 19

ВЫЧИСЛИТЕЛЬНАЯ АЭРОГИДРОДИНАМИКА Лекция 4 Уравнения гиперболического типа

Уравнение переноса Процессы, связанные с переносом массы, импульса и энергии Линейное одномерное уравнение переноса -характеристики, вдоль которых Характеристическое уравнение Задача: Найти решение уравнения переноса при заданном начальном условии на отрезке a=const > 0 t Условие постоянства решения вдоль характеристики для линейного уравнения переноса Вид функции g определен начальными условиями, и решение в произвольный момент времени представляет первоначальный профиль переменной u, перемещающийся в виде волны вдоль оси x со скоростью а, т. е. перенос некоторой субстанции u потоком с постоянной скоростью а. II 0 I (x 1, t 1) b В области II решение не определено Чтобы обеспечить единственность решения необходимо задать на левой границе x=0 граничное условие ! x Общее правило для гиперболических уравнений: для корректности задачи число вспомогательных условий равно числу характеристик, направленных внутрь рассматриваемой области (уходящих)
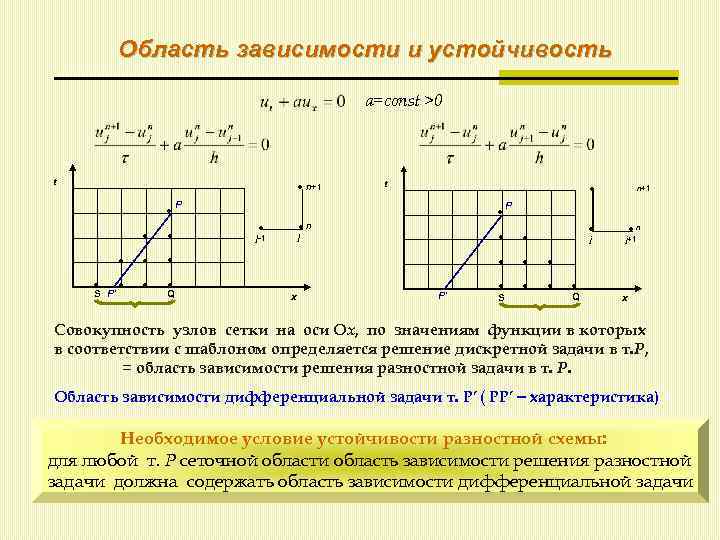
Область зависимости и устойчивость a=const >0 t n+1 t P Q n S P′ P P′ x n j j-1 n+1 S j Q j+1 x Совокупность узлов сетки на оси Ox, по значениям функции в которых в соответствии с шаблоном определяется решение дискретной задачи в т. P, = область зависимости решения разностной задачи в т. P. Oбласть зависимости дифференциальной задачи т. P’ ( PP’ характеристика) Необходимое условие устойчивости разностной схемы: для любой т. P сеточной области область зависимости решения разностной задачи должна содержать область зависимости дифференциальной задачи

Явные и неявные разностные схемы a=const >0 -предыдущий временной слой явная форма для вычисления сеточных значений решения на следующем временном слое явная разностная схема неявная разностная схема Разностные схемы, содержащие более чем одно значение сеточного решения на слое n+1 , называются неявными.

Явные разностные схемы 1) Явные схемы бегущего счета для a=const <0 для a=const >0 Погрешность аппроксимации в точках ; Устойчивость условная: 2) Гибридная схема ( учитывает знакопеременность a ) Погрешность аппроксимации Устойчивость условная: в точках ;

Явные разностные схемы 3) Схема Лакса ( центральные разности ) порядок аппроксимации не понятен погрешность аппроксимации Функция такова, что при h 0 и будет 0 - закон предельного перехода Аппроксимация вида при , погрешность которой стремится к нулю при любом законе стремления шагов к нулю, называется безусловной или абсолютной. Если же погрешность аппроксимации стремится к нулю при одних законах убывания и не стремится при других, то аппроксимацию называют условной. При законе предельного перехода схема Лакса аппроксимирует уравнение параболического типа Погрешность аппроксимации Устойчивость условная: в точках при условии ;

Явные разностные схемы 4) Схема «крест» = схема с перешагиванием = «чехарда» n+1 j-1 j+1 n-1 Погрешность аппроксимации в точках ; Устойчивость условная: Схема является трехслойной и строит решение по двум предыдущим временным слоям. При ее применении возникают проблемы с началом вычислений, которое должно осуществляться каким-либо другим методом. Использование схем типа “уголок”. Это эквивалентно использованию дополнительного узла разностной сетки , лежащего вне сеточной области, значение сеточной функции в котором определяется линейной интерполяцией: для схем первого порядка аппроксимации по x для схем второго порядка аппроксимации по x Порядок погрешности аппроксимации схемы, применяемой в граничном узле, не должен быть ниже порядка погрешности аппроксимации схемы для внутренних узлов

Явные разностные схемы 5) Схема Лакса-Вендроффа (с пересчетом) этап предиктора по схеме Лакса j-1 j+1/2 n+1/2 n j этап корректора n+1 по схеме “крест” j-1/2 j+1/2 n На первом этапе обеспечивается выполнение условий устойчивости, а на втором – выполнение требуемой точности. Погрешность аппроксимации в точках Устойчивость условная: ;

Явные разностные схемы 6) Схема Мак-Кормака (двухшаговая) этап предиктора по схеме «уголок» этап корректора по схеме «уголок» Добавление на этапе корректора второй разности обеспечивает повышение порядка точности. Погрешность аппроксимации в точках ; Устойчивость условная: Схема не использует полуцелых узлов и легко программируется, чередование “уголков” на этапах предиктора и корректора может быть обратным (это полезно для задач с движущимися разрывами).

Явные разностные схемы Простейшие явные схемы накладывают существенное ограничение на временной шаг : . Cемействo явных схем с расширенными интервалами устойчивости: схемы типа Рунге-Кутты Замена оператора пространственного дифференцирования разностным оператором: Решение ОДУ m-стадийная схема Рунге-Кутты: Значения коэффициентов подбираются из двух требований: 1) аппроксимации исходного уравнения, 2) максимально возможного интервала устойчивости: Условия устойчивости:

Явные разностные схемы Эффективность реализации схем C - максимальное число Куранта, допускаемое устойчивостью схемы, N – число требуемых вычислений значений оператора Pu. Для схем Рунге-Кутты: Для схемы Мак-Кормака: 2 вычисления Pu +

Неявные разностные схемы 1) Неявные схемы бегущего счета для a=const <0 для a=const >0 Погрешность аппроксимации Устойчивость абсолютная в точках ; 2) Неявная гибридная схема ( учитывает знакопеременность a ) Погрешность аппроксимации Устойчивость абсолютная в точках ; 3) Неявная двухшаговая схема этап предиктора по неявной схеме бегущего счета этап корректора по схеме “крест” Погрешность аппроксимации Устойчивость абсолютная в точках ;

Основные этапы решения задачи на компьютере 1. Постановка проблемы (цель); 2. Выбор и построение математической модели (гипотезы, выбор ДУЧП и т. д. ); 3. Постановка вычислительной задачи (дискретизация, выбор разностной схемы); 4. Предварительный (предмашинный) анализ свойств вычислительной задачи (анализ корректности ее постановки, исследование устойчивости решения к погрешностям); 5. Выбор и построение численного метода (чаще выбор среди известных численных методов по критериям их качества для решения данной задачи наиболее эффективным образом); 6. Алгоритмизация и программирование (численный метод содержит только принципиальную схему решения задачи, необходима подробная детализация этапов вычислений для того, чтобы получить реализуемый на ЭВМ алгоритм); 7. Отладка программы (устранение ошибок программирования, тестирование программы); 8. Счет по программе (многоразовый); 9. Обработка и интерпретация результатов (представление в виде таблиц, графиков, фильмов, оценка достоверности результатов).

Тестирование программы Решение “бегущая полочка” или “бегущая ступенька”: несогласованные начальные и краевые условия Уравнения характеристик имеют вид x - at = const , вдоль характеристик функция u(x, t) постоянна. Характеристика x-at=0 , a>0 делит область решения на две подобласти и является линией, вдоль которой распространяется разрыв функции u(x, t): t x=at C 2 C 1 x 0 Точное решение задачи: u C 2 C 1 “полочка”, бегущая слева направо со скоростью а 0 x 0=at 0 x
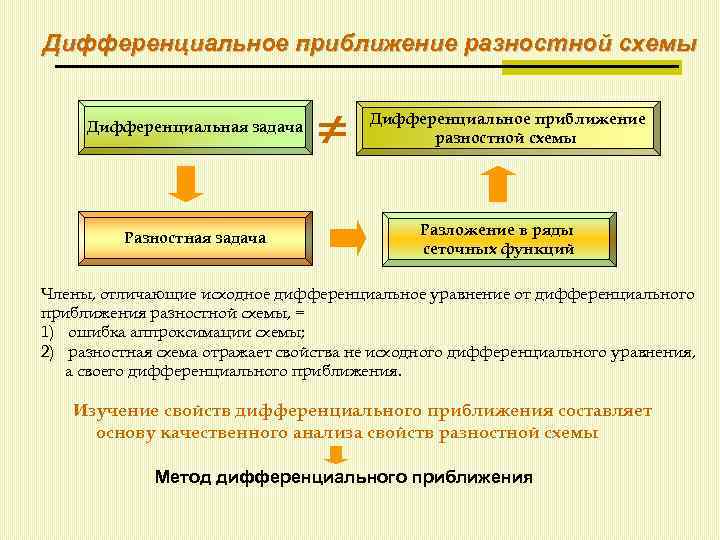
Дифференциальное приближение разностной схемы Дифференциальная задача Разностная задача Дифференциальное приближение разностной схемы Разложение в ряды сеточных функций Члены, отличающие исходное дифференциальное уравнение от дифференциального приближения разностной схемы, = 1) ошибка аппроксимации схемы; 2) разностная схема отражает свойства не исходного дифференциального уравнения, а своего дифференциального приближения. Изучение свойств дифференциального приближения составляет основу качественного анализа свойств разностной схемы Метод дифференциального приближения

Дифференциальное приближение разностной схемы Явная схема бегущего счета a=const >0 Разложим все члены разностной схемы в ряд Тейлора, а затем ограничимся в бесконечных разложениях членами с младшим порядком по шагам сетки. Укороченное таким образом соотношение называется первым дифференциальным приближением (п. д. п. ) разностной схемы. П. д. п схемы “уголок” содержит производные по времени и по пространству Г-форма п. д. п. Продифференцируем Г-форму п. д. п. схемы “уголок” по t и x: П. д. п схемы “уголок” без производных по t П-форма п. д. п. – параболическое уравнение сглаживает разрыв Правая часть П-формы п. д. п. = 0 схема “уголок” точно аппроксимирует уравнение переноса (с -ым порядком по и h ) не сглаживает разрыв Свойство схемы сохранять разрыв (не сглаживать его) называется К-свойством.

Условие устойчивости Куранта-Фридрихса-Леви - условие устойчивости схемы “уголок” u u K=1, 02 x K=0, 995 x - условие устойчивости Куранта-Фридрихса-Леви применимо ко всем явным схемам для ДУЧП гиперболического типа С физической точки зрения условие КФЛ означает, что частица жидкости За один шаг по времени t не должна продвигаться более, чем на один пространственный шаг x. П-форма п. д. п. явной схемы “уголок” П-форма п. д. п. неявной схемы “уголок” Неявная схема в раз сильнее размазывает “полочку”, чем явная

Тестирование программы Проведение расчетов на последовательности измельчающихся сеток Погрешность численного решения будет уменьшаться по вполне определенному закону, зависящему от порядка аппроксимации При тестировании программы на “бегущей полочке”, описываемой разрывной функцией, максимальное отклонение численного решения от точного независимо от значений и h может быть величиной порядка половины скачка, т. к. численное решение сглаживает “полочку”, размазывая разрыв При теоретической погрешности , полученной в предположении гладкости решения дифференциальной задачи, реальная погрешность есть величина для разрывного решения

Линейные уравнения с переменными коэффициентами Пусть коэффициент a=a(x, t) уравнения переноса непрерывен в области. Если a(x, t) - знакопостоянная функция в , то постановка задачи совпадает с постановкой задачи для уравнения переноса с постоянным коэффициентом a=const. При знакопеременной функции a(x, t) может измениться формулировка краевых условий: 1) В этом случае краевые условия не задаются. Т. к. в силу непрерывности функции a(x, t) найдется точка x* такая, что a(x*, t) = 0, 0 < x* < X, а из уравнения при x=x* следует ut = f(x*, t) формула для определения u(x*, t). Т. о. имеем граничное условие для решения задачи. 2) Здесь задаются 2 краевых условия: Для линейных уравнений с переменными коэффициентами возможно использование любой из рассматриваемых ранее схем с учетом области знакопостоянства коэффициента a(x, t) и с необходимыми изменениями в реализации краевых условий. Наиболее удобны схемы, автоматически учитывающие знак a(x, t)
L4-12.ppt