ВЫЧИСЛИТЕЛЬНАЯ АЭРОГИДРОДИНАМИКА Лекция 2 Определяющие уравнения ВАГД

ВЫЧИСЛИТЕЛЬНАЯ АЭРОГИДРОДИНАМИКА Лекция 2 Определяющие уравнения ВАГД

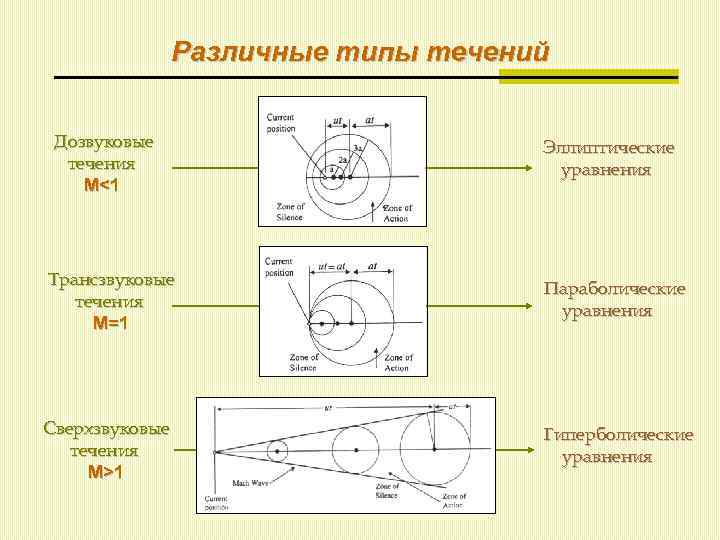Различные типы течений Дозвуковые течения М<1 Эллиптические уравнения Трансзвуковые течения М=1 Параболические уравнения Сверхзвуковые течения М>1 Гиперболические уравнения

Математическая классификация уравнений Дифференциальные уравнения 2 -ого порядка: 1) Коэффициенты A, B, C, D, F зависят от переменных x, y, u, ux, uy, − нелинейное уравнение; 2) A, B, C, D, F не зависят от переменных x, y, u − линейное уравнение с постоянными коэффициентами; 3) A=A(x, y), B=B(x, y), C=C(x, y), D=D(x, y) и F=F(x, y, u) − линейное уравнение с переменными коэффициентами; 4) A=A(x, y, u), B=B(x, y, u), C=C(x, y, u), D=D(x, y, u) и F=F(x, y, u) и линейно от u − квазилинейное уравнение; 5) A= B=C=0, D 0, E 0 − уравнение первого порядка − уравнение переноса.

Математическая классификация уравнений По коэффициентам при высших производных = по знаку дискриминанта d=B 2 -AC • d > 0 уравнение гиперболическое каноническая форма uxx – uyy = h(ux, uy, u, x, y) • d < 0 уравнение эллиптическое каноническая форма uxx + uyy = h(ux, uy, u, x, y) • d = 0 уравнение параболическое каноническая форма uxx = h(ux, uy, u, x, y) Квадратичная форма каноническая форма: гипербола эллипс парабола

Классификация с помощью характеристик На линии y=y(x) заданы значения: y O Можно ли, зная значения функции и ее первых производных на кривой y(x), установить значения функции в точках, соседних с этой кривой? известны из начальных данных y(x) u( ) p( ) q( ) x M y x Задача Коши для уравнения производные неизвестны Приращения первых производных вдоль кривой Исходное уравнение Линейная система для значений вторых производных в точке М кривой y(x) Угловой коэффициент кривой Единственное решение для вторых производных Определитель системы 0

Классификация с помощью характеристик Определитель системы = 0 Характеристики Наличие характеристик определяет тип уравнения > 0 уравнение гиперболического типа 2 вещественные характеристики = 0 уравнение параболического типа 1 вещественная характеристика < 0 уравнение эллиптического типа нет вещественных характеристик Физический смысл характеристик: характеристики определяют область влияния точек

Физические задачи ДУЧП 1) Различные процессы колебания (струны, стержня, пружины, мембраны или электрические колебания в проводах) известное волновое уравнение 2) Процессы теплопроводности и диффузии уравнения параболического типа 3) Стационарные процессы колебаний, теплопроводности и др. уравнения эллиптического типа уравнение Лапласа

Модельные уравнения Простейшее уравнение переноса, моделирующее конвективный перенос Невязкое уравнение Бюргерса распространение нелинейных волн в одномерном случае Уравнение Бюргерса уравнения газовой динамики Уравнение Пуассона распределение температуры в твердом теле, когда внутри тела есть источники тепла интенсивности f Уравнение одномерной нестационарной теплопроводности движение вязкой жидкости в пограничном слое тела и др. Двумерное уравнение нестационарной теплопроводности Одномерное уравнение теплопроводности с конвекцией , моделирующее сочетание конвективных и диффузионных механизмов переноса Волновое уравнение распространение колебаний в сплошных средах и др.

Физическая классификация уравнений 1. Стационарные задачи Задача называется стационарной, если решение ДУЧП внутри некоторой области определяется лишь условиями на границе этой области определение стационарного поля температур, расчет течения несжимаемой невязкой жидкости, нахождение упругих напряжений в твердом теле B D Установившиеся процессы описываются ДУЧП эллиптического типа 2. Маршевые задачи Маршевой или эволюционной называется задача, в которой требуется найти решение ДУЧП в незамкнутой области при заданных граничных и начальных условиях нестационарное распространение тепла, t или y задачи колебания (волновое уравнение), нестационарные течения невязкой жидкости, D стационарные сверхзвуковые течения невязкого газа, B B пограничный слой B x ДУЧП гиперболического и параболического типа

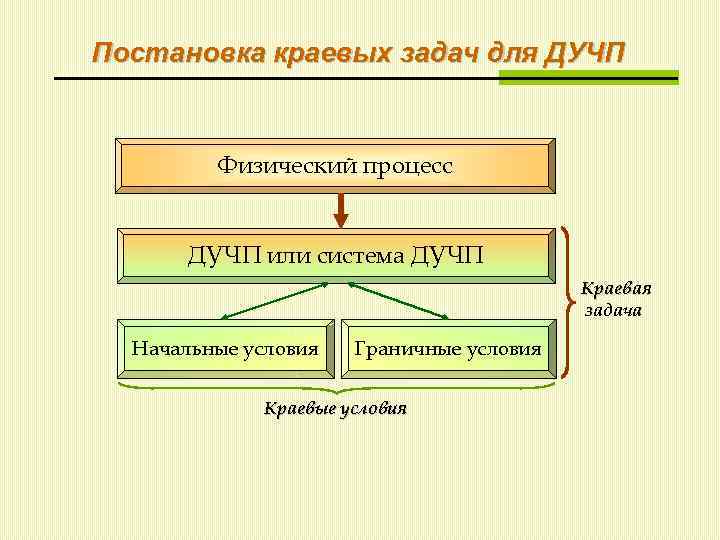Постановка краевых задач для ДУЧП Физический процесс ДУЧП или система ДУЧП Краевая задача Начальные условия Граничные условия Краевые условия

Постановка краевых задач для ДУЧП Типы краевых задач 1. Задача Типы граничных условий Коши для уравнений гиперболического и параболического типов: задаются начальные условия, граничные условия отсутствуют; I. Граничное условие I рода 2. Краевая задача границе области задано значение производной искомого решения по нормали к этой границе du/dn; для уравнений эллиптического типа: граничные условия задаются на всех границах области, начальные условия отсутствуют; 3. Смешанная задача для уравнений гиперболического и параболического типов: задаются начальные и граничные условия – на границе задано значение искомой функции u; II. Граничное условие II рода – на III. Граничное условие III рода, выражающее закон теплообмена Ньютона: тепловой поток через границу тела пропорционален разности температур между телом и окружающей его средой

Корректно поставленная задача Постулат Адамара: все процессы в природе связаны Адамара с корректными задачами Краевая задача является математически корректно поставленной, если выполняются следующие условия: 1) решение задачи существует, 2) решение является единственным, 3) решение непрерывно зависит от вспомогательных данных 2) Неединственность = несоответствие вспомогательных условий типу определяющего ДУЧП 3) = Требование, чтобы малое изменение начальных или граничных условий влекло за собой лишь малое изменение решения Требование корректности важно для построения вычислительных методов: необходима их устойчивость как к малым ошибкам в исходных данных, так и к ошибкам, возникающим при проведении вычислений (ошибкам округления)

Корректно поставленная задача Решить уравнение Лапласа с заданными при , граничными условиями Метод разделения переменных Решение при больших n решение u т. е. неограниченный рост Но , непрерывность по начальным данным отсутствует при больших n мало непрерывность по граничным данным отсутствует Анализ свойств ДУЧП: Уравнение Лапласа эллиптическое , Решение зависит от условий на всей границе замкнутой области Но открытая область и граничные условия заданы лишь на Задача поставлена некорректно