ВЫЧИСЛИТЕЛЬНАЯ АЭРОГИДРОДИНАМИКА Курс лекций Поплавская Т В Д

ВЫЧИСЛИТЕЛЬНАЯ АЭРОГИДРОДИНАМИКА Курс лекций Поплавская Т. В. Д. ф. -м. н. , Внс ИТПМ профессор ФФ НГУ

Задачи курса l l l Обучение базовым (классическим) методам, используемым при математическом моделировании; Обучение выбору и использованию схем для решения задач математической физики; Решение конкретных вычислительных работ на компьютере.

Программа курса l l l Физические задачи, приводящие к дифференциальным уравнениям в частных производных. Методы решения уравнений математической физики. Теория разностных схем. Аппроксимация, устойчивость сходимость. Разностные методы решения уравнений гиперболического типа. Уравнения переноса. Линейные уравнения, квазилинейные уравнения, система уравнений линейной акустики. Явные и неявные схемы. Механизм возникновения разрывов. Обобщенное решение. Уравнения газовой динамики. Корректность постановки задачи. Схемы расщепления (по физическим процессам, предиктор-корректор). Численная диссипация и дисперсия. Монотонность разностных схем (схема “распад разрыва” С. К. Годунова). Приемы мотонизации. TVD-схемы. Квазиодномерное течение в канале переменного сечения. Метод установления. Точные решения для квазиодномерных уравнений газовой динамики. Методы расчета течений невязкого газа при наличии разрывов. Условия Ренкина-Гюгонио. Метод характеристик. Однородные и гибридные разностные схемы. Метод псевдовязкости. Ложная сходимость. Консервативные схемы. Дифференциальный анализатор ударных волн. Методы решения стационарных задач. Явные схемы с расширенными интервалами устойчивости. Схемы Рунге-Кутты. Разностные методы решения уравнений параболического типа. Качественные особенности решений параболических уравнений. Метод прогонки. Схема продольно-поперечной прогонки, стабилизирующей поправки. Однородные и дивергентные разностные схемы. Нелинейные параболические уравнения. Итерационные методы решения. Уравнения пограничного слоя. Разностные методы решения уравнений эллиптического типа. Типы краевых задач. Принцип максимального значения. Единственность и устойчивость. Некоторые точные решения.

Итоговый контроль: дифференцированный зачет – – оценка за семестровую контрольную работу; оценка, выставляемая преподавателем за работу в семестре с учетом своевременной сдачи заданий, посещаемости и активности на занятиях; оценка за выполнение заданий компьютерного спецпрактикума (отчет в письменной форме); оценка на зачете.

ВЫЧИСЛИТЕЛЬНАЯ АЭРОГИДРОДИНАМИКА Лекция 1 Введение

Что такое вычислительная аэрогидродинамика? l Сэр Исаак Ньютон 1643 -1727 Теоретическая построение и решение определяющих уравнений, пригодных для различных типов течения жидкости и газа и даже плазмы, получение точных аналитических решений этих уравнений, изучение разного рода аппроксимаций по отношению к этим уравнениям ГИДРОДИНАМИКА l Экспериментальная получение новой информации о свойствах потоков для построения физических моделей, проверка справедливости и установление пределов пригодности различных аппроксимаций по отношению к определяющим уравнениям

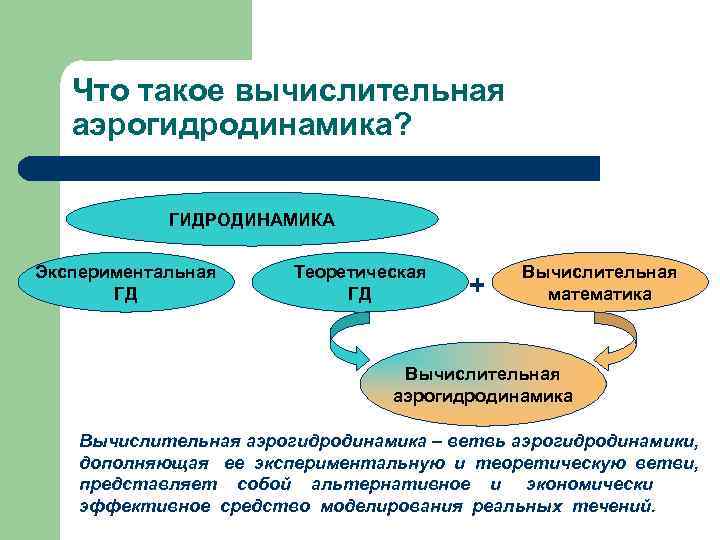Что такое вычислительная аэрогидродинамика? ГИДРОДИНАМИКА Экспериментальная ГД Теоретическая ГД + Вычислительная математика Вычислительная аэрогидродинамика – ветвь аэрогидродинамики, дополняющая ее экспериментальную и теоретическую ветви, представляет собой альтернативное и экономически эффективное средство моделирования реальных течений.

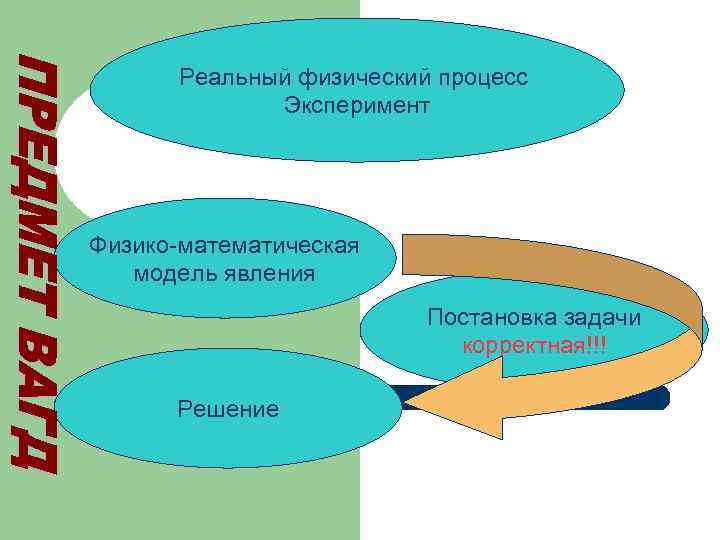Реальный физический процесс Эксперимент Физико-математическая модель явления Постановка задачи корректная!!! Решение

Этапы математического моделирования 1. Физическая постановка задачи. 2. Математическая постановка задачи. 3. Выбор численного метода. 4. Реализация метода. 5. Тестирование.

Преимущества вычислительной аэрогидродинамики l l l возможность моделирования условий течений, трудновоспроизводимых в эксперименте; позволяет получить более широкую и подробную информацию; стоимостная эффективность по сравнению с испытаниями в аэродинамических трубах. Численный эксперимент никогда и ни в коей мере не может заменить ни физический эксперимент, ни теоретический анализ

Список литературы 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. Роуч П. Вычислительная гидродинамика. – М. ; Мир, 1980. Андерсон Д. , Таннехил Дж, Плетчер Р. Вычислительная гидромеханика и теплообмен (2 тома). – М. ; Мир, 1990. Флетчер К. Вычислительные методы в динамике жидкостей (2 тома). – М. ; Мир, 1991. Chung T. J. Computational Fluid Dynamics. – Cambridge Univ. Press, 2002. Anderson J. D. Hypersonic and high temperature gas dynamics. – Published by AIAA Inc: Reston, Virginia, 2006. Поттер Д. Вычислительные методы в физике. – М. : Мир, 1975. Федоренко Р. П. Введение в вычислительную физику. – М. ; МФТИ, 1994. Тихонов А. Н. , Самарский А. А. Уравнения математической физики. – Москва 1953. Самарский А. А. Введение в теорию разностных схем. – М. : Наука, 1971. Годунов С. К. Численное решение многомерных задач газовой динамики. М. : Наука, 1976. Годунов С. К. , Рябенький В. С. Разностные схемы. – М. : Наука, 1977. Рождественский Б. Л. , Яненко Н. Н. Системы квазилинейных уравнений. – Москва. : Наука, 1978. Глава 3. Ковеня В. М. , Яненко Н. Н. Методы расщепления в задачах газовой динамики. – Новосибирск: Наука, 1981. Ворожцов Е. В. , Яненко Н. Н. Методы локализации особенностей при численном решении задач газодинамики. –Новосибирск: Наука, 1985.

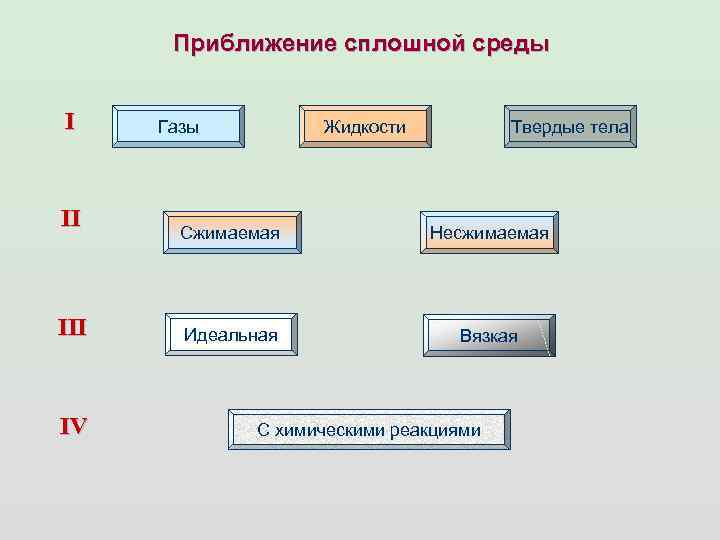Приближение сплошной среды I II IV Газы Жидкости Твердые тела Сжимаемая Несжимаемая Идеальная Вязкая С химическими реакциями

Определяющие уравнения модели сплошной среды – нестационарные уравнения Навье-Стокса Векторный вид для несжимаемой жидкости: (*) - вектор массовых сил, - элементы тензора скоростей деформаций, - диссипативная функция

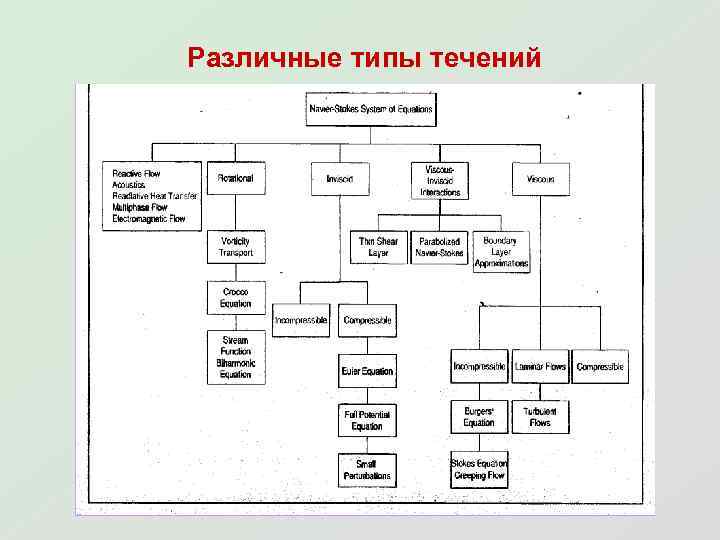Различные типы течений

Упрощенные модели Задача: Обтекание плоской пластины сверхзвуковым потоком газа - число Рейнольдса в реальных условиях при полетах ~ 106 ÷ 108 УВ возмущенный поток U∞>c пограничный слой

Уравнения движения идеальной жидкости = уравнения Эйлера Уравнения Эйлера описывают движение возмущенного невязкого течения. Это уравнения гиперболического типа.

Уравнения пограничного слоя Это уравнения параболического типа. Когда и уравнение энергии отсутствует, получаются известные уравнения Прандтля. Задача Блазиуса (диссер. 1908 г) = автомодельный несжимаемый пограничный слой на плоской полубесконечной пластине = тестовый пример для проверки правильности расчетов.

Уравнения полного вязкого ударного слоя Уравнения ПВУС включают в себя все члены уравнений ПС и уравнений Эйлера. Это уравнения параболического типа.

ВЫЧИСЛИТЕЛЬНАЯ АЭРОГИДРОДИНАМИКА - эффективное средство моделирования реальных явлений