Вычисление определенных интегралов

Вычисление определенных интегралов 1

Постановка задачи: вычислить интеграл вида где a и b – нижний и верхний пределы интегрирования; f(x) – непрерывная функция на отрезке [a, b]. 2

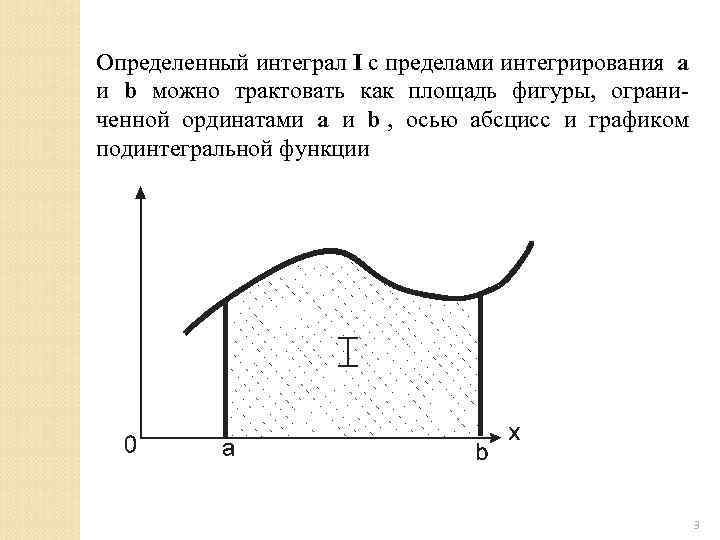Определенный интеграл I с пределами интегрирования a и b можно трактовать как площадь фигуры, ограни- ченной ординатами a и b , осью абсцисс и графиком подинтегральной функции 3

Обыкновенный определенный интеграл у которого известна его первообразная f(x) вычисляется по формуле I=f(b) – f(a). Численное интегрирование применяется в случае, когда вычисление функции сложно или невозможно. Обычно отрезок разбивается на части, к каждой из которых применяется простая формула. 4

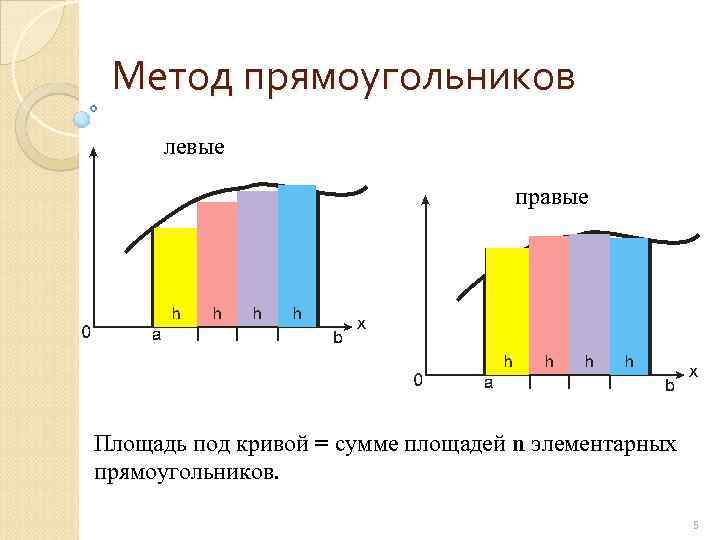Метод прямоугольников левые правые Площадь под кривой = сумме площадей n элементарных прямоугольников. 5

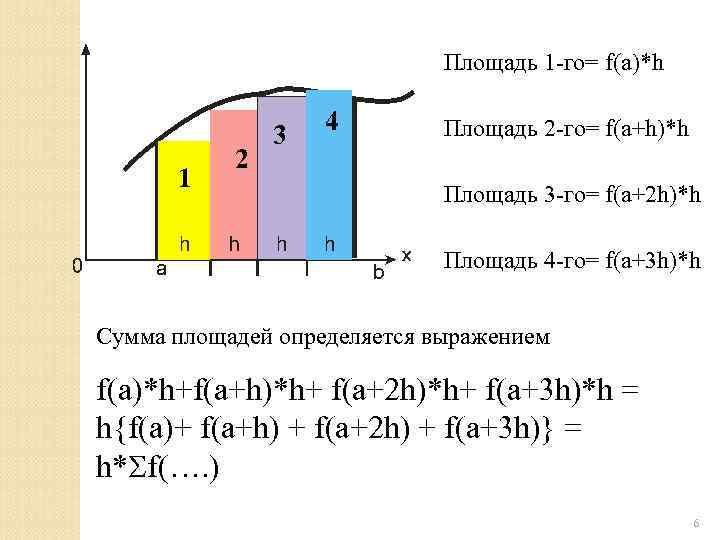Площадь 1 -го= f(a)*h 4 Площадь 2 -го= f(a+h)*h 3 2 1 Площадь 3 -го= f(a+2 h)*h Площадь 4 -го= f(a+3 h)*h Сумма площадей определяется выражением f(a)*h+f(a+h)*h+ f(a+2 h)*h+ f(a+3 h)*h = h{f(a)+ f(a+h) + f(a+2 h) + f(a+3 h)} = h* f(…. ) 6

Метод левых и средних прямоугольников n – количество отрезков 7

Метод правых прямоугольников 8

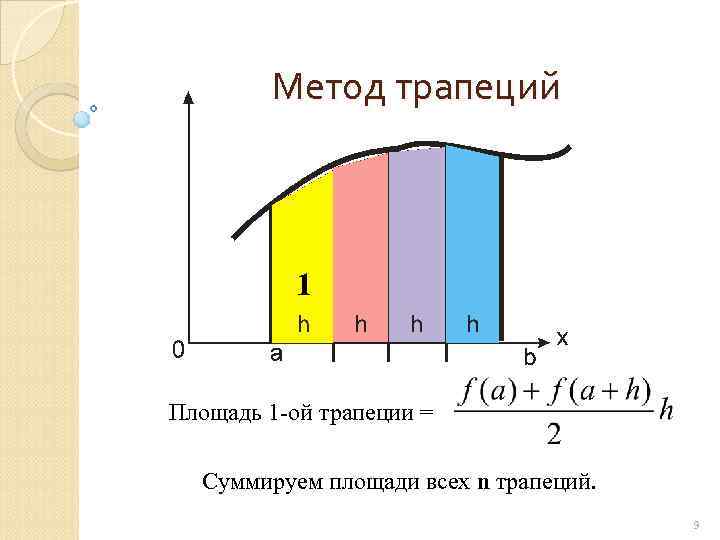Метод трапеций 1 Площадь 1 -ой трапеции = Суммируем площади всех n трапеций. 9

Метод трапеций 10

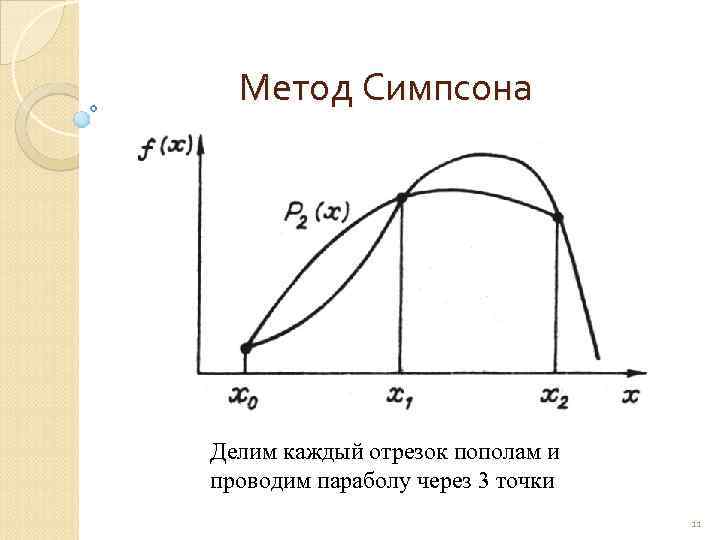Метод Симпсона Делим каждый отрезок пополам и проводим параболу через 3 точки 11

Метод Симпсона 12

Для вычисления интеграла любым методом необходимо: • разделить отрезок интегрирования на n частей (чем больше n, тем точнее); • вычислить значение интеграла с заданной точностью, т. е. n-е значение отличается от n+1–го на величину не более заданной точности. 13

Лабораторная работа № 4 Варианты заданий – сборник Арсеньев С. С. и др. стр. 41 -43. Вычислить заданный интеграл 5 -ю методами приближенно с точностью ε = 10 -4 при n = 10, 20, 30, 40. Примечание: в каждом из пунктов задания провести сравнение результатов вычисления с точным значением интеграла, приведенным в варианте задания. В задачах, содержащих параметры k, σ, вычисления провести для k = 1, 2, 3, 4, 5; - 0. 9 ≤ σ ≤ 0. 9, Δ σ = 0. 1. Сравнить полученные результаты. 14

ПРИМЕР Вычислить Точное значение = 2, 3925 Пусть h=1 Метод Трапеций = 0, 06767+0, 60653+1+0, 60653+0, 06767 = 2, 3484 15

Метод Симпсона = 0, 33333*(0, 13534+4*0, 60653+2*1+4*0, 60653+0, 13534) = 2, 3743 Точное 2, 3925 Метод Трапеций 2, 3484 Метод Симпсона 2, 3743 16

Пример Вычислить интеграл по формуле Симпсона; объяснить (геометрически) полученный результат с точки зрения близости значения. 17

Примеры заданий 18