Вычисление неизвестных аналитических зависимостей Лямин Андрей Владимирович 1

Вычисление неизвестных аналитических зависимостей Лямин Андрей Владимирович 1

Постановка задачи u f( • ) y Дано: • u={u 0, u 1, … , un} • y={y 0, y 1, … , yn} Найти: • y = f (u) 2

Методы вычисления • Интерполяция • Аппроксимация 3

Интерполяция функций Интерполяционная формула сопоставляет с функцией функцию известного класса , зависящую от параметров , выбранных так, чтобы значения совпадали со значениями для данного множества значений аргумента (узлов интерполяции): . 4

Интерполяционная функция Лагранжа 5

Пример 1: Пусть: • u={0, 1, 2, 3} • y={0, 1, -1, 0} Тогда: 6

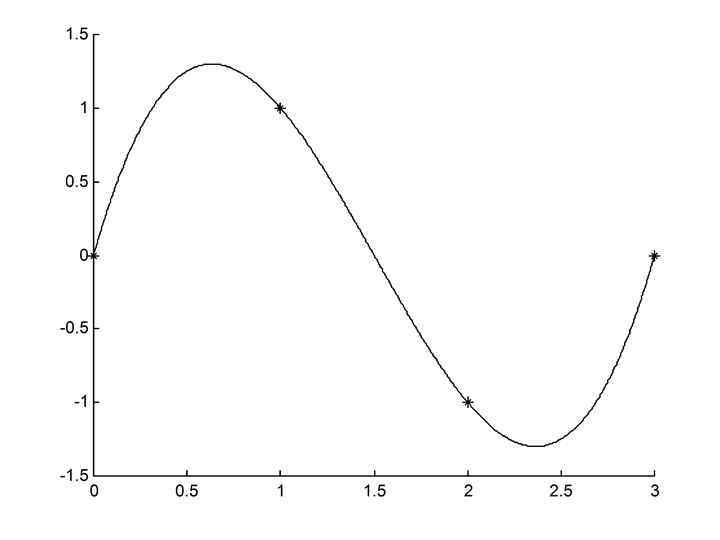7

Интерполяционная функция Ньютона 8

Пример 2: Пусть: • u={0, 1, 2, 3} • y={0, 1, -1, 0} Тогда: 9

10

Аппроксимация функциональных зависимостей 11

Решение задачи аппроксимации 12

Пример 3: Пусть: • u={0, 1, 2, 3}, y={0, 1, 0, 1}, =[1, u]T Тогда: 13

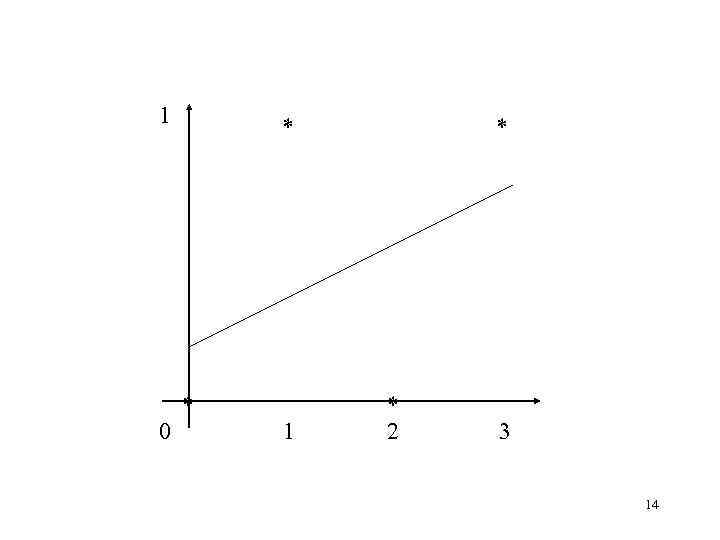1 0 * * 1 * * 2 3 14

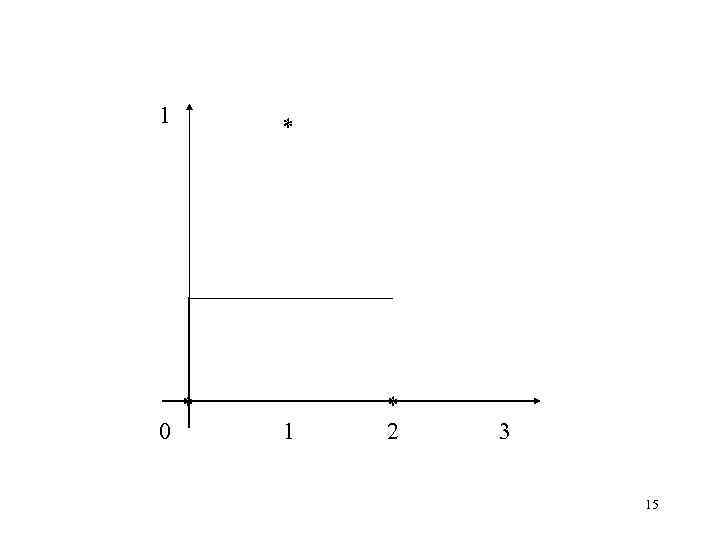1 0 * * 1 * 2 3 15

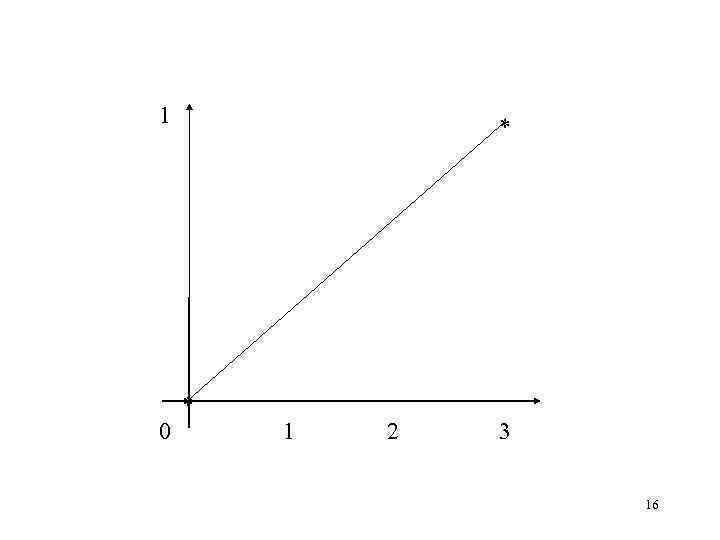1 0 * * 1 2 3 16

Способы повышения точности аппроксимации • Замена базисных функций • Увеличение количества базисных функций 17