Выборочное наблюдение ВН Понятие и виды ВН

Выборочное наблюдение (ВН)

Понятие и виды ВН l ВН – вид несплошного наблюдения, которое обеспечивает отбор в случайном порядке части единиц совокупности и возможность последующего распространения полученных данных на всю совокупность единиц.

Обусловленность ВН l l Выборочное наблюдение применяется, когда применение сплошного наблюдения физически невозможно из-за большого массива данных или экономически нецелесообразно. Физическая невозможность имеет место, например, при изучении пассажиропотоков, рыночных цен, семейных бюджетов. Экономическая нецелесообразность имеет место при оценке качества товаров, связанной с их уничтожением, например, дегустация, испытание кирпичей на прочность и т. п.

Понятие о генеральной и выборочной совокупности l l Генеральная совокупность — это совокупность, из которой производится отбор. Все обобщающие показатели данной совокупности называются генеральными. Выборочная совокупность (выборка) — это совокупность отобранных единиц. Все ее обобщающие показатели называются выборочными.

При этом число единиц в выборке обозначают n, а в генеральной совокупности - N. l l Отношение n/N называется относительный размер или доля выборки. l

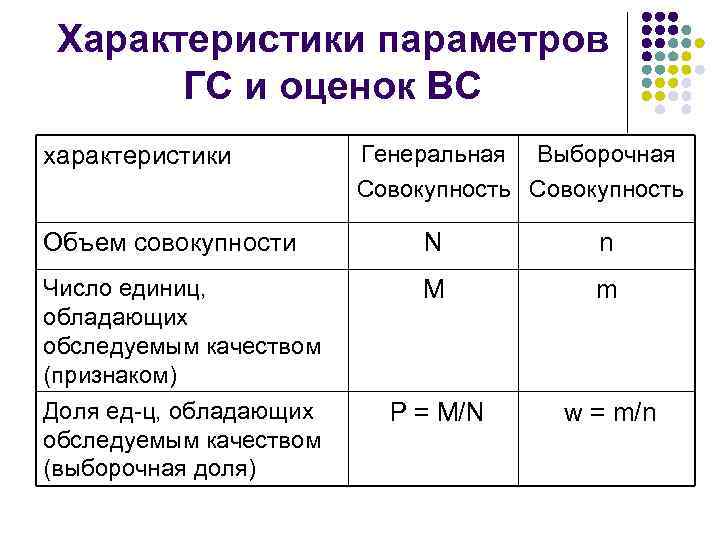
Характеристики параметров ГС и оценок ВС характеристики Генеральная Выборочная Совокупность Объем совокупности N n Число единиц, обладающих обследуемым качеством (признаком) Доля ед-ц, обладающих обследуемым качеством (выборочная доля) M m P = M/N w = m/n

Характеристики параметров ГС и оценок ВС характеристики Генеральная Совокупность Выборочная Совокупность Среднее значение признака x = ∑ x/ N x = ∑ x / n Дисперсия количественного признака ∑ (xi – x ср)2 σ2 x= ------ N σ2 p= pq ∑ (xi – x выб)2 σ2 x= ------ n σ2 w= w(1 -w) Дисперсия альтернативного признака (доли)

Понятие о репрезентативности l l Качество результатов выборочного наблюдения зависит от репрезентативности выборки, то есть от того, насколько она представительна в ГС. Для обеспечения репрезентативности выборки необходимо соблюдать принцип случайности отбора единиц, который предполагает, что на включение единицы ГС в выборку не может повлиять какой-либо иной фактор, кроме случая.

ВИДЫ ВЫБОРКИ ПО СПОСОБУ ОРГАНИЗАЦИИ l l l СОБСТВЕННО СЛУЧАЙНАЯ ТИПИЧЕСКАЯ (РАССЛОЕННАЯ, СТРАТИФИЦИРОВАННАЯ, РАЙОНИРОВАННАЯ) СЕРИЙНАЯ (ГНЕЗДОВАЯ) МНОГОСТУПЕНЧАТАЯ МНОГОФАЗОВАЯ

Способы случайного отбора l l Собственно случайный отбор или «метод лото» , когда статистическим величинам присваиваются порядковые номера, заносимые на определенные предметы (например, бочонки), которые затем перемешиваются в некоторой емкости (например, в мешке) и выбираются наугад. На практике этот способ осуществляют с помощью генератора случайных чисел или математических таблиц случайных чисел. СОБСТВЕННО СЛУЧАЙНАЯ ВЫБОРКА

Способы случайного отбора по определенной схеме l l l Механический отбор, согласно которому отбирается каждая (N/n)-я величина генеральной совокупности. Например, если она содержит 100 000 величин, а требуется выбрать 1 000, то в выборку попадет каждая 100 000 / 1000 = 100 -я величина. Причем, если они не ранжированы, то первая выбирается наугад из первой сотни, а номера других будут на сотню больше. Например, если первой оказалась единица № 19, то следующей должна быть № 119, затем № 219, затем № 319 и т. д. Если единицы генеральной совокупности ранжированы, то первой выбирается № 50, затем № 150, затем № 250 и так далее. ВЫБОРКА ПО СХЕМЕ

Способы случайного отбора по определенной схеме l l Отбор величин из неоднородного массива данных ведется стратифицированным (расслоен ным) способом, когда генеральная совокупность предварительно разбивается на однородные группы, к которым применяется случайный или механический отбор. СТРАТИФИЦИРОВАННАЯ ВЫБОРКА

Способы случайного отбора по определенной схеме l l l Особый способ составления выборки представляет собой серийный отбор, при котором случайно или механически выбирают не отдельные величины, а их серии (последовательности с какогото номера по какой-то подряд), внутри которых ведут сплошное наблюдение. СЕРИЙНАЯ (гнездовая) ВЫБОРКА

Многоступенчатая выборка l l l Несколько стадий отбора, каждой стадиисвоя единица наблюдения Число стадий = числу типов единиц отбора Двухступенчатое иссл бюджетов ДХ: Гор и сельские участки переписи ДХ домашние хозяйства

Многофазовая выборка l l l Несколько стадий отбора, но единая единица отбора Каждая ступень отбора имеет свой объем ВН и свою программу наблюдения Перепись населения

Способы отбора l l Повторный отбор (схема возвращенного шара) - характеризуется тем, что численность единиц генеральной совокупности в процессе выборки остается постоянной. Определенную единицу, попавшую в выборку, после регистрации опять возвращают в генеральную совокупность, и она сохраняет равную возможность со всеми прочими единицами при повторном отборе единиц снова попасть в выборку Вероятность попадания любой единицы в выборку равна 1/N, и она остается постоянной на протяжении всей процедуры отбора.

Способы отбора l l Бесповторный отбор (схема невозвращенного шара). При такой выборке единица совокупности, попавшая в выборку, в генеральную совокупность не возвращается и в дальнейшем в выборке уже не участвует. При бесповторной выборке численность единиц генеральной совокупности сокращается в процессе исследования. Вероятность попадания в выборку изменяется от 1/N для первой отбираемой единицы, до 1/(N - n -1) для последней.

Преимущества выборочного метода над сплошным l l Достижение большой точности результатов исследования благодаря сокращению ошибок, происходящих при регистрации. При обращении к выборкам обеспечивается экономия материальных, трудовых, финансовых ресурсов и времени в результате сокращения объема работы. Сведение к минимуму порчи или уничтожения анализируемых объектов. Необходимость детального исследования каждой единицы наблюдения при невозможности охвата всех единиц.

Основные этапы проведения выборочного наблюдения l l l Определение нужного объема выборки и способа отбора. Проведение отбора. Обобщение данных и расчет выборочных характеристик. Расчет ошибок выборки Распространение выборочных характеристик на генеральную совокупность.

2. Ошибки выборки l l Расхождение между значениями показателей ГС и ВС называют ошибками репрезентативности. Случайные и систематические Случайные – неравномерное представление в ВС различных категорий единиц ГС Систематические – с нарушением правил отбора или условий реализации выборки.

Величина случайной ошибки l l l 1. от объема ВС 2. степени вариации изучаемого признака в генеральной совокупности 3. принятого способа формирования ВС Различают: Среднюю (стандартную) – μ ( «мю» ) Предельную – Δ ( «дельта» )

l l Средняя ошибка характеризует меру отклонения Выборочных показателей от показателей ГС. Предельная ошибка –максимально возможное расхождение ВС и ГС, т. е. максимум ошибки при заданной вероятности ее появления.

Ошибки выборочной средней и выборочной доли l l μ выборочной средней и μ выборочной доли Δ выборочной средней Δ выборочной доли

Формулы расчета средней ошибки μ для простой собственно случайной выборки Способ отбора Повторный Бесповторный Для выборочной средней доли

Пример l l l В областном центре было опрошено 1000 студентов техникумов, с целью выяснить, как часто они посещают кинотеатры. По результатам 5%-ой выборки установлено, что в среднем студент посещает кинотеатр 5 раз в месяц при среднеквадратическом отклонении 2 раза в месяц. Определим насколько результаты, полученные при опросе студентов, отличаются от генеральной совокупности студентов города.

Пример расчета средней ошибки выборочной средней l Для ответа на поставленный вопрос, надо найти среднюю ошибку выборки. По условию задачи: произведена 5%- ная выборка, т. е. = 0, 05; среднеквадратическое отклонение равно 2 раза в месяц, т. е. S = 2, так как 2 = S 2, то 2= 22 = 4; было опрошено 1000 студентов, т. е. n = 1000. l 0, 06 раз в месяц. l l

Пример расчета средней ошибки выборочной доли l l l При опросе студентов техникумов, выяснилось, что 358 студентов не менее 3 раз в месяц смотрели мультфильмы в кинотеатрах города. Определим насколько полученные результаты, будут отличаться от генеральной совокупности. Решение: Для этого найдем среднюю ошибку доли студентов, смотрящих мультфильмы не менее 3 раз в месяц: определим долю студентов: m = 358 разделим на n = 1000, w = 0, 358, или 35, 8% Далее найдем μw = 0, 015, или 1, 5% составляет средняя ошибка доли студентов, которые смотрят мультфильмы не менее 3 раз в месяц.

Формула расчета предельной ошибки ВН l При любом способе отбора с определенной вероятностью можно утверждать, что отклонение выборочной средней (доли) не превысит некоторую величину, принятую называть предельной ошибкой выборки. l Δ = μ * t, где t – коэф. доверия, определяемый в зависимости от уровня вероятности F(t).

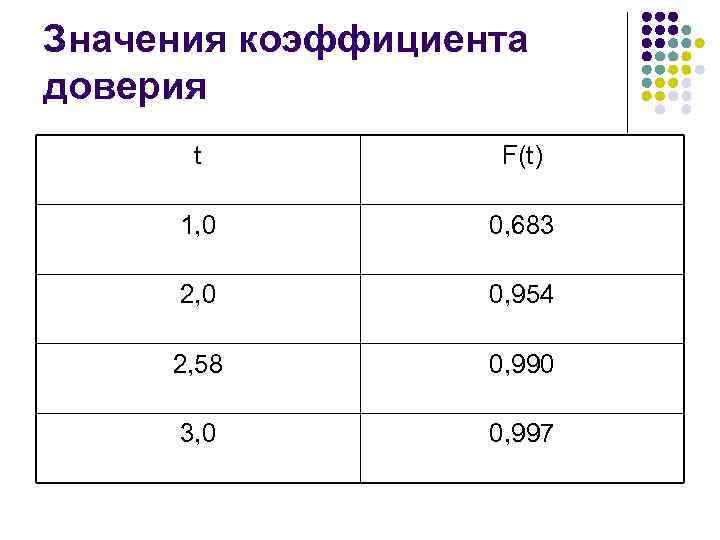
Значения коэффициента доверия t F(t) 1, 0 0, 683 2, 0 0, 954 2, 58 0, 990 3, 0 0, 997

Смысл коэффициента доверия l l При t = 2 вероятность F(t) = 0, 954 – из каждой 1000 единиц выборочной совокупности 954 дадут обобщающие показатели, которые будут отличаться от генеральных не более чем на двукратную среднюю ошибку выборки

Пределы генеральных параметров l Расчет средней и предельной ошибок позволяет определить пределы, в которых будут находиться характеристики ГС: l l x – Δ x≤ X ≤ x + Δx w – Δ w≤ P ≤ w + Δw

Пример расчета предельной ошибки выборочных средней и доли l l l С вероятностью 0, 954 определим пределы, в которых находятся число посещений кинотеатров студентами за месяц и доля студентов смотрящих мультфильмы не менее 3 раз в месяц. Решение: Доверительной вероятности 0, 954 соответствует значение коэффициента доверия t =2, 0. Тогда предельная ошибка выборки при определении среднего числа посещений кинотеатра студентами составит: Δ = 0, 06 * 2 = 0, 012 Следовательно, среднее число посещений кинотеатра студентами техникумов города находится в пределах: 5 - 0, 12 X 5 + 0, 12 или 4, 88 X 5, 12 С вероятностью 0, 954 можно утверждать, что среднее число посещений кинотеатров студентами составляет от 4, 88 до 5, 12 раз в месяц.

Пример расчета предельной ошибки выборочных средней и доли l Предельная ошибка доли: Δ = t*μ =2 *0, 015 = 0, 03 l Таким образом, доля студентов смотрящих мультфильмы в кинотеатрах города более трех раз в месяц в генеральной совокупности находится: l 35, 8% - 3, 0% P 35, 8% + 3, 0% l или 32, 8% P 38, 8%. l С вероятностью 0, 954 можно гарантировать, что доля студентов техникумов города, которые смотрят мультфильмы более 3 раз в месяц, составляет не менее 32, 8% и не более 38, 8% от общего числа студентов.

3. Задачи, решаемые применении ВН l l l Определение необходимой численности выборки - n Определение степени доверия выборочным данным - t Распространение данных выборочного наблюдения на генеральную совокупность

Определение необходимой численности выборки - n l Формулы для определения необходимой численности выборки (n – объем выборки) можно получить из формул определения ошибок выборки. На практике объем выборки рассчитывают вначале по формуле для повторного отбора: l Если полученное значение nовт. превышает 5% численности генеральной совокупности, то расчет проводят по формуле для бесповторного отбора: l l Если численность выборки не превышает 5% генеральной совокупности, то к формуле для бесповторного не переходят

Пример l l Для изучения товарооборота по продаже канцелярских товаров планируется провести выборочное обследование торговых предприятий области. Сколько предприятий розничной торговли из 5000 действующих в области надо обследовать, если по данным предыдущего обследования известно, что коэффициент вариации товарооборота по данной группе товаров составляет 45%, а предельная относительная ошибка выборки с вероятностью 0, 997 не должна превысить 6%?

Распространение данных ВН на ГС l l l 1. Способ прямого пересчета используется в том случае, если цель выборочного наблюдения — определение объема генеральной совокупности, когда известна лишь численность ее единиц. Согласно данного способа выборочную среднюю или долю умножают на численность единиц генеральной совокупности и получают соответствующий объемный показатель. В таком случае нужно указывать доверительные интервалы: нижняя граница — обобщающая характеристика выборочной совокупности за вычетом предельной ошибки, верхняя граница — обобщающая характеристика плюс предельная ошибка.

Распространение данных ВН на ГС l Способ поправочных коэффициентов используется тогда, когда выборочное наблюдение проводится с целью уточнения результатов сплошного наблюдения. Система проведения такого способа следующая: После исследования сплошного наблюдения проводят выборочное наблюдение и устанавливают «процент недоучета» при сплошном наблюдении. Этот процент и будет тем поправочным коэффициентом, который нужно распространить на всю генеральную совокупность.