Выборочное наблюдение Генеральная совокупность это

Выборочное наблюдение

Генеральная совокупность – это вся изучаемая совокупность единиц, подлежащая изучению по интересующим исследователя признакам. Выборочная совокупность или выборка – это отобранная в случайном порядке из генеральной совокупности некоторая ее часть, позволяющая делать более или менее точные выводы относительно совокупности в целом. Репрезентативность выборки – свойство выборочной совокупности воспроизводить характеристики генеральной совокупности.

Суть выборочного наблюдения сводится к решению трех проблем: Как должен происходить отбор элементов выборки. Каков должен быть объем выборки. В какой мере можно положиться на результаты выборки

Для простой случайной выборки существуют разные принципы отбора Повторный отбор После отбора какой-либо единицы она снова возвращается в совокупность и опять может быть выбранной Бесповторный отбор В этом случае каждая отобранная единица не возвращается обратно.

Способы отбора выборочной совокупности: собственно случайный механический (систематический) типический (стратифицированный, расслоенный) серийный (гнездовой) Комбинированный

Плюсы и минусы простой случайной выборки Плюсом данного способа является полное соблюдение принципа случайности и, как следствие – избежание систематических ошибок. Недостатки: необходимость наличия списка элементов генеральной совокупности сложность проведения опроса сравнительно большого объема выборки

Механическая выборка Для механической выборки необходим список элементов генеральной совокупности (например, фамилии, адреса, номера телефонов и т. п. ). Из этого списка через равные промежутки элементы отбираются в выборку. Этот промежуток называется шагом выборки (отбора). Шаг рассчитывается путем деления числа единиц генеральной совокупности на число единиц в выборочной совокупности. Плюсом является менее громоздкая процедура отбора.

Недостатки не для каждой совокупности можно составить полный список ее элементов можно применять, если единицы генеральной совокупности в основе выборки расположены в случайном порядке проблема недостижимости респондентов – невозможности опросить именно тех людей, которые попали в случайный отбор в связи с их отсутствием или нежеланием участвовать в опросе рассеянное территориально поле респондентов – например, если выборка распределяется по территории страны, то полученные адреса могут находиться далеко друг от друга, и это усложняет проведение полевых работ

Стратифицированная выборка При стратифицированном отборе генеральная совокупность разделяется на однородные группы (страты) по какому-либо признаку. В основу выделения страт закладывается определенный критерий (признак или группа признаков), и страты, объединяя однотипные элементы, различаются между собой по этому критерию. Стратифицированная выборка оказывается точнее собственно-случайной. Этот метод особенно хорош, когда генеральная совокупность неоднородна.

Недостатки может быть применена лишь при наличии дополнительной информации о генеральной совокупности возможность систематической ошибки, например, из-за неточной информации о параметрах генеральной совокупности

Серийная (гнездовая) выборка Единицей отбора при серийной (гнездовой) выборке являются группы (гнезда). Например, населенные пункты, районы, предприятия. Единицы исследования здесь размещены компактно. Группы отбираются случайно. Объекты, отобранные в группу, подлежат сплошному обследованию. Преимущество отбора сериями состоит в том, что достигается значительная экономия затрат на обследование благодаря более компактному размещению обследуемых объектов в пространстве. Это гораздо проще в организационном плане, так как проще выбрать несколько групп и опросить их целиком, чем бегать за каждым респондентом.

Недостатки - необходимо следить, чтобы количество групп в генеральной совокупности было достаточно большим, иначе нарушается принцип случайности - возможны перекосы из-за того, что на момент опроса не удается застать всех членов группы

Ошибка выборки

Ошибки регистрации свойственны любому статистическому наблюдению вообще и появление их может быть вызвано несовершенством измерительных приборов, недостаточной квалификацией наблюдателя, неточностью подсчетов и т. п. Можно полагать, что по сравнению со сплошным наблюдением опасность возникновения ошибок регистрации проведении выборочных наблюдений должна быть меньше, т. к. выборочные наблюдения проводятся по меньшему кругу обследуемых объектов с участием более квалифицированных работников и, следовательно, более тщательно. Значительно уменьшается при выборочном наблюдении и опасность преднамеренных искажений данных, т. к. специально подобранные и обученные наблюдатели в них не заинтересованы.

Ошибки репрезентативности присущи только несплошным наблюдениям и представляют собой расхождение между величиной полученных по выборке показателей и величиной этих показателей, которые были бы получены при проведенном с одинаковой степенью точности сплошном наблюдении.

Систематические ошибки могут возникать в связи с особенностями принятой системы отбора и обработки данных наблюдений или в связи с нарушением установленных правил отбора. Возникновение случайных ошибок репрезентативности объясняется недостаточно равномерным представлением в выборочной совокупности различных категорий единиц генеральной совокупности, в силу чего распределение отобранной совокупности единиц не вполне точно воспроизводит распределение единиц генеральной совокупности.

Величина случайной ошибки репрезентативности зависит: от принятого способа формирования выборочной совокупности, выбор которого связан с решением вопросов о единице отбора, способе отбора единиц, способе размещения всего объёма отбираемых единиц по различным группам генеральной совокупности; объёма выборки от степени колеблемости изучаемого признака в генеральной совокупности.

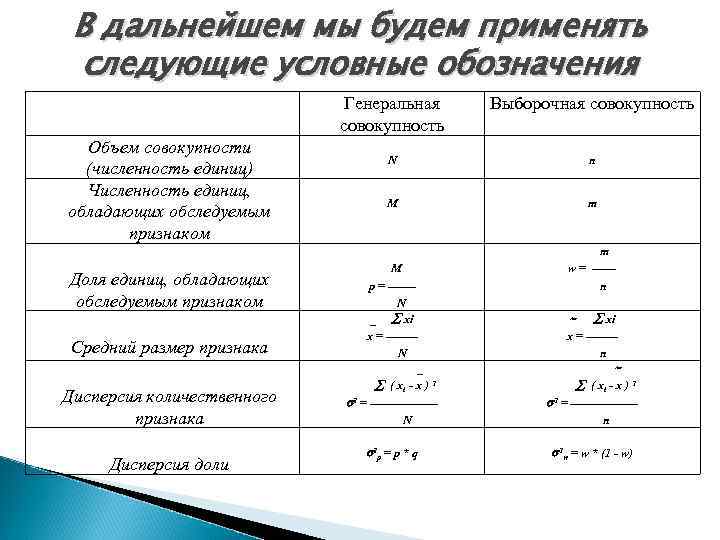
В дальнейшем мы будем применять следующие условные обозначения Генеральная совокупность Объем совокупности (численность единиц) Численность единиц, обладающих обследуемым признаком Выборочная совокупность N n M m Средний размер признака M p = ------N _ xi x = -------N Дисперсия количественного признака _ ( xi - x ) 2 2 = --------N Доля единиц, обладающих обследуемым признаком Дисперсия доли 2 p = p * q m w = -----n xi x = -------n ( xi - x ) 2 2 = --------n 2 w = w * (1 - w)

Средняя и предельная ошибки выборки = t* – предельная ошибка выборки; – средняя ошибка выборки; t – коэффициент доверия, определяемый в зависимости от уровня вероятности p.

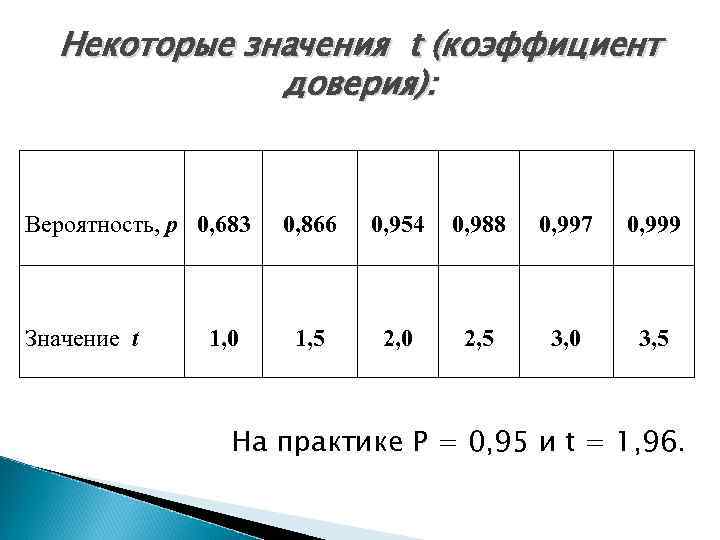
Некоторые значения t (коэффициент доверия): Вероятность, p 0, 683 Значение t 1, 0 0, 866 0, 954 0, 988 0, 997 0, 999 1, 5 2, 0 2, 5 3, 0 3, 5 На практике Р = 0, 95 и t = 1, 96.

Средняя ошибка выборки при случайном повторном отборе = ---- n

Средняя ошибка выборки при случайном бесповторном отборе ______ 2 n = ----- * ( 1 - ---- ) n N 2 – выборочная дисперсия; s– выборочное среднее квадратическое отклонение; n – объем выборочной совокупности; N – объем генеральной совокупности.

Пределы для выборочной средней _ x - x x x + x , _ где x и x - генеральная и выборочная средние соответственно; x - предельная ошибка выборочной средней.

Пример 1. При проверке веса импортируемого груза на таможне методом случайной повторной выборки было отобрано 200 изделий. В результате был установлен средний вес изделия 30 г при среднем квадратическом отклонении 4 г. С вероятностью 0, 997 определите пределы, в которых находится средний вес изделия в генеральной совокупности. Решение. Рассчитаем предельную ошибку выборки. Так как при p = 0, 997 t = 3, предельная ошибка равна: x 4 x = t * ------ = 3 * ----- = 0, 84. n 200 Определим пределы генеральной средней: _ 30 - 0, 84 x 30 + 0, 84 или: _ 29, 16 x 30, 84. Следовательно, с вероятностью 0, 997 можно утверждать, что средний вес изделий в генеральной совокупности находится в пределах от 29, 16 г до 30, 84 г.

Пример 2. С целью определения средней фактической продолжительности рабочего дня в учреждении с численностью работающих 480 человек было проведено 25%-е случайное бесповторное выборочное обследование. По его результатам выяснилось, что у 10% обследованных потери рабочего времени достигали более 45 мин. в день. С вероятностью 0, 683 установите пределы, в которых находится генеральная доля работников с потерями рабочего времени более 45 мин. в день.

Решение. Определим объем выборочной совокупности: n = 480 * 0, 25 = 120 чел. Выборочная доля w равна по условию 10%. Учитывая, что при p = 0, 683 t = 1, вычислим предельную ошибку выборочной доли: _________ w * (1 - w) n 0, 1*(1 -0, 1) 120 w = ------- * (1 - ----) =1* -------- * (1 - ------) = 0, 0237 2, 4%. n N 120 480 Пределы доли признака в генеральной совокупности: 10 - 2, 4 p 10 + 2, 4 или 7, 6 p 12, 4. Таким образом, с вероятностью 0, 683 можно утверждать, что доля работников учреждения с потерями рабочего времени более 45 мин. в день находится в пределах от 7, 6 % до 12, 4%.

При типической (стратифицированной) выборке отбор единиц может быть организован либо пропорционально объему типических групп, либо пропорционально внутригрупповой дифференциации признака. При выборке, пропорциональной объему типических групп, число единиц, подлежащих отбору из каждой группы, определяется следующим образом: Ni ni = n* ---- , N Ni -- объем i-й группы; ni -- объем выборки из i-й группы.

Средняя ошибка при типической выборки ______ __ 2 i = ------ n (повторный отбор) ; _________ __ 2 i n = ------- * ( 1 - ---- ) n N __ (бесповторный отбор) , где 2 i – средняя из внутригрупповых дисперсий.

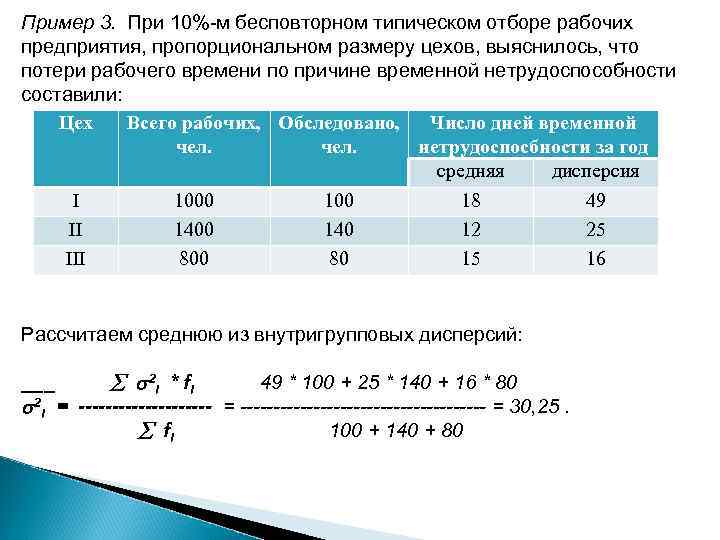
Пример 3. При 10%-м бесповторном типическом отборе рабочих предприятия, пропорциональном размеру цехов, выяснилось, что потери рабочего времени по причине временной нетрудоспособности составили: Цех Всего рабочих, Обследовано, Число дней временной чел. нетрудоспосбности за год средняя дисперсия I 1000 18 49 II 1400 140 12 25 III 800 80 15 16 Рассчитаем среднюю из внутригрупповых дисперсий: ___ 2 i * fi 49 * 100 + 25 * 140 + 16 * 80 2 i = ----------------------------- = 30, 25. fi 100 + 140 + 80

Определим среднюю и предельную ошибки выборки (с вероятностью 0, 954): __________ 30, 25 320 = ---- * ( 1 - ---- ) = 0, 29 ; x = 2 * 0, 29 = 0, 58. 3200 Рассчитаем выборочную среднюю: xi * ni 18 * 100 + 12 * 140 + 15 * 80 x = ---------------------------- = 14, 6 дня. ni 100 + 140 + 80 С вероятностью 0, 954 можно сделать вывод, что среднее число дней временной нетрудоспособности одного рабочего в целом по предприятию находится в пределах _ 14, 6 - 0, 58 х 14, 6 + 0, 58.

Средняя ошибка при серийной (гнездовой) выборке _____ 2 = ------- (повторный отбор) ; r ________ 2 r = ------ * ( 1 - ---- ) r R (бесповторный отбор) , где r – число отобранных серий; R – общее число серий.

Межгрупповую дисперсию вычисляют следующим образом: ( xi - xо ) 2 2 = ---------- , r где xi – средняя i-й серии; xо – общая средняя по всей выборочной совокупности.

Пример 4. На опытном поле площадью 20 га проводилось выборочное обследование урожайности сельхозкультур. Были обследованы пять делянок площадью по 1 га. Средние урожайности на них составили соответственно 14, 5 ц/га, 16 ц/га, 15, 5 ц/га, 15 ц/га и 14 ц/га. С вероятностью 0, 954 определите пределы урожайности во всей области. Решение. Рассчитаем общую среднюю: 14, 5 + 16 + 15, 5 + 14 х = -------------------- = 15 ц/га. 5

Межгрупповая (межсерийная) дисперсия равна: (14, 5 - 15)2 + (16 - 15) 2 + (15, 5 - 15) 2 + (14 - 15) 2 2 = ---------------------------------------- = 0, 5. 5 Определим предельную ошибку серийной (бесповторной) выборки (t = 2 при p = 0, 954): _________ 0, 5 5 x = 2 * ------- * ( 1 - ------ ) 1, 7. 5 20 Следовательно, урожайность на опытном поле будет с вероятностью 0, 954 находиться в пределах: _ 15 - 1, 7 х 15 + 1, 7 или _ 13, 3 ц/га х 16, 7 ц/га.

Объем выборки

Объем выборки – это общее число единиц наблюдения, включенных в выборочную совокупность. Объем выборки зависит от степени однородности генеральной совокупности и от необходимой степени точности выборочных результатов. Объем выборки рассчитывается по формулам, дифференцированным в зависимости от вида выборки В качестве исходных данных используется информация о допустимом пределе ошибки выборки, о доверительной вероятности, об объеме генеральной совокупности, о дисперсии, оценивающей степень неоднородности генеральной совокупности.

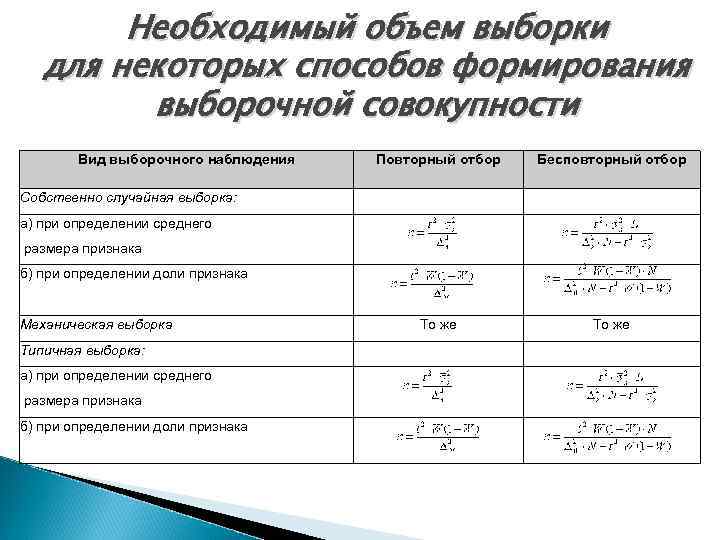
Необходимый объем выборки для некоторых способов формирования выборочной совокупности Вид выборочного наблюдения Повторный отбор Бесповторный отбор Собственно случайная выборка: а) при определении среднего размера признака б) при определении доли признака Механическая выборка То же Типичная выборка: а) при определении среднего размера признака б) при определении доли признака

Пример расчета объема выборки В микрорайоне проживает 5000 семей. В порядке случайной бесповторной выборки предполагается определить средний размер семьи при условии, что ошибка выборочной средней не должна превышать 0, 8 человека с вероятностью Р=0, 954 и при среднем квадратичном отклонение определены на основе пробного обследования. Формула расчета величины выборочной совокупности, осуществляемой одноступенчатым случайным бесповторным отбором, имеет следующий вид: где n - объем выборочной совокупности; N - объем генеральной совокупности; t - коэффициент доверия σ2 – среднее квадратическое отклонение. Так как при Р = 0, 954 t = 2, то в этом случае численность выборки равна: