Вводная лекция КВАНТОВЫЕ СВОЙСТВА МИКРОЧАСТИЦ Кванты электромагнитного

Вводная лекция КВАНТОВЫЕ СВОЙСТВА МИКРОЧАСТИЦ

Кванты электромагнитного излучения • 1900 г. Планк создает квантовую теорию излучения света. Свет (электромагнитное излучение) испускается в виде порций (квантов), энергия кванта где излучения. – постоянная Планка; n – частота • 1905 г. Эйнштейн разрабатывает квантовую теорию фотоэффекта. Электроны тела поглощают свет квантами. Формула Эйнштейна для фотоэффекта • Вывод: свет (электромагнитное излучение) существует в виде неделимых порций – квантов.

Дуализм света • Волновая теория представляет свет в виде электромагнитных волн. Уравнение поляризованной волны, распространяющейся вдоль х: Волновые свойства света подтверждаются явлениями интерференции, дифракции, поляризации. • Квантовая теория представляет свет в виде неделимых порций – квантов, т. е. свет обладает корпускулярными свойствами. Квантовые свойства света (электромагнитного излучения) подтверждаются законами теплового излучения, фотоэффекта, излучения атомов и молекул. По предложению Эйнштейна кванты света называют фотонами (название «корпускул» света по Ньютону). • Корпускулярно-волновой дуализм света: свет в одних случаях ведет себя как частица, в других случаях – как волна.

Свойства фотонов • Энергия фотона. • Импульс фотона р находится через энергию. Для ультрарелятивистских частиц E = pc, где с – скорость света в пустоте. Откуда получим формулы для расчета импульса фотона: • Фотон обладает моментом импульса L: • Квантовая теория не отвергает волновые свойства фотонов. Энергия и импульс фотонов определяется с помощью частоты (длины волны) света, т. е. фотоны – это частицы, проявляющие волновые свойства.

Волновые свойства электронов • 1924 г. де Бройль предложил гипотезу о корпускулярноволновом дуализме микрочастиц. Согласно де Бройлю, длина волны электрона определяется формулой (1) где h – постоянная Планка; р – импульс частицы. • 1927 г. Дэвиссон и Джермер исследовали отражение электронов от монокристалла Ni. Отраженные электроны собирались с помощью небольшого электрода, который можно было ориентировать под разными углами q относительно поверхности кристалла. Ученые обнаружили, что сила тока в гальванометре изменялась от угла q также, как при дифракции волн.

Схема опыта Дэвиссона и Джермера j К – монокристалл никеля; А – источник электронов; В – приемник электронов; S – шлифованная плоскость кристалла; q – угол дифракции электронов. Электронный луч падает по нормали к плоскости S; кристалл вращают относительно оси О. В данном опыте кристалл является дифракционной решеткой для волн де Бройля.

Величина тока гальванометра I(j)

Электронограмма 1927 г. Дж. П. Томсон исследует прохождение электронного пучка через тонкую фольгу золота

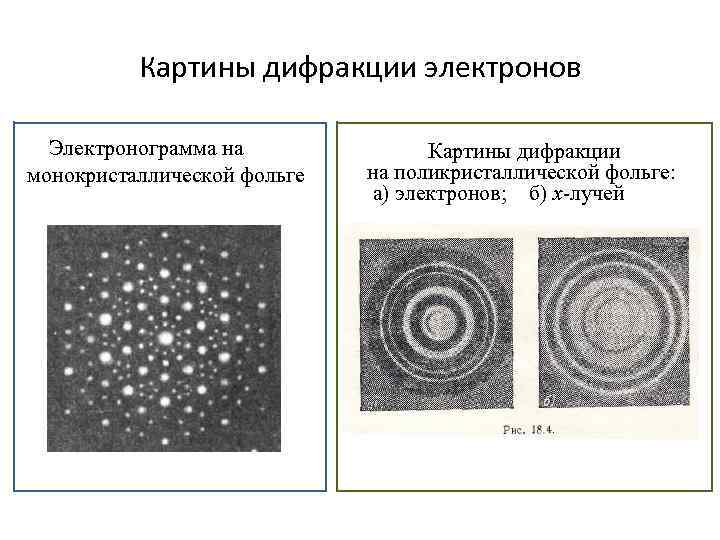Картины дифракции электронов Электронограмма на монокристаллической фольге Картины дифракции на поликристаллической фольге: а) электронов; б) х-лучей

Соотношение неопределенностей для пакета волн Из теории волн: где s – возмущение среды; А – амплитуда колебаний; w – циклическая частота; – волновое число; l – длина волны; х – координата (расстояние от источника). Для неограниченной волны (x , k = const); для пакета (цуга) волн где Dx – длина пакета (неопределенность координаты); Dk – неопределенность волнового числа. Пакет волн можно представить в виде суперпозиции волн разной длины:

Соотношение неопределенностей Гейзенберга для микрочастиц Для электронных волн де Бройля (2) Соотношение неопределенностей Гейзенберга для электронной волны, распространяющейся вдоль оси х: (3) Из соотношения неопределенностей следует, что нельзя одновременно точно знать координату частицы и ее импульс. Чем точнее будем определять положение частицы, тем хуже будет определен ее импульс. Из соотношения неопределенностей (4) найдем неопределенность скорости: Вывод: для микрочастиц невозможно одновременно точно знать координату частицы и ее скорость; понятие траектории в квантовой теории теряет физический смысл.

Иллюстрации к соотношению неопределенностей 1) 2) 3)

Классическое и квантовое описание движения электрона Пусть энергия электрона равна E = 10 э. В = Импульс электрона Пример 1 Электрон движется в электронной лампе с межэлектродным расстоянием Dx = 1 см. Поскольку Dx >> l, классическое описание вполне допустимо. Пример 2 Электрон движется в твердом теле, расстояние между атомными плоскостями Поскольку Dx ~ l, необходимо квантовое описание движения.

Уравнение Шредингера для стационарных состояний (E = const) Уравнение Шредингера (5) является основным уравнением квантовой механики; где: Статистический смысл волновой функции: произведение f(r) = Y(r)Y*(r) определяет вероятность нахождения микрочастицы в данной точке пространства. Формула (6) определяет вероятность нахождения частицы в объеме DV.

Частица, движущаяся вдоль оси х при отсутствии потенциального поля Уравнение Шредингера для рассматриваемого случая Решение уравнения: (6) В комплексной форме Уравнение волны де Бройля: Плоская волна, заполняющая пространство. Импульс частицы: (7) Формула связи импульса и энергии совпадает с классической.

Частица в одномерной потенциальной яме Пусть ширина ямы l, потенциальная энергия частицы внутри ямы , на стенках ямы она скачком изменяется до бесконечности Уравнение Шредингера для частицы в яме Решение уравнения ищем в виде гармонической функции (8) Согласно первому граничному условию (х = 0) Из второго граничного условия (x = l) (9)

Волновая функция электрона в потенциальной яме С учетом граничных условий получим (10) Амплитуду волновой функции найдем из условия нормировки (т. к. полная вероятность обнаружить частицу в яме равна 1). В рассматриваемом случае Y(x) является действительной функцией, поэтому. Откуда В итоге найдем амплитуду и вид волновой функции: (11)

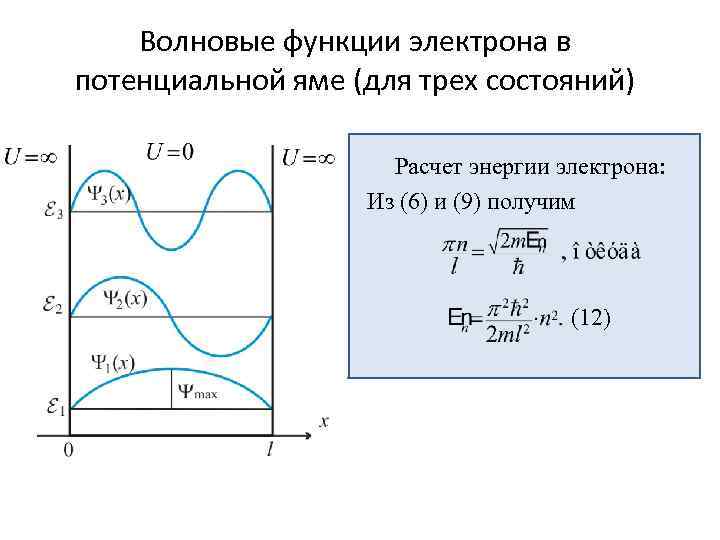Волновые функции электрона в потенциальной яме (для трех состояний) Расчет энергии электрона: Из (6) и (9) получим (12)

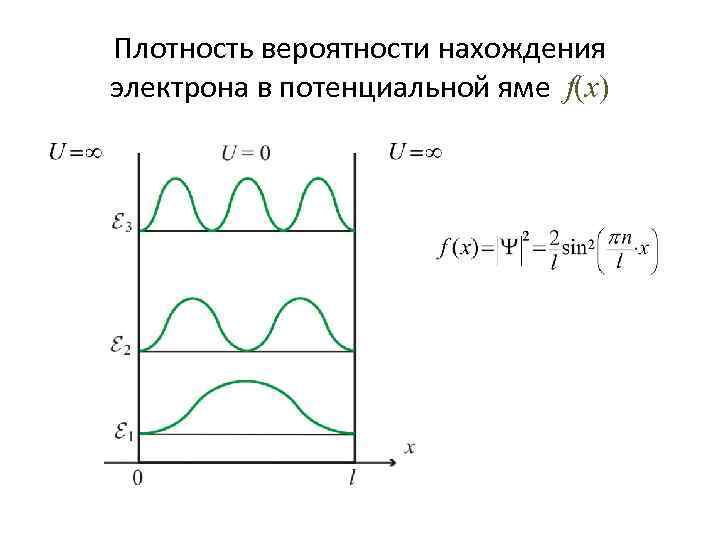Плотность вероятности нахождения электрона в потенциальной яме f(x)

Туннельное прохождение микрочастицы через прямоугольный потенциальный барьер

Пример Пусть энергия электрона E = 0, 71 э. В; высота барьера U = 0, 81 э. В; ширина барьера l = 1 нм. Определить: 1) прозрачность барьера; 2) ток через барьер, если на него падают электронов в секунду; 3) Как изменится D при увеличении ширины барьера в два раза?

Прохождение микрочастицы через непрямоугольный потенциальный барьер

Литература 1. Савельев И. В. Курс общей физики. В 5 кн. Кн. 5. Квантовая оптика. Атомная физика. Физика твердого тела. Физика атомного ядра и элементарных частиц: учеб. пособие для вузов. – М. : Астрель, 2002. С. 69– 100. 2. Иродов И. Е. Квантовая физика; основные законы: учеб. пособие для вузов. – М. : лаборатория базовых знаний, 2001. С. 60– 110. 3. Сивухин Д. В. Общий курс физики. В 6 т. Т. 5. Атомная физика: учеб. пособие для вузов. – М. : наука, 1987. С. 7– 25, 94– 152.