3931deb264c042a484f3ce29ae1e5c3d.ppt
- Количество слайдов: 89


ВВОД ДАННЫХ, ЦИФРОВАНИЕ ИСХОДНОЙ ИНФОРМАЦИИ Есть много способов ввода данных. Одни выглядят примитивными, вроде помещения прозрачной сетки на карту. Другие более современны, так, например, используют устройства цифрового ввода дигитайзеры и сканеры.

Перед тем, как использовать структуры данных, модели и системы, необходимо преобразовать нашу реальность в форму, понимаемую компьютером.

Методы, при помощи которых это будет сделано, зависят в некоторой степени от имеющегося оборудования и от конкретной системы.

1. подсистема ввода спроектирована для переноса графических и атрибутивных данных в компьютер. 2. она должна отвечать хотя бы одному из двух фундаментальных методов представления графических объектов растровому или векторному. 3. она должна иметь связь с системой хранения и редактирования, чтобы гарантировать сохранение и возможность выборки того, что мы введем, и давать возможность устранять ошибки и вносить изменения по мере необходимости.

Вначале необходимо определить, какой тип ГИС, векторный или растровый, будет использоваться, а также будет ли ваша ГИС способна преобразовывать эти типы данных один в другой.

Хотя преобразование между векторной и растровой формами — дело достаточно обычное, есть несколько вещей, о которых следует помнить

Часто при преобразовании векторов в растр результаты получаются визуально удовлетворительными, но методы растеризации могут давать результаты, которые не подходят для атрибутов, представляющих каждую ячейку. Это особенно верно вдоль границ областей, где имеется неопределенность с присвоением ячейкам растра атрибутов с одной или другой стороны границы.

С другой стороны, преобразуя растр в вектор, можно сохранить подавляющее большинство атрибутивных данных, но визуальные результаты будут часто отражать блочный, лестничный вид ячеек растра, из которых преобразование было произведено. Существуют алгоритмы сглаживания этого лестничного эффекта, использующие математические методы сплайн интерполяции.

Информация о качестве данных • • • Дата получения Точность позиционирования Точность классификации Полнота Метод, использованный для получения и кодирования данных

Типы систем ввода данных • 1. ввод с помощью клавиатуры – Гл. обр. для атрибутивных данных – Редко используется для пространственных данных – М. б. совмещен с ручным цифрованием – Обычно более эффективно используется как отдельная операция

• 2. Координатная геометрия – Процедуры, используемые для ввода данных по земельным наделам, кадастр – Очень высокий уровень точности, полученной за счет полевых геодезических измерений – Очень дорогой

• 3. Ручное цифрование – Наиболее широко используемый метод ввода пространственных данных с карт – Эффективность зависит от качества программного обеспечения цифрования и умения оператора – Требует много времени – Допускает наличие ошибок

• 4. Сканирование – Минимальный фрагмент карты – 0. 02 мм – Снимок нуждается в обработке и редактировании для улучшения качества – Изображение должно преобразовываться в векторный формат

• 5. Ввод существующих цифровых файлов – Наборы данных различный организаций и ведомств должны быть доступны – Приобретение и использование существующих цифровых наборов данных является наиболее эффективным способом заполнения ГИС.

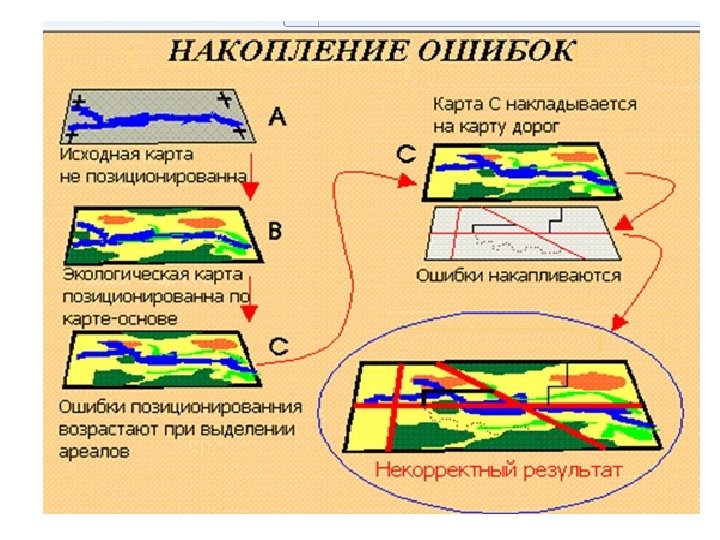
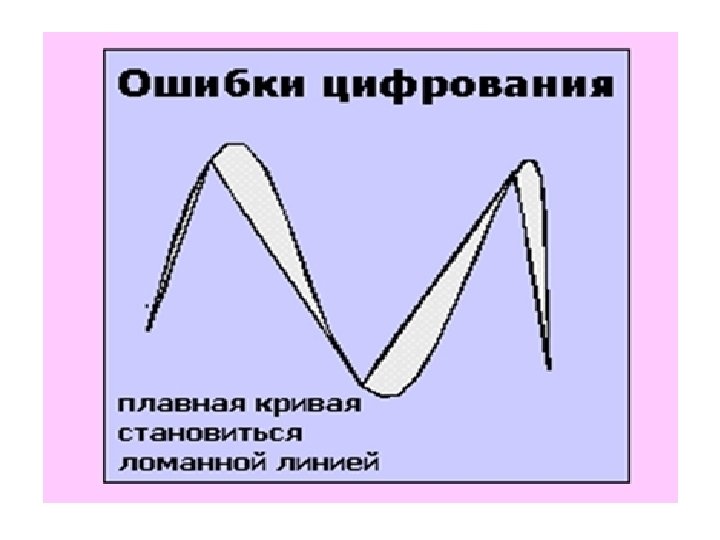
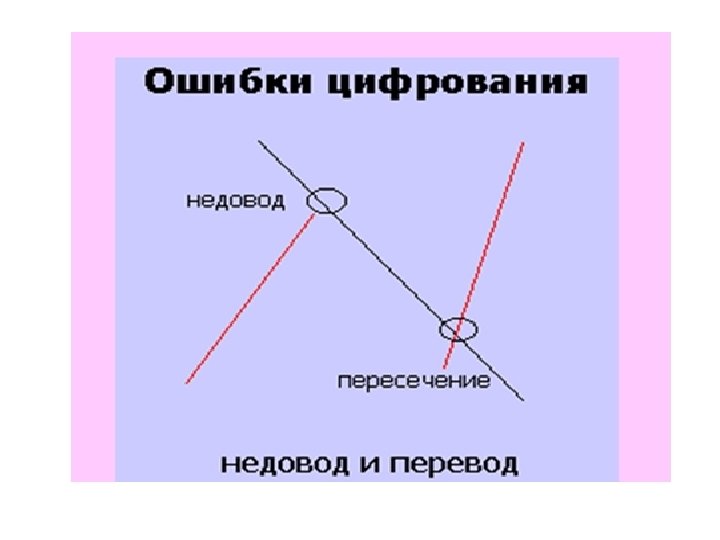
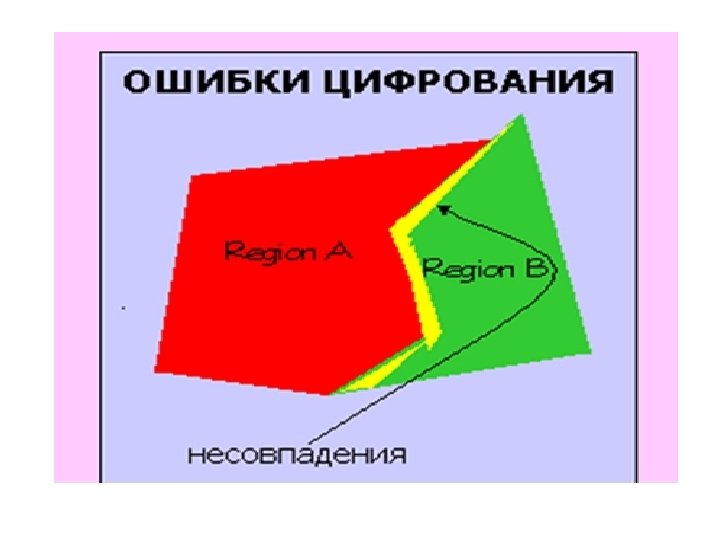
Проблемы цифрования карт • Уровень ошибок в БД ГИС непосредственно связан с уровнем ошибок исходных карт • Карты не всегда адекватно изображают информацию и не всегда точно передают данные о местоположении.


МЕТОДЫ ВВОДА ВЕКТОРНЫХ ДАННЫХ Некоторые программы требуют ввода точек в определенной последовательности, в то время как другие этого не требуют.

Многие ошибки оцифровки, особенно у новичков, происходят вследствие нажимания не тех кнопок, что требуется. Одни кнопки используются для указания положения точечных объектов, другие — для обозначения концов прямых отрезков, третьи — для смыкания многоугольников.

Атрибутивные данные в векторных ГИС вводятся чаще всего с использованием клавиатуры компьютера. Хотя этот способ ввода данных предельно прост, он требует такого же внимания, как и ввод графических объектов. Причины две. 1. опечатки совершаются очень легко. 2. атрибуты должны быть связаны с графическими объектами. Ошибки в таком согласовании — одни из наиболее трудных для обнаружения ошибок, поскольку их не всегда можно заметить на взгляд, и они не проявляются до начала выполнения какого нибудь анализа.

МЕТОДЫ ВВОДА РАСТРОВЫХ ДАННЫХ Ввод растровых данных следует иной стратегии, нежели ввод векторных данных. Прежде всего необходимо решить, какую площадь должна занимать каждая ячейка растра. Это решение должно быть принято до начала оцифровки или наложения сетки, чтобы сообщить программе оцифровки размер ячейки или дать оператору сведения о размерах квадратов сетки. Кроме того, следует решить, пригодится ли какой нибудь метод кодирования (типа группового или блочного кодирования), который мог бы сократить процесс. уменьшение объема данных, сокращение времени ввода.

Выбрав метод ввода, вы должны решить, как каждая ячейка растра будет представлять различные имеющиеся темы. Помимо разрешения растра, это может быть наиболее важным мнением, которое должно быть принято.

Результат сканерного ввода в сильной степени зависит от соотношения разрешений сканера и полиграфического растра. Именно сложность решения этой проблемы приводит иногда к решению использовать упомянутый выше способ ввода растровых данных посредством векторной оцифровки контуров объектов с последующим преобразованием в растр.

УСТРОЙСТВА ВВОДА • первый подход к картографическому вводу было использование прозрачного материала с нанесенной сеткой, с помощью которого данные, ячейка за ячейкой, вводились вручную в компьютер. • В большинстве случаев ячейкам растра присваивались числовые значения, которые, опять же вручную, друг за другом вносились в компьютер. • Это требовало применения некоторого правила, определяющего, где внутри ячейки растра помещался вводимый объект. В качестве такой точки может использоваться центр ячейки или любой из четырех ее углов.

Для ручного ввода пространственных данных стандартом является дигитайзер. Он является более совершенным и гораздо более точным родственником наиболее широко используемого графического манипулятора — мыши.

Рабочая поверхность дигитайзера может быть гибкой или жесткой, размерами от книжной страницы до очень больших форматов для размещения больших карт, даже с запасом. Некоторые из крупноформатных дигитайзеров имеют подъемно поворотное основание, позволяющее оператору устанавливать оптимальное для работы положение. Размер стола определяется частично размером вводимых документов.

Для автоматизации ввода карт используются такие устройства, как автоматизированные дигитайзеры и растровые сканеры с программами векторизации или без них.

В состав дигитайзера входят: - электронный планшет, на котором располагают чертеж или карту, предназначенную для оцифровки; - специальный указатель с датчиком, напоминающим увеличительное стекло (лупу) с черным перекрестьем в центре. Электронный графический планшет снабжен собственным контроллером.

Автоматизированные дигитайзеры, или дигитайзеры с отслеживанием линий, имеют устройство, подобное головке оптического считывания проигрывателя компакт дисков. Оно фиксируется на выбранной пользователем линии (как проигрыватель фиксируется на дорожке записи) и, самостоятельно следуя вдоль нее, передает координаты точек линии в компьютер.

Эти устройства требуют постоянного участия оператора, так как их нужно вручную устанавливать на каждую новую линию для продолжения процесса сканирования. Кроме того, они легко могут ошибаться на сложных картах и картах с низкой контрастностью изображения. Например, когда линия расщепляется на две, вполне обычна ситуация, когда сканер не знает, куда идти дальше. Эта проблема может оказаться еще тяжелее, линии изображаются пунктиром, который дигитайзер не может проследить из за разрывов или из за того, что цвет светлее и имеет меньший контраст, чем исходная линия.

В задачи электронной части дигитайзера входит посылка импульсов по сетке проводников, расположенных под плоскостью планшета. Когда импульс проходит под перекрестьем указателя, датчик формирует сигнал, посылаемый контроллеру. Получив два таких сигнала - от горизонтального и вертикального проводников, -контроллер преобразует их в координаты и передает эту информацию в компьютер. Здесь принятая информация переводится в координаты точки на экране монитора, соответствующей положению указателя на планшете. Шаг считывания информации называется разрешением дигитайзера.

По технологии изготовления дигитайзеры делятся на два типа: • электростатические (ЭС) • электромагнитные (ЭМ). В первом случае регистрируется локальное изменение электрического потенциала сетки под курсором. Во втором курсор излучает электромагнитные волны, а сетка служит приемником. (при работе ЭМ планшетов возможны помехи со стороны излучающих устройств, в частности мониторов)



Большее распространение получили растровые сканеры. Они позволяют вводить растровое изображение карты в компьютер без вмешательства человека.

Сами растровые сканеры делятся на ручные, роликовые (с протяжкой листа), планшетные и барабанные. Планшетные сканеры представляют из себя прозрачное стекло, на которое кладется оригинал, и под которым перемещается лампа и устройство оптического считывания. Ручной сканер является, по сути, оптической головкой планшетного сканера, и пользователю приходится самому двигать ее по поверхности оригинала.

Очевидно, что точность сканирования ручных сканеров самая низкая, поэтому устройства этого вида практически не пригодны для ввода карт.

Если карта должна храниться в векторной модели данных, то после сканирования растровое изображение должно быть векторизовано. Векторизация в компьютере выполняется подобно тому, как работает сканер с отслеживанием линий.

Основные характеристики сканеров оптическое разрешение, скорость сканирования стабильность.

Наиболее продвинутые сканеры фотограмметрические. Предназначены для высокоточного сканирования фотоснимков на стеклянной подложке или пленке форматом до 30 х 30 см (используется совместно с цифровой фотограмметрической станцией).


Другой вид сканеров, барабанный карта прикрепляется к барабану, который вращается, в то время как чувствительный датчик прибора перемещается под прямым углом к направлению вращения. Таким образом, сканируется вся карта, линия за линией. Записывается каждое положение на карте, даже если там нет графических объектов. В результате создается подробное растровое изображение всей карты.
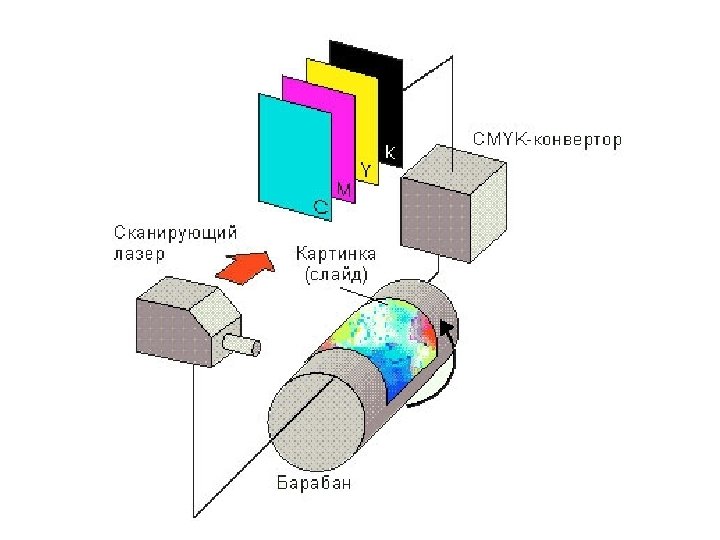

Барабанные сканеры могут давать как монохромное, так и цветное изображение. В последнем случае каждый из основных цветов должен сканироваться по отдельности. Специализированные картографические сканеры большого формата очень дороги по сравнению с дигитайзерами того же формата.

Современные высококачественные планшетные сканеры, будучи намного дешевле и быстрее, практически вытеснили барабанные из областей, связаных с графикой. Тем не менее, барабанные сканеры продолжают использоваться для создания цифровых архивов в музеях, и для других задач, где возможностей обычных сканеров недостаточно.


Для ввода растровых данных наиболее широко применяются сканеры. Однако, следует учитывать, что введенные со сканера тематические данные не становятся автоматически тематическими данными в растровой ГИС.

неоднородность нанесения краски на карту, незаметная для глаз, неоднородность подсветки в сканере, износ карты офсетный способ

Проекции

• Проблема при использовании пространственной информации в ГИС заключается в том, что одна и та же точка на поверхности Земли в различных системах координат, связанных с разными моделями Земли, может иметь разные координаты. • Даже если используется одна модель Земли, но карты составлены в разных проекциях, то часто возникает задача их совместного использования и, следовательно, перевода их всех в одну картографическую проекцию. • Инструментарий для решения именно этих задач определяет важную часть возможностей большинства полнофункциональных ГИС.

• Форма физической поверхности Земли очень сложная. На поверхности Земли встречаются равнины, низменности, возвышенности и горы разной высоты, озера, моря и океаны. • Поэтому для изучения Земли применяют широко известный способ моделирования, или приближения. • В различных исследованиях в качестве модели Земли выступают плоскость, шар, эллипсоид вращения, геоид, квазигеоид Поверхность Земли и ее модели: геоид и эллипсоид

• Если участок поверхности Земли небольшой, то иногда оказы вается возможным применить для этого участка модель плоской поверхности

• В шарообразной модели поверхность Земли имеет сферическую форму, которая определяется лишь радиусом сферы и положением ее центра в теле Земли.

• Модель эллипсоида вращения имеет больше характеристик: раз меры большой и малой полуосей, а также положение центра и ориентация осей эллипсоида относительно оси вращения Земли.

Для более точного описания фигуры Земли используется поня тогеоида или основной уровенной поверхности. • Уровенной поверхностью называется поверхность, всюду перпендикулярная направлениям силы тяжести, а основной уровенной поверхностью, или поверхностью геоида, называется уровенная поверхность, совпадающая с невозмущенной поверхностью Мирового океана и мысленно продолженная под материки. • Такое понятие геоида было введено в XIX в. В действительности моря и океаны, фиксирующие положение основной уровенной поверхности, 1 не имеют единого уровня. • В качестве основной уровенной поверхности принимается поверхность, которая проходит через точку начала отсчета высот, закрепленную на высоте среднего уровня моря.
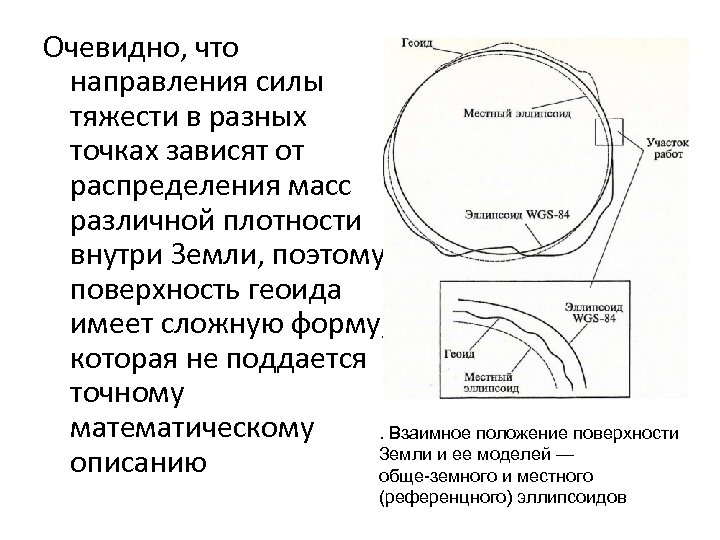
Очевидно, что направления силы тяжести в разных точках зависят от распределения масс различной плотности внутри Земли, поэтому поверхность геоида имеет сложную форму, которая не поддается точному математическому . Взаимное положение поверхности Земли и ее моделей — описанию обще земного и местного (референцного) эллипсоидов

• Отсюда следует, что нельзя задать такой эллипсоид, который наиболее правильно описывал бы всю земную поверхность. Для изучения различных областей используют разные модели эллипсоидов, наиболее точно совпадающих с земной поверхностью в данном районе. • В настоящее время в России и ряде других стран при изучении физической поверхности Земли роль вспомогательной поверхности выполняет поверхность квазигеоида, которая может быть точно определена относительно поверхности эллипсоида по результатам астрономических, геодезических и гравиметрических измерений. на территории морей и океанов поверхность квазигеоида совпадает с поверхностью геоида, а на суше она отклоняется от него в пределах двух метров

• действительную поверхность Земли принимают: на суше — се физическую поверхность, на территории морей и океанов — их невозмущенную поверхность
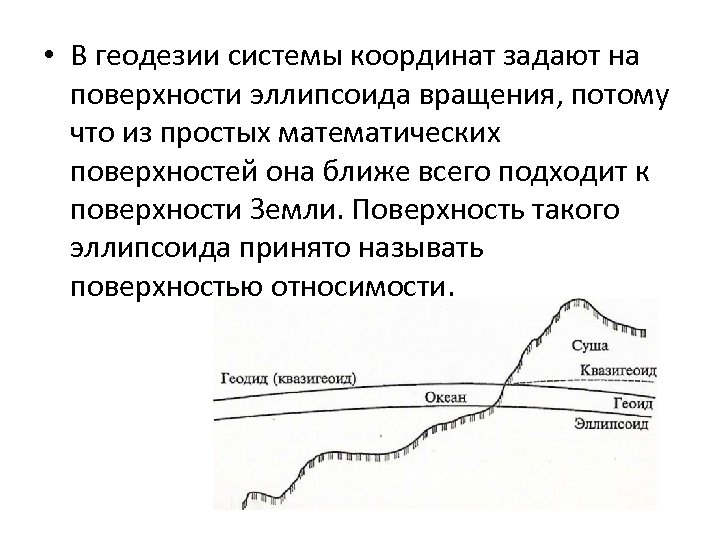
• В геодезии системы координат задают на поверхности эллипсоида вращения, потому что из простых математических поверхностей она ближе всего подходит к поверхности Земли. Поверхность такого эллипсоида принято называть поверхностью относимости.

• Эллипсоид вращения принятых размеров, определенным образом ориентированный в теле Земли, на поверхность которого наносятся геодезические сети при их вычислении, называется референц-эллипсоидом. • В разных странах могут использоваться разные референц эллипсоиды, т. е. эллипсоиды, имеющие различные размеры и различное положение центра относительно центра масс Земли.

• Дли территории нашей страны до 1 июля 2002 г. был принят эллипсоид Красовского. Центр эллипсоида смещен относительно центра масс Земли (х=25; у = -141; z = 80). • Принятый с 1 июля 2002 г. эллипсоид СК-95 является эллипсо идом Красовского: большая полуось а-в 378 245 м, малая полуось b б 356 863 м. Центр эллипсоида смещен относительно центра масс Земли (х = 25, 9; >> = 130, 94; z = 81, 76), а его координатные оси параллельны осям общеземного эллипсоида (ПЗ 90).

• Дли решения космических задач и задач навигации обычно используются общеземные эллипсоиды, т. е. эллипсоиды, центр которых совпадает с центром масс Земли, а полуоси определены так, Чтобы отклонение эллипсоида от геоида было наименьшим. Так, в системе WGS 84 (World Geodetic System) эллипсоид имеет размеры: • большая полуось а = 6 378 137 м, • малая полуось b = 6 356 752 м, • А эллипсоид ПЗ 90, принятый в России, имеет параметры: • а = 6378136 м, • B = 6356751 м.

• • • На поверхности эллипсоида вращения положение точки опре деляется геодезическими координатами — геодезической широтой (В) и геодезической долготой (L). Геодезическая широта точки — угол, образованный нормалью АО' к поверхности эллипсоида в этой точке и плоскостью эква тора. QKQ'. Геодезическая долгота точки — двугранный угол между плоскостью начального меридиана PQP' и плоскостью меридиана точки РАР'. Плоскость геодезического меридиана проходит через точку А и малую ось эллипсоида; в этой плоскости лежит нормаль к по верхности эллипсоида в точке. А. Геодезическая параллель получается в результате пересечения поверхности эллипсоида и плоскостью, проходящей через точку А и параллельной плоскостью экватора . Основные линии географи ч еской системы координа

Картографические проекции • Картографические проекции (КП) — математические способы изображения на плоскости поверхности земного эллипсоида или сферы. • КП определяют зависимость между геодезическими коор динатами точек на поверхности земного эллипсоида и координа тами этих же точек, заданными на плоскости.

• КП строятся в определенном масштабе. Уменьшая мысленно земной эллипсоид в М раз, например в 8 ООО раз, получают его геометрическую модель — глобус, изображение которого уже в натуральную величину на плоскости дает карту поверхности этого эллипсоида. • Величина 1: М (в примере 1: 8 ООО) определяет главный, или общий, масштаб карты, который характеризует ее только в общих чертах — осредненном виде.

• Поскольку поверхности эллипсоида и шара не могут быть раз вернуты на плоскость без растяжений и сжатий, любой КП присущи искажения длин линий, углов, площадей и т. п. • Основная характеристика КП в любой ее точке — частный масштаб р. . Эта величина равна отношению бесконечно малого отрезка da на плоскости к соответствующему бесконечно малому отрезку ds на зем ном эллипсоиде или шаре: • р = da/ds, • причем р зависит от положения точки на эллипсоиде и от направ ления выбранного отрезка.

• Теория КП — математическая картография — имеет своей целью изучение всех видов искажений отображений поверхности зем ного эллипсоида на плоскость и разработку методов построения таких проекций, в которых искажения имели бы или наименьшие значения, или заранее заданное распределение • Изображения меридианов и параллелей в данной КП образуют картографическую сетку. КП может быть определена также двумя уравнениями, в которых в правой части фигурируют не прямоугольные координаты х, у плоскости, а какие либо иные (обычно полярные) координаты.

• Искажения в бесконечно малой области около какой либо точ ки проекции подчиняются некоторым общим законам. Во всякой точке карты в проекции, не являющейся равноугольной, существуют два таких взаимно перпендикулярных направления, которым на отображаемой поверхности соответствуют также взаимно перпендикулярные направления, это — главные направления отображения. • Масштабы по этим направлениям (главные масштабы) имеют экстремальные значения. • Если в какой либо проекции меридианы и параллели на карте пересекаются под прямым углом, то их направления и есть главные для данной проекции.

• Искажения длин в данной точке проекции наглядно представляет эллипс искажений (ЭИ). ЭИ в картографических проекциях — бесконечно малый эллипс в любой точке карты, являющийся ото бражением бесконечно малой окружности в соответствующей точке на поверхности земного эллипсоида или шара. • Полуоси этого эллипса численно равны частным масштабам длин в данной точке в соответствующих направлениях, полуоси эллипса равны экстремальным масштабам, а направления их являются главными направлениями.

Картографические проекции классифицируются: • • • • • по положению полюса сферических координат: нормальные; поперечные; косые; по характеру искажений: равноугольные; равновеликие; равнопромежуточные; произвольные; по виду нормальной сетки меридианов и параллелей: азимутальные; псевдоазимутальные; цилиндрические; псевдоцилиндрические; конические; псевдоконические; поликонические

• Применение тех или иных картографических проекций зависит от назначения карты, конфигурации и положения картографируемой области.

Классификация картографических проекций по положению полюса сферических координат • Полюсы сферы — особые точки географической координации, хотя сфера в этих точках не имеет каких либо особенностей. Значит, при картографировании областей, содержащих географические полюсы, желательно иногда применять не географические координаты, а другие — в которых полюсы оказываются обыкновенными точками координации. • Поэтому на сфере используют сферические координаты, коор динатные линии которых, так называемые вертикалы (условная долгота на них а = const) и альмукантараты (где полярные расстояния z- const), аналогичны географическим меридианам и параллелям, но их полюс Zq не совпадает с географическим полюсом Р 0

• Переход от географических координат любой точки сферы к ее сферическим координатам при заданном положении полюса осуществляется по формулам сферической тригонометрии. • Всякая КП, заданная уравнениями (см выше), называется нормальной (ф0 = π /2) (ось сферических координат совпадает с осью вращения Земли). • Если та же проекция сферы вычисляется по тем же формулам, но ось сферических координат лежит в плоскости экватора, то эта проекция называется поперечной при Фо = 0, и косой (ось сферических координат расположена под углом к земной оси). • нормальная, поперечная и косая ортографические проекции сферы (поверхности шара).

Классификация картографических проекций по характеру искажений • Равноугольные картографические проекции передают на картах углы без искажений и сохраняют в каждой точке постоянный масштаб по всем направлениям (масштаб зависит только от положения точки и не зависит от направления). Например, проекция Меркатора, стереографическая проекция. • В равновеликих КП площади фигур на картах пропорциональны площадям соответствующих фигур в натуре, причем коэффициент пропорциональности — величина, обратная квадрату главного масштаба карты. Эллипсы искажений всегда имеют одинаковую площадь, различаясь формой и ориентировкой. • Произвольные КП — проекции, в которых все перечисленные параметры имеют искажения. • Из них выделяют равнопромежуточные, в которых один из главных масштабов равен единице или другой постоянной величине. • При изображении сферы на плоскости свойства равноугольности, равновеликости, равнопромежуточности несовместимы. •

• • • Классификация нормальных картографических проекций по виду изображений меридианов и параллелей Цилиндрические проекции — проекции, в которых меридианы изображаются равноотстоящими параллельными пря мыми, а параллели прямыми, перпендикулярными к изображе ниям меридианов. Такие проекции выгодны для изображения территорий, вытянутых вдоль экватора или какой либо параллели. II навигации используется проекция Меркатора — равноугольная цилиндрическая проекция. При составлении топографических карт и обработке геодезических измерений применяется проекция Гаусса— Крюгера — равноугольная поперечно цилиндрическая КП.
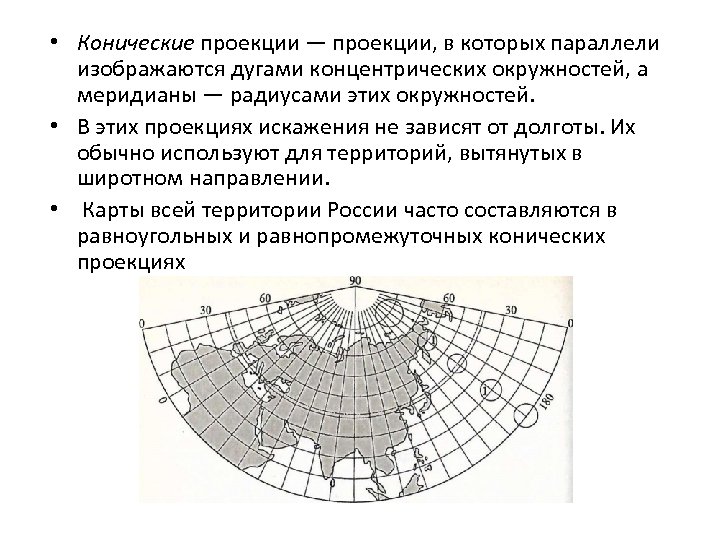
• Конические проекции — проекции, в которых параллели изображаются дугами концентрических окружностей, а меридианы — радиусами этих окружностей. • В этих проекциях искажения не зависят от долготы. Их обычно используют для территорий, вытянутых в широтном направлении. • Карты всей территории России часто составляются в равноугольных и равнопромежуточных конических проекциях
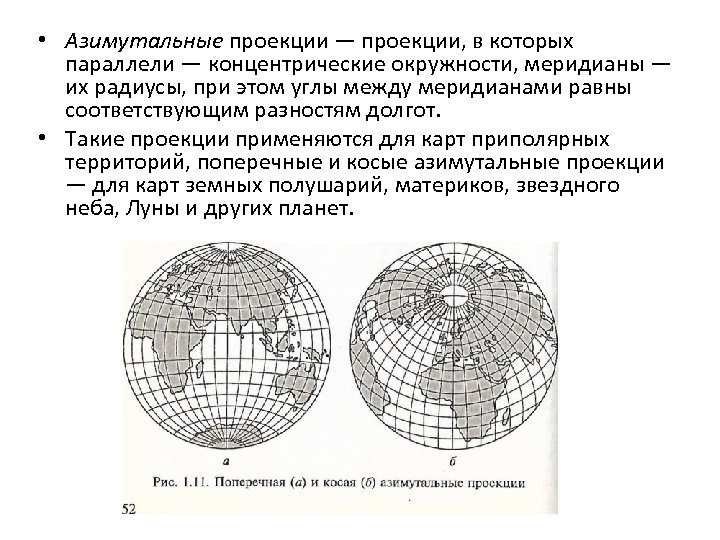
• Азимутальные проекции — проекции, в которых параллели — концентрические окружности, меридианы — их радиусы, при этом углы между меридианами равны соответствующим разностям долгот. • Такие проекции применяются для карт приполярных территорий, поперечные и косые азимутальные проекции — для карт земных полушарий, материков, звездного неба, Луны и других планет.

• В отдельные классы выделяют также псевдоазимутальные, псевдоконические, псевдоцилиндрические, поликонические проекции. Существуют проекции, которые не относятся ни к одному из перечисленных классов. Их иногда называют условными.

• Использование и выбор картографических проекций зависят главным образом от назначения карты и ее масштаба, которыми часто обусловливается характер допускаемых искажений в избираемой КП. • Карты крупных и средних масштабов, предназначенные для решения метрических задач, обычно составляют в равноуголь ных проекциях, а карты мелких масштабов, используемые для общих обозрений и определения соотношения площадей каких либо территорий, — в равновеликих. • При этом возможно некоторое нарушение определяющих условий этих проекций, не приводящее к ощутимым погрешностям, т. е. допустим выбор произвольных проекций, из которых чаще применяют проекции равнопромежуточные по меридианам. К последним прибегают и в тех случаях, когда назначением карты вообще не предусмотрено сохранение углов или площадей

• Значительное количество карт составлено в проекциях Меркатора и Гаусса—Крюгера

• Проекция Меркатора. Является равноугольной цилиндрической, характеристическое свойство которой состоит в том, что все локсодромии (линии на сфере, пересекающие все меридианы под одним и тем же углом) изображаются прямыми, наклоненными к изображениям меридианов под тем же самым углом. • Такая проекции широко используется в морской навигации и в аэронавигации. И этой проекции Г. Меркатор создал первую многолистную карту Мира (1569), хотя сетки равноугольной цилиндрической проекции строились и до него.

• Проекция Гаусса—Крюгера. Разделяет всю поверхность Земли условно на 60 зон меридианами, проведенными через 6°; форма зоны — сферический двуугольник; счет зон ведется от Гринвичского меридиана на восток. Средний меридиан зоны называется осевым; Представим, что земной эллипсоид вписан в эллиптический цилиндр. Ось цилиндра расположена в плоскости экватора и проходит через центр эллипсоида. •

• Цилиндр касается эллипсоида по осевому меридиану данной зоны. Вся поверхность зоны проецируется на поверхность цилиндра при соблюдении условия равноугольности, т. е. углы в ней не искажаются. • Для территории нашей страны искажения длин линий находят ся в допустимых пределах для карт масштабов 1: 10 ООО и мельче; для карт масштаба 1: 5000 и крупнее приходится применять трех градусные зоны. • Поверхность цилиндра разрезается и развертывается на плос кости; при этом осевой меридиан и экватор изображаются в виде двух взаимно перпендикулярных прямых линий.

• • • Arc. View GIS Пространственные данные, хранящиеся в десятичных градусах (градусах и долях градуса) долготы и широты, можно отображать в окне карты в любой из имеющихся в Arc. View картографической проекции. Для вызова мастера выбора проекции отображения и задания ее параметров необходимо выполнить команду Вид > Свойства > Проекция. В этом мастере можно выбрать стандартную проекцию (с пол ностью определенными параметрами) или осуществить настройку параметров, в том числе выбрать эллипсоид. Перечень стандартных эллипсоидов достаточно широк

• • Maplnfo Стандартной проекцией, используемой в Maplnfo, также является проекция широта/долгота, т. е. равнопромежуточная цилиндрическая проекция. Любая таблица карты в Maplnfo содержится в определенной проекции. При показе таблицы в окне карты может быть выполнен пересчет в другую проекцию (без изменения данных в таблице). Выбор новой проекции для окна карты осуществляется в пункте меню Карта > Режимы. При открытии нового окна карты, содержащей несколько таблиц, Maplnfo будет отображать карту, используя проекцию самого верхнего слоя. В Maplnfo можно создать копию таблицы в другой проекции. Для этого выбирается команда Файл > Создать копию.
3931deb264c042a484f3ce29ae1e5c3d.ppt