Введение в вычислительную математику 1 Этапы вычислительного эксперимента

Введение в вычислительную математику 1. Этапы вычислительного эксперимента. 2. Точность вычислительного эксперимента (ВЭ). 2. 1 Понятие погрешности. 2. 2 Классификация погрешностей ВЭ 3. Требования к вычислительным методам.

Этапы вычислительного эксперимента (ВЭ) (основные определения) Предметная область вычислительной математики: • математическое моделирование; • вычислительный эксперимент. Вычислительный эксперимент — метод исследования сложных проблем, основанный на построении математических моделей для изучаемых объектов и анализе этих моделей с помощь ЭВМ. Численный метод — Такая интерпретация математической модели ( «дискретная модель» ), которая доступна для реализации на ЭВМ. Результат реализации численного метода — число или таблица чисел. содержание

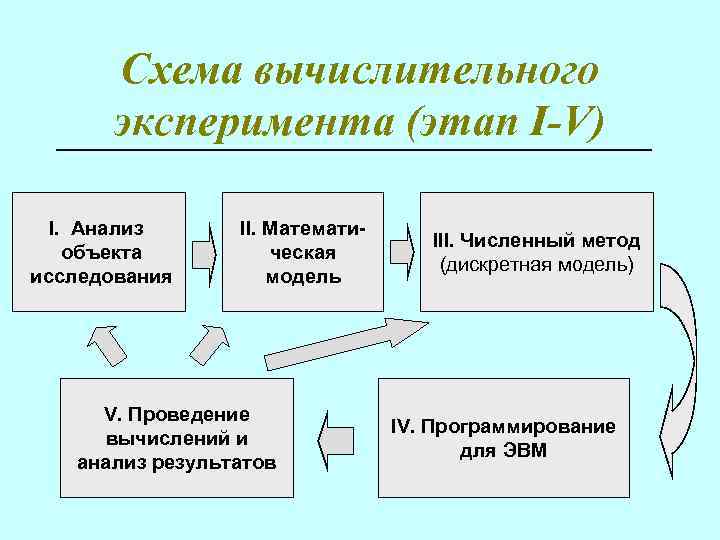Схема вычислительного эксперимента (этап I-V) I. Анализ объекта исследования II. Математическая модель V. Проведение вычислений и анализ результатов III. Численный метод (дискретная модель) IV. Программирование для ЭВМ

2. Точность вычислительного эксперимента Понятие погрешности. Абсолютная погрешность: Dx = x - a где x — истинное значение величины. a — приближенное значение величины. Относительная погрешность dx=Dx/x Предельные погрешности: • абсолютная Da ³ ½D x½ • относительная da ³ Da / ½a½ Þ x Î (a - Da , a + Da) содержание

Классификация погрешностей ВЭ • неустранимые погрешности (погрешности II этапа, связанные с упрощение исходного явления); • погрешности метода (регулируемые погрешности) погрешности дискретизации округления

Требования к вычислительным методам Дискретная модель (численный метод) должна быть: • устойчивой; • корректной; • сходящейся. содержание

Устойчивость Задача называется устойчивой по параметру x, если её решение y непрерывно от него зависит, т. е. малое приращение исходной величины Dx вызывает малое приращение Dy Dy = y – y, где y = A (x + Dx )

Корректность Задача называется корректно поставленной, если для любых значений исходных данных из некоторого класса её решение существует, единственно и устойчиво по исходным данным. Идея регуляризации: • исходная задача заменяется корректно поставленной, в составе которой есть некоторый параметр, • при стремлении данного параметра к нулю решение этой задачи переходит в решение исходной задачи.

Сходимость численного метода означает близость полученного численного решения к исходному. Сходимость итерационного процесса Итерационный процесс состоит в том, что для решения некоторой задачи строится последовательные приближения x 1 , x 2 , x 3 , . . . , xn , . . . Говорят, что эта последовательность сходится, существует если lim xn = a сходимость метода дискретизации означает стремление значений n®¥ дискретной задачи к решению исходной при стремлении к нулю параметра дискретизации.