ВВЕДЕНИЕ В ТЕОРИЮ КОЛЕБАНИЙ Примем в качестве общего

Зарегистрируйтесь, чтобы просмотреть полный документ!

ВВЕДЕНИЕ В ТЕОРИЮ КОЛЕБАНИЙ Примем в качестве общего определения колебаний следующее: это любой знакопеременный процесс, обладающий свойством повторяемости. Исходя из этого определения можно указать бесконечное множество типов колебания: механические, электромагнитные, химические, биологические, наконец, политические колебания, к исследованию которых часто применимы общие закономерности. Инженера-механика, несомненно, интересуют в первую очередь механические колебания. В настоящее время имеется стандартизованное определение механических колебаний: это такое движение механической системы, при котором хотя бы одна обобщенная координата или ее производная по времени поочередно возрастает и убывает.

Причины изучения колебаний В наше время на исследования различных типов колебаний затрачиваются большие средства. В некоторых случаях, когда колебания желательны, исследования ведутся в целях их регулирования. Чаще задача заключается в выяснении причин возникновения колебаний и их предотвращении, если это возможно. Обобщая обстоятельства, при которых инженер учитывает, будет ли роль колебательного процесса существенной для проектируемого объекта, можно выделить следующие причины повышенного внимания к колебаниям: 1. Устранение аварийных режимов. 2. Обеспечение точности выполнения процесса. 3. Обеспечение необходимого срока эксплуатации.

4. Обеспечение технологического процесса, использующего колебательные процессы. 5. Защита человека-оператора от вредного влияния колебаний на организм. К аварийным режимам, возникающим вследствие колебаний, следует отнести резонансные разрушения. Такой тип разрушения обычно столь же катастрофичен, сколь и неожидан. Широко известен пример разрушения моста при прохождении взвода солдат, разрушение потолка помещения одной из дореволюционных государственных дум. В настоящее время актуально предотвращение опасных автоколебаний различных высотных сооружений и быстролетящих объектов. Точность технологических процессов, например, точность обработки изделия на металлорежущем станке, также зависит во многом от процесса колебаний режущего инструмента и самой детали, закрепленной в приспособлении.

Электронную аппаратуру самолетов и ракет часто приходится устанавливать на специальные виброизолирующие опоры для того, чтобы колебания частей самолета или ракеты не повлияли на ее работу. Проблемой для точного наведения подводных лодок на курс является вибрация ее перископа. Влияние колебаний на уменьшение сроков эксплуатации изделий сказывается из-за усталости материала. Известно, что если образец какого-либо материала выдерживает определенную однократную нагрузку, то при нескольких нагружениях разрушающая нагрузка уменьшается и зависит от количества и характера циклов нагружения. Если гайка навернута на болт, находящийся под действием переменной нагрузки, то возможно ослабление соединения, поэтому в этом случае следует предусмотреть и предотвратить самоотвинчивание. Явление усталостного разрушения связано с наличием высоких местных напряжений, причем во многих случаях эти напряжения неизбежны.

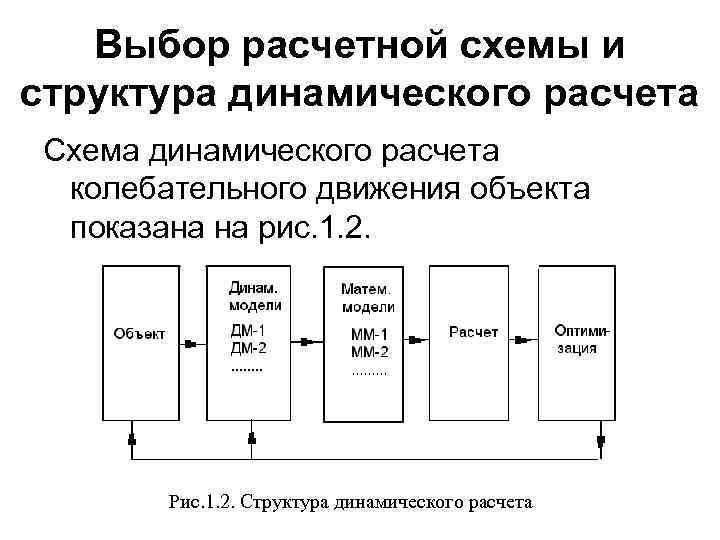
Выбор расчетной схемы и структура динамического расчета Схема динамического расчета колебательного движения объекта показана на рис. 1. 2. Рис. 1. 2. Структура динамического расчета

На основе исследуемого объекта составляются его динамические модели. Они представляют собой взаимосвязанные между собой и с внешними связями упругими и диссипативными элементами инерционные элементы, к которым приложены возмущающие нагрузки. Инерционные элементы представляют собой материальные точки, имеющие массы и тела, имеющие массу и момент инерции (или только момент инерции) - рис. 1. 3. m (J) а)линейные б)угловые Рис. 1. 3. Инерционные элементы (Н. /М) С(НМ) Рис. 1. 4. Жесткостные элементы (характеристики) изображены на рис. 1. 4. Линейные жесткости имеют размерность силы/перемещения, а угловые - момента.

Показанные жесткости имеют линейный характер, когда восстанавливающая сила (момент) пропорциональна перемещению, но могут быть и более сложные элементы с нелинейными восстанавливающими силами Наличие в объекте диссипативных сил сопротивления (зависящих от скорости) отражается в схеме диссипативными элементами - рис. 1. 5. Рис. 1. 5. Элементы трения Такие элементы также могут иметь нелинейные характеристики. Возмущающие силы могут иметь различный источник возникновения - электромагниты, давление газов. В некоторых случаях возмущающие силы представляют собой случайный процесс (сейсмические нагрузки, действие неровной дороги, волнение водной поверхности).

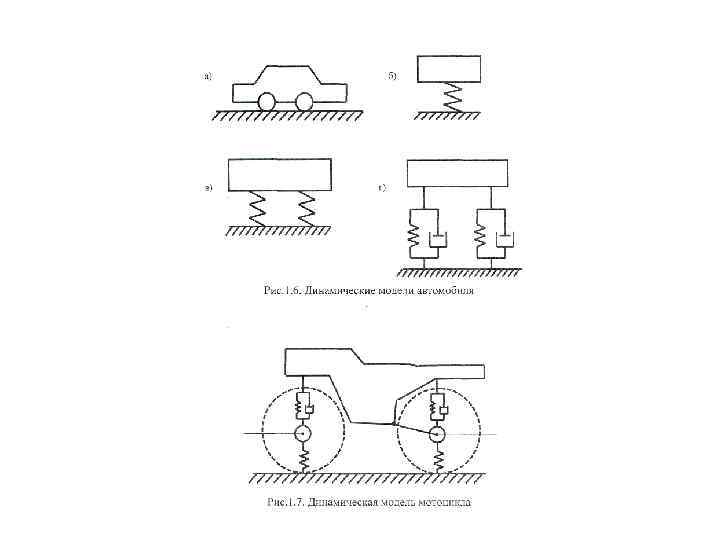
Характеристики таких случайных процессов (математическое ожидание, дисперсия, корреляционная функция) получаются путем обработки экспериментальных данных. Для любого объекта можно составить несколько динамических моделей, отражающих его свойства в разной степени. Обычно начинают с наиболее простой схемы, последовательно усложняя ее путем введения дополнительных элементов и разбивая его на более мелкие части. Несколько динамических моделей автомобиля изображено на рис. 1. 6. На рис. 1. 7 изображена схема динамической модели мотоцикла. После составления динамических моделей переходят к составлению математических моделей, то есть дифференциальных уравнений, которые решаются аналитическими или численными методами. Естественно, что с усложнением динамических моделей существенно возрастает трудность решения уравнений, но не нужно чрезмерно усложнять расчетную схему.

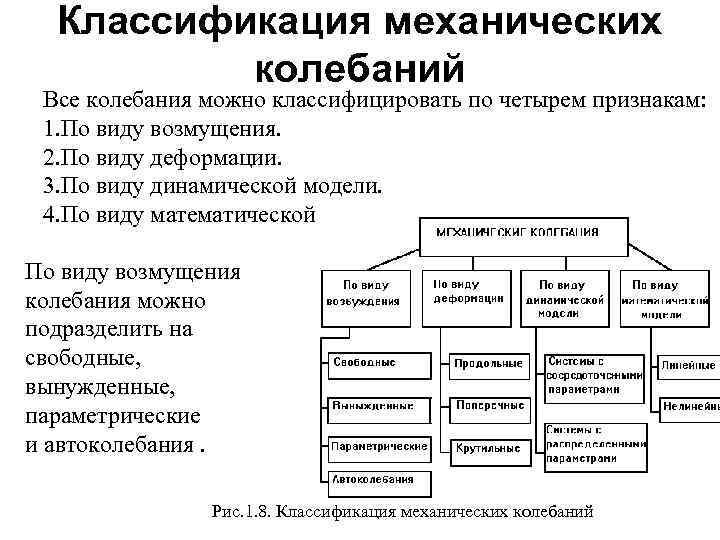
Классификация механических колебаний Все колебания можно классифицировать по четырем признакам: 1. По виду возмущения. 2. По виду деформации. 3. По виду динамической модели. 4. По виду математической модели. По виду возмущения колебания можно подразделить на свободные, вынужденные, параметрические и автоколебания. Рис. 1. 8. Классификация механических колебаний

Свободными (собственными) колебаниями называются такие, при которых энергия в систему вносится один раз в начале процесса, то есть либо изменяется потенциальная энергия путем сообщения начального отклонения, либо кинетическая - с помощью толчка сообщается начальная скорость. В дальнейшем система предоставлена самой себе. Пример - колебания грузика на пружине, маятник (рис. 1. 9. ) Вынужденные колебания вызываются произвольно изменяющимися силами, например периодическими (в частном случае –гармоническими). Энергия вносится в течение всего процесса. Возбуждение может быть силовым (например, на рис. 1. 10. колебания балки вызываются периодически изменяющимися силами инерции) и кинематическим (рис. 1. 11. ), когда перемещается точка подвеса.

Параметрические колебания вызываются периодическими изменениями инерционных или жесткостных параметров самой системы и возникают в сравнительно узком диапазоне частот. Примером их может быть самораскачивание качелей, когда человек, находящийся на них, приседая и распрямляясь, периодически изменяет их инерционную характеристику, а также колебания шахтных подъемников, вызванные изменением жесткости рельсов между опорами. Автоколебания являются признаком нелинейных систем, это свободные колебания нелинейных систем, которые вызываются силами от энергетического источника неколебательного характера. Такими силами могут быть силы тяжести (часыходики, приводимые в движение гирей), силами трения (рис. 1. 12. ) - горизонтальные автоколебания упругого закрепленного груза, находящегося на движущейся бесконечной ленте, силами сопротивления среды (флаттер крыльев самолета - рис. 1. 13. ).

По виду деформации колебания подразделяются на продольные, поперечные и крутильные. Продольными называются такие колебательные движения, направление которых совпадает с осью упругого элемента. Пример - колебания грузика на пружине. Поперечные - это колебания, при которых ось упругого элемента перпендикулярна перемещению, например поперечные колебания балок (рис. 1. 14. ). Крутильные - те, которые приводят к изменению угла поворота тела (рис. 1. 15. ). По виду динамической модели различают системы с сосредоточенными параметрами, которые имеют конечное число степеней свободы, и системы с распределенными параметрами, имеющие бесконечное число степеней свободы.

Числом степеней свободы механической системы называют число взаимно независимых величин (обобщенных координат), однозначно определяющих положение всех материальных точек системы в любой момент времени. Хотя для реальных систем это число всегда бесконечно велико, но в ряде случаев практически достаточен учет конечного числа существенных степеней свободы. При схематизации системы наиболее легкие элементы полагают вовсе лишенными массы, сравнительно жесткие части считают вообще не деформируемыми, а отдельные малые тела представляют в виде материальных точек. При формировании динамических моделей задачей является приведение распределенных масс к системам с ограниченным количеством степеней свободы. Например, балку заменить материальной точкой, находящейся посередине ее пролета и закрепленной на опорах при помощи невесомого стержня (рис. 1. 16. ).

Рис. 1. 16. Приведение распределенной системы к точечной массе Исходим из равенства кинетических энергий. Для материальной точки Для элемента балки где m - погонная масса. Отсюда Предположим, что балка изогнута по синусоиде

После подстановки получим После интегрирования получим: M = ml/2. Таким образом, масса груза равна половине массы балки. Введение элементов трения в механическую систему иногда приводит к изменению числа степеней свободы и образованию систем с нецелым числом степеней свободы /2/. Системами с распределенной массой являются стержни, пластины, оболочки и т. д. , так как в каждый момент времени конфигурация их определяется не конечным числом параметров, а является функцией пространственной системы координат. Примеры непрерывно деформируемых систем с распределенными параметрами приведены в табл. 1.

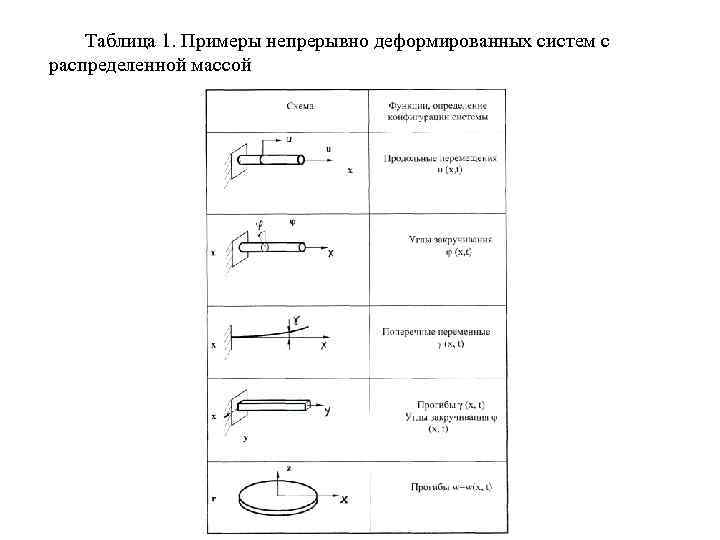
Таблица 1. Примеры непрерывно деформированных систем с распределенной массой

По виду математической модели различают линейные колебания и нелинейные. Линейными являются системы, движение которых характеризуются линейными дифференциальными уравнениями. Это будет наблюдаться, если упругие элементы имеют линейные характеристики, а силы сопротивления пропорциональны первой степени скорости. Нелинейность механической системы может быть обусловлена нелинейностью упругой характеристики или характеристики трения. В последнем случае различают диссипативные системы и фрикционные автоколебательные системы. В диссипативных системах трение является причиной рассеивания энергии, а в автоколебательных системах благодаря силам трения происходит приток энергии в систему (схема на рис. 1. 12). Типичные характеристики нелинейных упругих элементов приведены в табл. 2, а характеристики трения - в табл. 3.

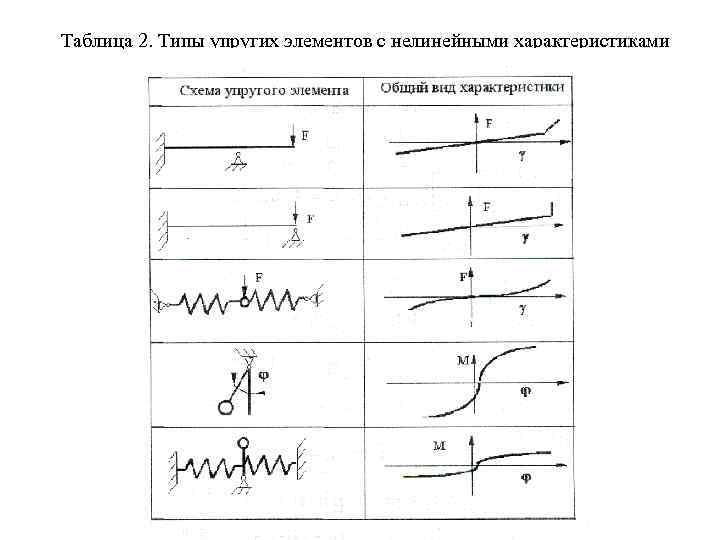
Таблица 2. Типы упругих элементов с нелинейными характеристиками

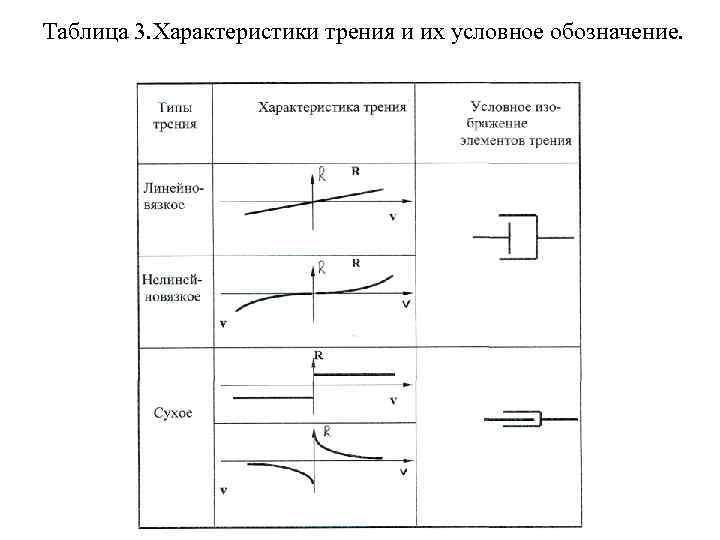
Таблица 3. Характеристики трения и их условное обозначение.

ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ РАВНОВЕСИЯ Со словом “ устойчивость” можно встретиться довольно часто не только в механике, но и в повседневной жизни, например: “ морально устойчивый человек”, “ пшеница дает устойчивый урожай”, “автомобиль устойчив в управлении” и так далее. Окружающий нас мир полон примеров устойчивого и неустойчивого. Многого мы не замечаем - порой, по неосведомленности, а то и по невнимательности. Устойчивым называется такое состояние, процесс, предмет, при которых малые отклонения естественных входов приводят к малым отклонениям естественных выходов ( в данном конкретном отношении). Процесс называется неустойчивым, если малые отклонения естественных входов приводят к большим отклонениям естественных выходов.

Понятие об устойчивости равновесия в механике • Состояние равновесия механической системы называется устойчивым, если , будучи выведенной из этого состояния , система стремится вернуться в первоначальное положение и совершает относительно его колебательное движение например шарик на внутренней поверхности цилиндра (рис. 2. 4, а. ). • Состояние равновесия механической системы называется неустойчивым, если , будучи выведенной из этого состояния , система никогда не вернется в прежнее положение (рис. 2. 4, б. ). • Состояние равновесия называется безразличным, если выведенная из равновесия система и в новом положении будет в равновесии (рис. 2. 4, в. ).

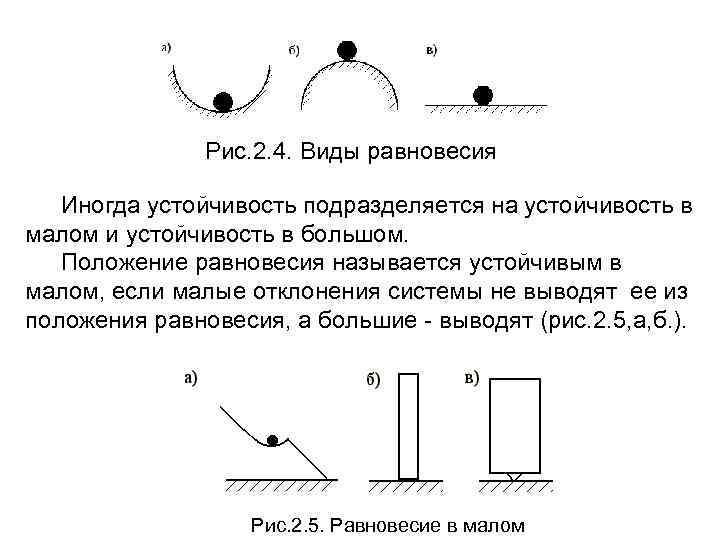
Рис. 2. 4. Виды равновесия Иногда устойчивость подразделяется на устойчивость в малом и устойчивость в большом. Положение равновесия называется устойчивым в малом, если малые отклонения системы не выводят ее из положения равновесия, а большие выводят (рис. 2. 5, а, б. ). Рис. 2. 5. Равновесие в малом

Положение равновесия называется устойчивым в большом, если любые отклонения системы не выводят ее из положения равновесия. Равновесие может быть одновременно устойчивым и в большом и в малом (рис. 2. 4, а. ), только в малом и даже неустойчивым в малом , но устойчивым в большом (рис. 2. 5, в. ).

Математическое определение устойчивости (устойчивость по Ляпунову) При определении условий равновесия механической системы возникает вопрос о практической реализации этих условий. Математически это условие было поставлено А. М. Ляпуновым: равновесие системы в данном положении называется устойчивым, если ее можно вывести из этого настолько малым возмущением ( смещением, толчком), что во все последующее время отклонение системы от положения равновесия будут меньше любого, сколь угодно малого отклонения. Это условие, выраженное в обобщенных координатах для системы с S cтепенями свободы имеет вид: (2. 1)

Если при устойчивом равновесии все координаты и скорости с течением времени стремятся к нулю, то рассматриваемое положение равновесия называется асимптотически устойчивым. Один общий критерий, устанавливающий достаточное условие устойчивости равновесия консервативной системы, дает теорема Лагранжа-Дирихле: если потенциальная энергия системы имеет в положении равновесия строгий минимум, то равновесие является устойчивым. Даваемое теоремой условие устойчивости равновесия является, однако, лишь достаточным и не позволяет судить о том, что будет, если в положении равновесия потенциальная энергия не имеет минимума. Рассмотрим систему с одной степенью свободы. Выберем, что в положении равновесия обобщенная координата системы равна нулю: q=0. Тогда условие минимума потенциальной энергии (2. 2)

Кроме того, в положении равновесия обобщенная сила должна быть равна нулю, то есть выполняется условие (2. 3) Пример 1. Определить, в каком положении невесомый стержень ОА длиной L, на конце которого находится точечный груз массой m, будет находиться в положении устойчивого равновесия (рис. 2. 6. ). В качестве обобщенной координаты выберем угол поворота стержня, отсчитывая его от вертикали. Потенциальная энергия в произвольном положении системы равна работе, которую совершают силы при перемещении системы из данного положения в нулевое. Рис. 2. 6. Схема к примеру 1

Выбрав за нулевой уровень нижнее положение груза, име П = mg. L(1 -cos ). Отсюда: Следовательно, стержень может находиться в равновесии в двух случаях: =0 и =180 о , то есть и в нижнем, и в верхнем положении. Исследуем, в каком случае равновесие устойчиво. Для этого найдем вторую производную от потенциальной энергии по обобщенной координате: При =0 сos =1 то есть положение равновесия будет устойчивым.

При =180 сos =1, а то есть положение равновесия неустойчиво, поскольку условие (2. 2) не выполняется. Пример 2. Определить условия, при которых стержень AD (рис. 2. 7, а. ), прикрепленный к двум пружинам, будет находиться в положении устойчивого равновесия, если его масса m, длина L, расстояние от оси вращения до точки крепления пружин АВ=h, жесткости пружин с1 и с2 , их начальные деформации равны и соответственно. В качестве обобщенной координаты выберем угол поворота стержня от вертикали (рис. 2. 7, б. ). Потенциальная энергия в произвольном положении системы будет равна: П=П 1+П 2, , где потенциальная энергия стержня,

П 2=0, 5[c 1( +h )2 +c 1( -h )2 ] потенциальная энергия пружин. Рис. 2. 7. Схема к примеру 2 При нахождении потенциальной энергии полагаем угол малым, то есть cos =1 Раскрывая скобки и суммируя все слагаемые, представим выражение для потенциальной энергии в виде

где П 0 включает все величины, не зависящие от . Отсюда находим Для того, чтобы стержень находился в равновесии при =0, эта производная должна быть равна нулю, что выполнимо при с1 2 =c Далее находим вторую производную: Для того, чтобы положение равновесия было устойчивое, это выражение должно быть положительным , то есть выполнялось условие

УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА Для исследования колебательных процессов удобно использовать уравнения Лагранжа второго рода, которые являются универсальным инструментом для решения большого количества задач движения механических систем. В инженерной практике, как правило, приходится иметь дело с системами, на которые наложены связи. Например, твердое тело – связанная система точек, расстояния между которыми не изменяются. Любой механизм: лебедка, домкрат, редуктор скоростей и др. – все это системы связанных между собою тел.

Связями механической системы называются любые ограничения, накладываемые на координаты и скорости точек этой системы. Аналитически связи могут быть представлены уравнениями (или неравенствами), которым должны удовлетворять координаты точек системы и производные от координат по времени. Для исследования движения, в отличие от статики, неважно, какими телами осуществляется связь. Существенно то, какие ограничения на движение системы она налагает. Далее будут рассматриваться такие механические системы, на которые наложены только голономные, стационарные и чаще всего удерживающие и идеальные связи. Определим эти классы связей. Геометрическими называются связи, которые накладывают ограничения на координаты точек. Обычно это различного рода закрепления точек системы: подшипники, шарниры, опорные поверхности и т. д.

Такие связи можно подразделить на односторонние и двусторонние. Двусторонними или удерживающими называются связи, препятствующие перемещению в двух взаимно противоположных направлениях. К ним относится, например, тонкий невесомый стержень (рис. 3. 1, в). Односторонними (неудерживающими) называются связи, препятствующие перемещению в одном направлении, например, гибкая связь. Стационарными называются связи, не зависящие явно от времени. В этом случае время в уравнение связей не входит. Нестационарные это связи, зависящие от времени. Связи, которые накладывают ограничения на скорости точек, называются кинематическими или дифференциальными. Они подразделяются на интегрируемые и неинтегрируемые.

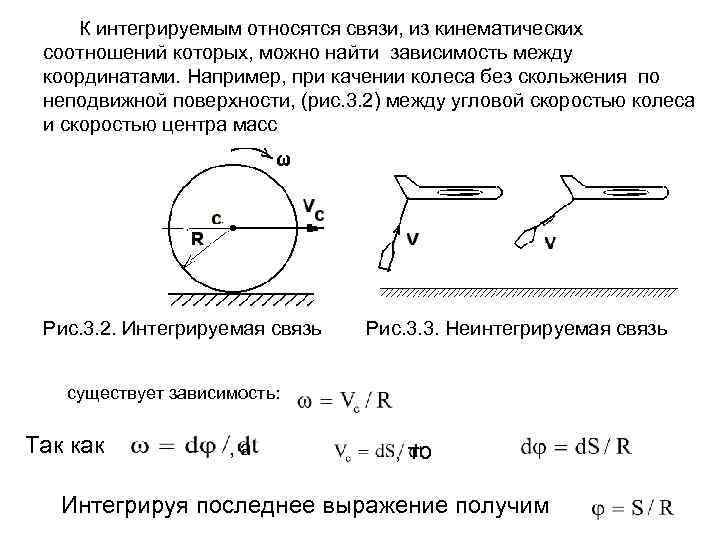
К интегрируемым относятся связи, из кинематических соотношений которых, можно найти зависимость между координатами. Например, при качении колеса без скольжения по неподвижной поверхности, (рис. 3. 2) между угловой скоростью колеса и скоростью центра масс Рис. 3. 2. Интегрируемая связь Рис. 3. 3. Неинтегрируемая связь существует зависимость: Так как , а , то Интегрируя последнее выражение получим

Неинтегрируемыми называются связи, в уравнениях которых из зависимостей между скоростями нельзя найти зависимости между перемещениями. К таким связей относятся следящие системы, например, система наведения ракет “ земля воздух “ (рис. 3. 3) , шар на плоскости и т. д. . Геометрические и интегрируемые кинематические связи называются голономными, а механические системы, на которые наложены только такие связи голономными системами. В общем виде данные связи представляются уравнениями: (k=1, 2, . . . , m; m < 3 N), N - число точек системы.

Возможные перемещения. • В механических системах при отсутствии связей любые перемещения точек не ограничены, то есть возможны. Иначе обстоит дело в системах, на которые наложены связи. Например, в твердом теле любому перемещению одной точки будут соответствовать определенные перемещения всех остальных точек. Аналогично и в механизмах, представляющих собою системы взаимосвязанных тел. • Возможными (виртуальными) перемещениями системы называют воображаемые, бесконечно малые перемещения, допускаемые связями в данный момент времени. • Обозначения: • возможные перемещения точек системы; • действительные перемещения точек. • В примерах, показанных на рис. 3. 1, возможным перемещением поршня является его поворот вокруг оси Oz на угол. • Если связи со временем не изменяются (стационарны), то любое действительное перемещение может произойти из числа возможных. В случае односторонних (неудерживающих) связей к числу возможных относят лишь такие перемещения, при которых точки системы не покидают связь.

Число степеней свободы. Числом степеней свободы механических систем называют число взаимно независимых возможных перемещений. Рис. 3. 5. Независимые перемещения точки Пусть механическая система состоит из “n” точек, на которые наложено “k” связей. Каждая свободная точка имеет три независимых перемещения: xi, yi, zi (рис. 3. 5). Все “n” точек, будучи не связанными, имели бы 3 n независимых перемещений. Так как эти 3 n перемещений взаимосвязаны “k” условиями связей, то независимых перемещений остается: S = 3 n – k, (3. 1) где S – число независимых перемещений, или, по определению, число степеней свободы.

Давая независимые возможные перемещения, легко определить, что твердое тело может иметь следующие числа степеней свободы: при вращении вокруг неподвижной оси – одну, при поступательном движении – три, при плоскопараллельном – три, при сферическом – три; свободное твердое тело имеет шесть степеней свободы. Как известно, число статических условий равновесия и кинематических уравнений движения твердого тела всегда равно числу его степеней свободы. Ниже будет показано, что аналогичное соответствие имеет место и в динамике механических систем, состоящих из совокупности взаимодействующих тел.

Возможная работа. Возможной работой называют работу силы на возможном перемещении (3. 2) Из определения возможных перемещений следует, что возможная работа это воображаемая и бесконечно малая. Вычисляется она точно так же, как и действительная элементарная работа: (3. 2') Как и на действительных, на возможных перемещениях можно подсчитывать работу как активных, так и пассивных сил, а при необходимости ещё и возможную работу даламберовых сил инерции.

Идеальные связи. • Идеальными называют такие связи, у которых сумма работ сил реакций равна нулю на любом возможном перемещении: (3. 3) где i – номер силы реакции.

О целесообразности обобщенных координат. • Допустим, что требуется рассмотреть движение или равно весие механической системы, состоящей из "n" материаль ных точек, на которую наложено "k" связей. При выполнении решения в декартовых координатах пришлось бы составить систему "3 n" уравнений. Но эти уравнения не являются независимыми, они связаны "k" уравнениями. Следовательно, число независимых уравнений, определяющие состояние всей системы, будет равно: 3 n – k.

Понятие обобщенных координат. Обобщенными координатами называют взаимно независимые параметры, однозначно определяющие положение всей системы. • Так как число независимых перемещений системы равно числу степеней свободы, то и обобщенных координат системы всегда равно столько, сколько степеней свободы. Обозначения: • q 1; q 2; …; q. S. т. е. qj; j = 1, 2, …, S, • где j номер степени свободы. • Размерность обобщенных координат может быть самой различной. В механике чаще всего за обобщенные координаты принимают расстояния или углы поворотов.

Кинематические уравнения движения. • Если механическая система движется, то обобщенные координаты, оставаясь взаимно независимыми, изменяются с тече нием времени, т. е. являются функциями времени: • qj = qj(t); j = 1, 2, …, S. (3. 6) • (3. 6) это и есть кинематические уравнения движения в обобщенных координатах. Их число всегда равно числу степеней свободы. Векторные уравнения движения всех точек системы примут вид: (3. 7) • где i = 1, 2, …, n (точек), j = 1, 2, …, S (степеней свободы).

КОЛЕБАНИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ Вычисление кинетической энергии механической системы • Для исследования колебательных процессов удобно использовать уравнения Лагранжа второго рода. В уравнения Лагранжа входят величины кинетической и потенциальной энергии системы. Учитывая, что дифференцирование по обобщенной координате qi и обобщенной скорости снижает порядок малости на единицу, значения Т и П следует вычислять с точностью до малых величин второго порядка малости. Выражение для потенциальной энергии было получено в разделе 2. • Для вычисления кинетической энергии отметим, что для голономной механической системы со стационарными связями, имеющей S степеней свободы, радиус вектор любой точки системы является функцией S обобщенных

Следовательно, скорость каждой точки системы Вычисляем кинетическую энергию системы Из этого выражения видно, что кинетическая энергия Т является однородной квадратичной функцией обобщенных скоростей с коэффициентами, зависящими от обобщенных координат.

В этом выражении При этом Аij=Aji. Разлагая каждый из этих коэффициентов в рад Маклорена по степеням обобщенных координат , получаем Индекс 0 соответствует значениям функции в положении равновесия.

Так как рассматриваются малые отклонения системы от положения равновесия, то можно ограничиться только первыми постоянными членами: (Аij)0=Aij(0, 0, . . . , 0). Обозначая эти постоянные через аij имеем или в общем виде (4. 1) Постоянные аij называются коэффициентами инерции. Для системы с одной степенью свободы формула (4. 1) примет вид c двумя: и так далее.

Свободные колебания системы с одной степенью свободы при отсутствии сил сопротивления • Рассмотрим движение механической системы с одной степенью свободы , на которую наложены голономные, стационарные и идеальные связи, около положения устойчивого равновесия под действием только восстанавливающей силы. • Кинетическая Т и потенциальная П энергия системы в этом случае определяются выражениями • Простейшим аналогом такой системы является груз, прикрепленный к пружине и расположенный на гладкой горизонтальной поверхности (рис. 4. 1. ), при этом, если в качестве обобщенной координаты возьмем перемещение груза Х, отсчитываемое от его положения равновесия, кинетическая энергия будет равна

то есть коэффициент потенциальная энергия: где m - масса груза, а с - жесткость пружины. Рис. 4. 1. Пример системы с одной степенью свободы Для исследования движения системы применим уравнение Лагранжа 2 рода: Тогда слагаемые, входящие в это уравнение, будут равны.

и уравнение примет вид. Полагая с/a=k 2, получим: (4. 2) Выражение (4. 2) называется дифференциальным уравнением свободных колебаний системы с одной степенью свободы. Общее решение уравнения (4. 2) имеет вид (4. 3) откуда . Для определения постоянных интегрирования необходимы начальные условия. Допустим, что при Тогда

Подставляя эти значения в уравнение (4. 3), получим (4. 4) Как видно, в этом случае колебание зависит от двух частей: колебаний, которые пропорциональны coskt и зависят от начального смещения, и колебаний , которые пропорциональны sinkt и зависят от начальной скорости. Каждая из этих частей может быть представлена графически (рис. 4. 2. , а и б. ). Рис. 4. 2. Составляющие колебания

Если в уравнении (4. 3) вместо постоянных С 1 и С 2 подставить постоянные С 1= Asin и С 2=А cos , то получим или (4. 5) Тогда При t=0 откуда График свободных колебаний, построенный по формуле (4. 5), изображен на рис. 4. 3. Величина , максимального отклонения от положения равновесия А называется амплитудой колебаний.

Рис. 4. 3. График свободных колебаний Время Т, за которое совершается одно колебание, называется периодом колебаний, величина a , характеризующая смещение синусоиды, называется начальной фазой колебаний, (kt+ a) - фазой колебаний, k- круговой (циклической) частотой колебаний. Последняя величина будет равна угловой скорости вращения отрезка, получающегося путем проектирования точек графика на окружность радиуса А. Круговая частота колебаний в общем случае находится по формуле , (4. 6)

где а и с соответственно коэффициенты инерции и жесткости системы, определяемые из выражений для кинетической и потенциальной энергии системы. За одно колебание фаза колебаний изменяется на угол 2 , то есть. тсюда можно найти связь между периодом и круговой частотой (4. 7) На основании полученных формул можно сделать выводы о свойствах свободных колебаний системы с одной степенью свободы. 1. Свободные колебания системы представляют собой гармонические колебания. 2. Амплитуды колебаний точек системы , а также начальная фаза колебаний зависят от начальных условий.

3. Период и частота колебаний не зависят от начальных условий, а определяются свойствами самой системы, и для их нахождения не требуется решать дифференциальные уравнения. 4. Отношения амплитуд различных точек системы не зависят от начальных условий. Эти свойства свободных колебаний системы с одной степени свободы основываются на приближенных линейных дифференциальных уравнениях. Эти уравнения имеют достаточную точность лишь при малых амплитудах.

Крутильные колебания • Крутильными называются колебания, приводящие к изменению угла поворота. Крутильной жесткостью (жесткостью на кручение) называется момент, необходимый для вызывания угла закручивания, равного одному радиану. Размерность крутильной жесткости С – НМ. • Для круглого вала диаметром d и длиной L это значение находится из известной в сопротивлении материалов формулы где G модуль сдвига (модуль упругости второго рода).

Свободные колебания системы с одной степенью свободы при наличии сил вязкого сопротивления • Во многих случаях силы сопротивления , действующие на точки системы, пропорциональны скоростям этих точек • Где коэффициент пропорциональности. • При этом происходит уменьшение кинетической энергии системы (рассеивание, диссипация). • Вычислим обобщенные силы сопротивления для обобщенных координат qi ( i=1, . 2, …, S) , где S – число степеней свободы. • Так как , то

подставляя в обобщенные силы сопротивления получаем Аналогично находятся и другие обобщенные силы сопротивления. По аналогии с кинетической и потенциальной энергиями системы вводится понятие диссипативной функции или ; функции рассеивания Рэлея , где коэффициент пропорциональности ( аналог массы ). Тогда обобщенные силы сопротивления найдутся по формула

то есть их можно найти как частные производные от диссипативной функции по соответствующей обобщенной скорости, взятые с противоположным знаком. В случае стационарной связи диссипативную функцию можно представить в виде однородной положительной квадратичной функции обобщенной координаты или в общем виде , где коэффициент диссипации. Для системы с одной степенью свободы Для получения дифференциального уравнения воспользуемся уравнением Лагранжа второго рода .

где обобщенная сила для всех потенциальных си обобщенная сила сопротивления. Так как Подставляя эти значения в уравнение Лагранжа, получим или Введя обозначения получим (4. 8) Уравнение (4. 8) называется дифференциальным уравнением свободных колебаний при наличии сил

Решение этого уравнения зависит от соотношения коэффициента n, характеризующего сопротивление, и k собственной частоты колебаний, зависящей от инерционных и жесткостных характеристик системы. Рассмотрим три случая: 1. Случай малого сопротивления: n<k, Решение уравнения имеет вид (4. 9) Где , а значения постоянных А и зависят от начальных условий и равны Колебания, проходящие по закону (4. 9), называются затухающими. График затухающих колебаний изображен на рис. 4. 6.

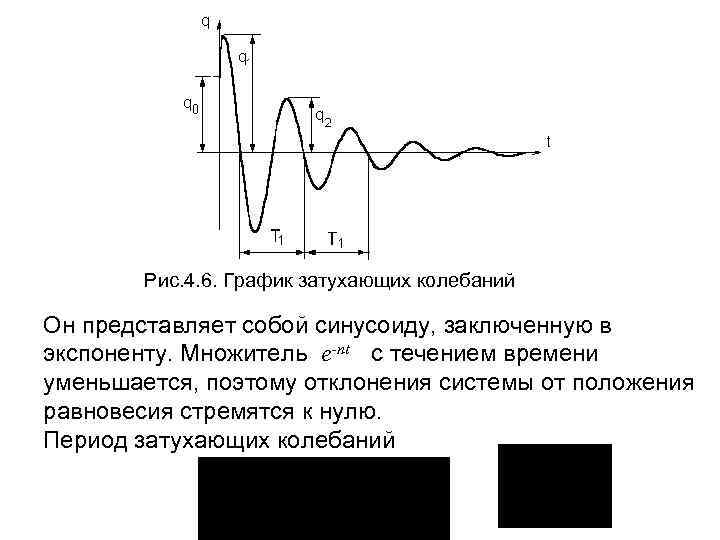
Рис. 4. 6. График затухающих колебаний Он представляет собой синусоиду, заключенную в экспоненту. Множитель e-nt c течением времени уменьшается, поэтому отклонения системы от положения равновесия стремятся к нулю. Период затухающих колебаний

где T=2 /k – период собственных колебаний. Из формулы (4. 9) видно, что период затухающих колебаний будет несколько больше периода собственных колебаний, но при малых значениях n эти величины приближенно равны, то есть малое сопротивление на период колебаний практически не влияет. Степень затухания характеризуется отношением двух последовательных отклонений отсюда Данная величина называется декрементом затухания. Модуль логарифма этой величины называется логарифмическим декрементом затухания.

2. Случай большого сопротивления: n>k, в этом случае решение уравнения (4. 8) ищется в виде где Эта функция монотонно убывает, и значение q стремится к 0. Данный вид движения называется апериодическим и не является колебательным. Вид этого движения зависит от начальных условий и показан на рис. 4. 7. В зависимости от начальных условий q 0 и движение будет иметь форму графиков 1, 2 или 3.

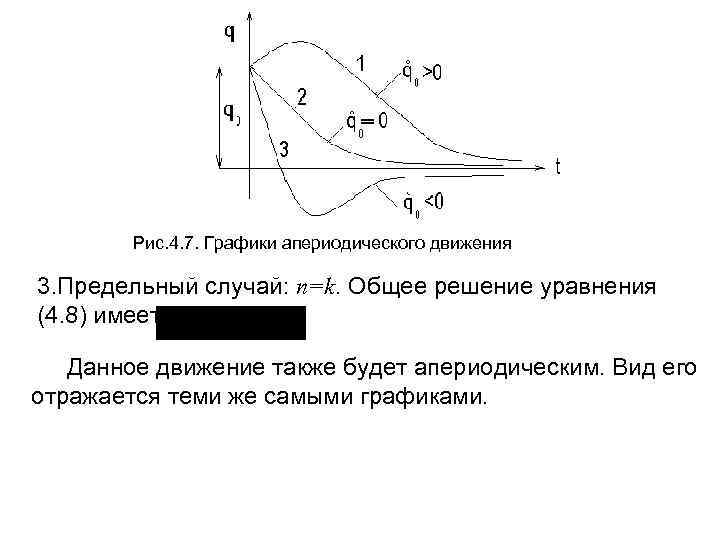
Рис. 4. 7. Графики апериодического движения 3. Предельный случай: n=k. Общее решение уравнения (4. 8) имеет вид Данное движение также будет апериодическим. Вид его отражается теми же самыми графиками.

Рассмотрев влияние сил сопротивления, пропорциональных скорости, можно сделать следующие выводы. 1. Силы сопротивления, совершая отрицательную работу, вызывают непрерывное уменьшение энергии вибрирующей системы, а следовательно, постепенное уменьшение амплитуд свободных колебаний. 2. Влияния малого сопротивления на частоту и период свободных колебаний системы незначительны, однако даже очень малое сопротивление вызывает быстрое затухание этих колебаний. 3. При больших сопротивлениях происходит апериодическое движение, то есть колебательный процесс отсутствует.

Свободные колебания при наличии сухого трения В случае нелинейного сопротивления обобщенная сила сопротивления является нелинейной функцией обобщенной скорости Дифференциальное уравнение свободных колебаний системы примет вид Точное решение данного уравнения при помощи элементарных функций в большинстве случаев невозможно, и, как правило, они решаются численными методами на ЭВМ.

Однако малое сопротивление, как линейное, так и нелинейное, влияет на частоту свободных колебаний незначительно, поэтому период колебаний можно принять равным периоду свободных колебаний, то есть Т=2 /к. Интерес представляет решение в случае действия на точки системы сил сухого (Кулонова) трения. В этом случае по модулю сила трения постоянна и определяется формулой Fтр = f N. Сила трения направлена в противоположную сторону скорости. График этой силы показан на рисунке (4. 9). В данном случае уравнение колебаний примет вид где QR- постоянная величина.

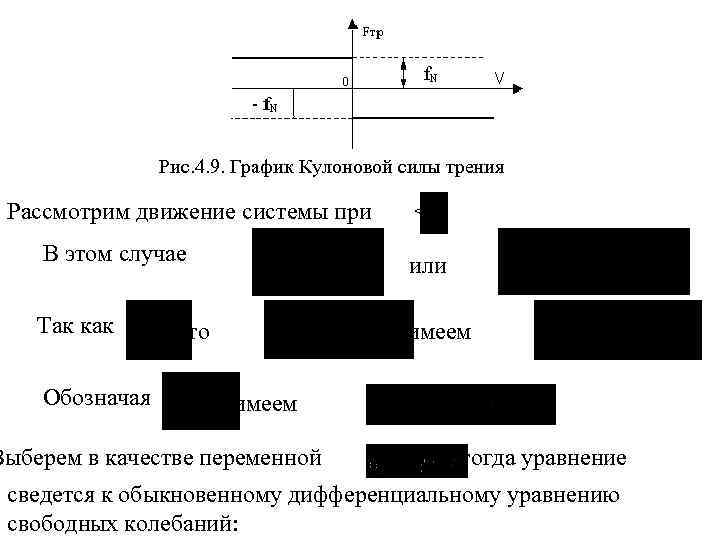
Рис. 4. 9. График Кулоновой силы трения Рассмотрим движение системы при <0. В этом случае или Так как , то имеем Обозначая имеем Выберем в качестве переменной , тогда уравнение сведется к обыкновенному дифференциальному уравнению свободных колебаний:

Если взять , то решение этого уравнения имеет вид За ту половину цикла колебаний, при которых <0 , величина q уменьшится на величину 2 а. Рассматривая вторую половину цикла, можно сделать вывод, что и за это время размахи величины q уменьшатся на 2 а, то есть амплитуда колебаний уменьшается в арифметической прогрессии. График этих колебаний изображен на рисунке 4. 10. Движение прекратится, если размахи колебаний становятся меньше а, так как в этом случае силы трения уравновешивают восстанавливающие силы

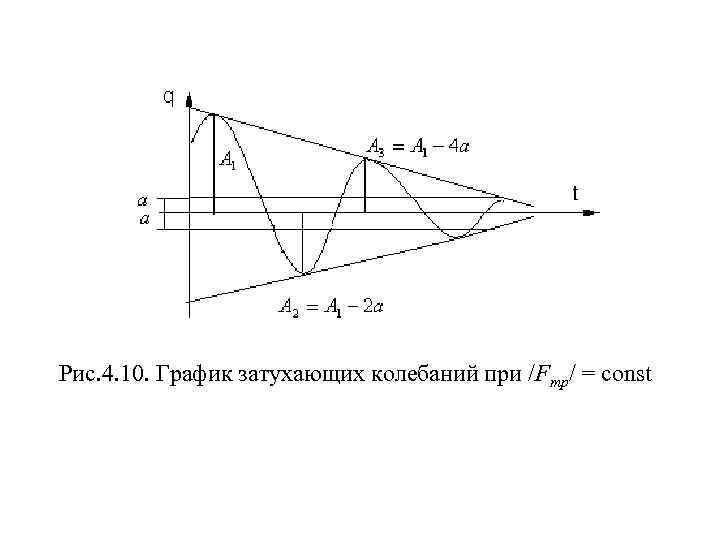
Рис. 4. 10. График затухающих колебаний при /Fтр/ = const

Вынужденные колебания системы с 1 степенью свободы Для поддержания колебательного процесса к системе прикладываются возбуждающие силы. При отсутствии сил сопротивления уравнение Лагранжа для рассматриваемой системы имеет вид где - обобщенная восстанавливающая сила, - обобщенная возбуждающая сила.

Так как для системы с 1 степенью свободы то, подставив в уравнение Лагранжа, получим (4. 11) где Это уравнение является общим дифференциальным уравнением вынужденных колебаний механической системы с 1 степенью свободы при отсутствии сил сопротивления. , Простейший случай, когда вынуждающая сила меняется по гармоническому закону Уравнение (4. 11) в этом случае примет вид

где р – частота вынуждающей силы. Это уравнение можно представить в виде (4. 12) Решение его ищется в виде где здесь - общее решение однородного уравнения Оно ищется в виде или где С 1, С 2, A и зависят от начальных условий. откуда частное решение, вид которого зависит от вида правой части, решение его ищется в виде Подставляя в уравнение (4. 12), получим

(4. 13) Таким образом Как видим, результирующее движение представляет собой сумму двух колебательных движений с частотами k и p. Представим дифференциальное уравнение в виде (4. 14) Продифференцировав по времени, получим (4. 15) Возьмем (тогда колебания вызываются возбуждающей силой).

Подставив начальные условия в уравнения (4. 14) и (4. 15) получим: или (4. 16) В случае, если p=k , то правая часть уравнения обращается в неопределенность 0/0 ( ). В этом случае частное решение вынужденных колебаний имеет вид тогда . При подстановке в дифференциальное уравнение, учитывая, что р=k получим

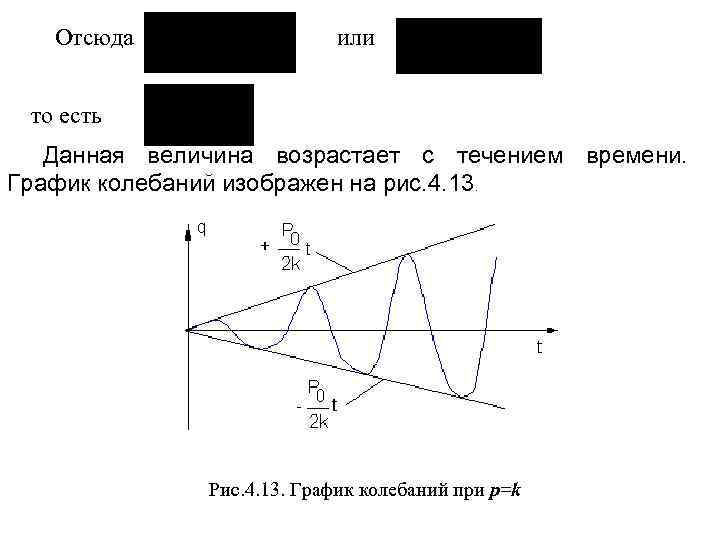
Отсюда или то есть Данная величина возрастает с течением времени. График колебаний изображен на рис. 4. 13. Рис. 4. 13. График колебаний при р=k

При p=k амплитуда вынужденных колебаний при изменении времени неограниченно возрастает (данное явление называется резонанс). Представим амплитуду вынужденных колебаний в виде Обозначим статическое отклонение системы от положения равновесия Тогда

Скачать презентацию ВВЕДЕНИЕ В ТЕОРИЮ КОЛЕБАНИЙ Примем в качестве общего

колебания 1ст.ppt

Количество слайдов: 79