Введение в прикладную статистику процессов На примере процесса

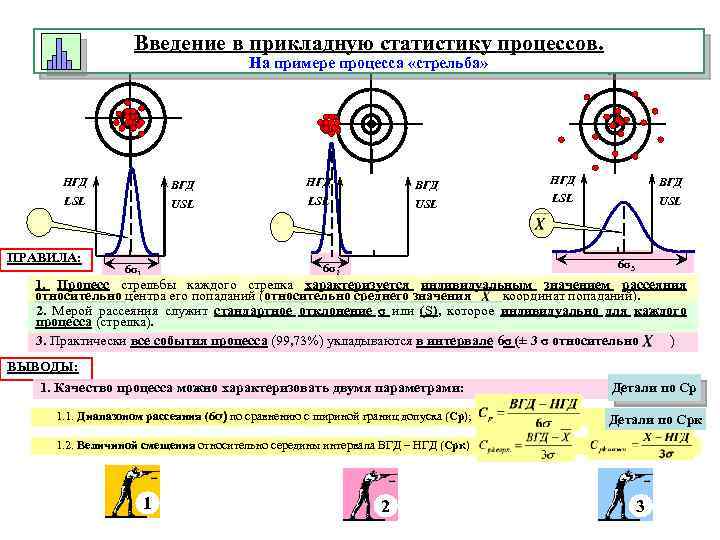Введение в прикладную статистику процессов. На примере процесса «стрельба» НГД ВГД LSL USL ПРАВИЛА: ВГД LSL USL 6σ3 6σ2 6σ1 НГД 1. Процесс стрельбы каждого стрелка характеризуется индивидуальным значением рассеяния относительно центра его попаданий (относительно среднего значения координат попаданий). 2. Мерой рассеяния служит стандартное отклонение σ или (S), которое индивидуально для каждого процесса (стрелка). 3. Практически все события процесса (99, 73%) укладываются в интервале 6σ (± 3 σ относительно ) ВЫВОДЫ: 1. Качество процесса можно характеризовать двумя параметрами: 1. 1. Диапазоном рассеяния (6σ) по сравнению с шириной границ допуска (Ср); Детали по Срк 1. 2. Величиной смещения относительно середины интервала ВГД – НГД (Срк) 1 2 3

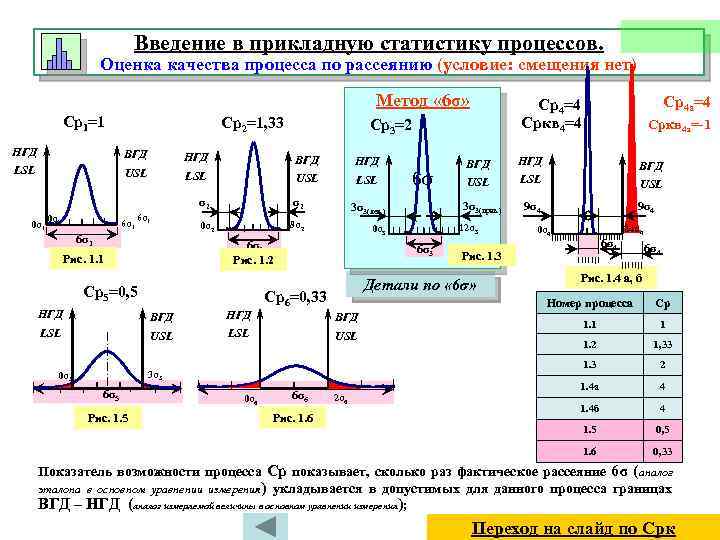Введение в прикладную статистику процессов. Оценка качества процесса по рассеянию (условие: смещения нет) Метод « 6σ» Ср1=1 Ср2=1, 33 Ср3=2 НГД ВГД НГД LSL ВГД USL НГД LSL USL LSL σ2 0σ1 6σ1 6σ1 σ2 3σ3(лев. ) 0σ2 8σ2 0σ3 6σ2 Рис. 1. 1 6σ Ср5=0, 5 НГД ВГД USL LSL USL 12σ3 9σ4 0σ4 6σ4 Рис. 1. 3 Детали по « 6σ» Ср6=0, 33 Сркв 4 а=-1 ВГД 3σ3(прав. ) 6σ3 Ср4 а=4 Ср4=4 Сркв 4=4 24σ4 6σ4 Рис. 1. 4 а, б USL LSL ВГД USL 3σ5 0σ5 6σ5 Рис. 1. 5 0σ6 6σ6 Рис. 1. 6 2σ6 Ср 1. 1 1 1. 2 1, 33 1. 3 ВГД Номер процесса 2 1. 4 а 4 1. 4 б 4 1. 5 0, 5 1. 6 НГД 0, 33 Показатель возможности процесса Ср показывает, сколько раз фактическое рассеяние 6σ (аналог эталона в основном уравнении измерения) укладывается в допустимых для данного процесса границах ВГД – НГД (аналог измеряемой величины в основном уравнении измерения ); Переход на слайд по Срк

Введение в прикладную статистику процессов. Выводы по связи качества процесса и значения Ср (рис. 2. 1. 1 -2. 1. 6) 1. Показатель возможности процесса Ср характеризует только величину рассеяния в процессе и не зависит от смещения процесса (см. формулу 1). 2. Чем лучше процесс (чем меньше рассеяние), тем показатель Ср больше и наоборот (рис. 1. 1 -1. 4). 3. Если Ср процесса больше 1 или равен 1, то брак в процессе может быть, а может и не быть: в этом случае всё будет определяться величиной смещения процесса (рис. 1. 4 а, б). 4. Если Ср меньше 1, то брак в процессе будет всегда, независимо от величины смещения процесса (рис. 1. 5, 1. 6). 5. Если Ср меньше или равен 1, 33 (рис. 1. 2), то процесс рекомендуется остановить (если это позволяют условия процесса), поскольку в этой ситуации в процессе возможен брак, и устранить причину увеличившегося рассеяния. 6. Показатель Ср не может принимать значения ≤ 0 (см. формулу 1). ГОСТ Р 50779. 44 -2001

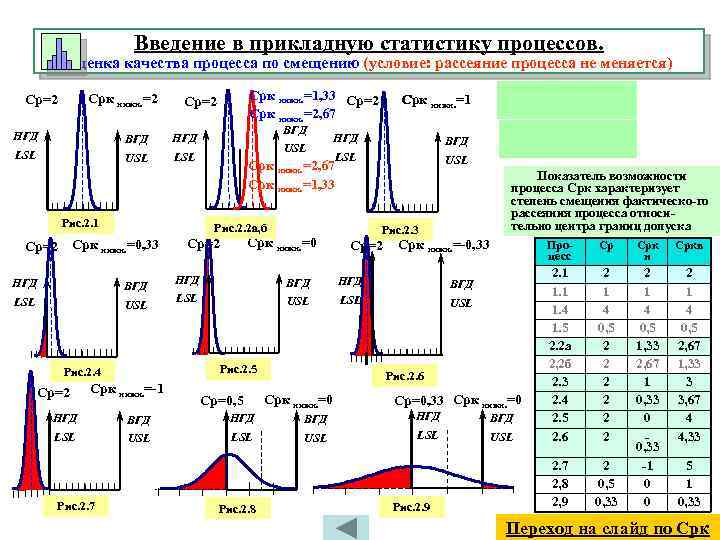Введение в прикладную статистику процессов. Оценка качества процесса по смещению (условие: рассеяние процесса не меняется) Срк нижн. =2 Срк нижн. =1, 33 Ср=2 Срк нижн. =2, 67 Ср=2 НГД ВГД LSL USL ВГД НГД LSL Рис. 2. 1 НГД ВГД LSL USL Срк нижн. =2, 67 Срк нижн. =1, 33 Рис. 2. 2 а, б Ср=2 Срк нижн. =0, 33 НГД ВГД LSL USL Срк нижн. =0 Ср=2 Срк нижн. =-1 Показатель возможности процесса Срк характеризует степень смещения фактическо-го рассеяния процесса относительно центра границ допуска Рис. 2. 3 Ср=2 Срк нижн. =-0, 33 НГД ВГД НГД LSL USL LSL Процесс USL Ср=0, 5 Рис. 2. 6 Срк нижн. =0 Ср=0, 33 Срк нижн. =0 НГД ВГД LSL USL Рис. 2. 7 Рис. 2. 8 Рис. 2. 9 Ср Срк н Сркв 2. 1 1. 4 1. 5 2. 2 а 2, 2 б 2. 3 2. 4 2. 5 2. 6 2 1 4 0, 5 2 2 2 2 0, 5 0, 33 2 1 4 0, 5 1, 33 2, 67 1 0, 33 0 0, 33 -1 0 0 2 1 4 0, 5 2, 67 1, 33 3 3, 67 4 4, 33 2. 7 2, 8 2, 9 ВГД Рис. 2. 5 Рис. 2. 4 Ср=2 USL Срк нижн. =1 5 1 0, 33 Переход на слайд по Срк

Введение в прикладную статистику процессов. Выводы по связи качества процесса и значения Срк (рис. 3. 1 -3. 9) 1. 2. 3. 4. 5. 6. 7. 8. 9. Показатели Сркн и Сркв характеризуют смещение процесса относительно центра границ допуска. Если в процессе нет смещения (процесс центросимметричен относительно границ допуска), то все три показателя (Ср, Сркн и Сркв) равны между собой (рис. 2. 1, 2. 1 2. 4 2. 5). При смещении процесса в сторону НГД, показатель Сркн уменьшается относительно значения Ср, а показатель Сркв – увеличивается на ту же величину (рис. 2. 2 а, 2. 3 -2. 7). При смещении в сторону ВГД уменьшается Сркв, а Сркн - увеличивается (рис. 2. 2 б). Если известен Ср и один из показателей Срк, то неизвестный показатель Срк можно вычислить по формуле 3, либо по правилу: «насколько один из показателей Срк уменьшился относительно значения Ср, настолько другой показатель Срк увеличился относительно Ср» (рис. 2. 3 -2. 7). Если показатель Сркн =1 или Сркв=1, то это означает, что смещение процесса достигло такой величины, при которой малейшее смещение в направлении данной границы допуска приведет к появлению брака в процессе (рис. 2. 1: на этом рисунке малейшее смещение в любом направлении приведен к появлению брака). Если один из показателей Срк меньше 1, то это означает, что по данной границе допуска имеет место брак (рис. 2. 4 -2. 7). Если оба показателя Сркн и Сркв меньше 1, то это означает, что брак есть как по нижней, так и по верхней границам допуска (рис. 1. 5, 1. 6, 2. 8 и 2. 9). Причем брака больше по той из границ допуска, по которой показатель Срк имеет наименьшее значение. Если один из показателей Срк=0, то это означает, что брак по данной границе допуска равен 50%, а в целом в процессе - 50% (если Ср ≥ 0, 5, рис. 2. 8) или больше 50%, но меньше 100%, если Ср < 0, 5 (рис. 2. 9). Если Срк меньше 0, то это означает, что брак по данной границе допуска больше 50% (рис. 2. 6 -2. 7). Если Срк меньше или равен -1, то это означает, что брак по данной границе допуска составляет 100% (рис. 2. 7). ГОСТ Р 50779. 44 -2001

Введение в прикладную статистику процессов. Примеры использования показателей Ср и Срк для анализа качества процессов

Введение в прикладную статистику процессов. Примеры использования показателей Ср и Срк для анализа качества процессов

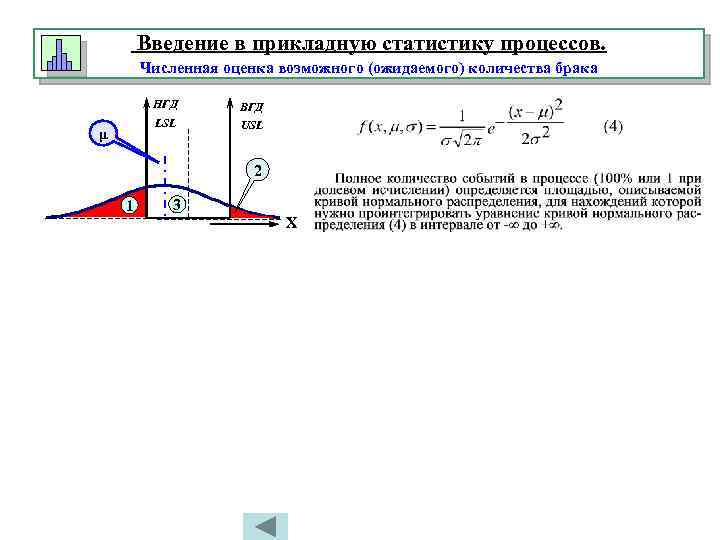Введение в прикладную статистику процессов. Численная оценка возможного (ожидаемого) количества брака НГД LSL μ ВГД USL 2 1 3 Х

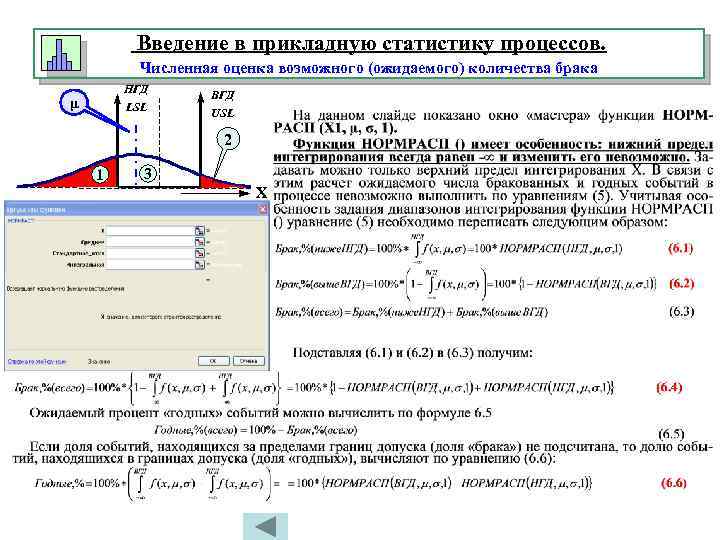Введение в прикладную статистику процессов. Численная оценка возможного (ожидаемого) количества брака НГД μ LSL ВГД USL 2 1 3 Х

Введение в прикладную статистику процессов. Численная оценка возможного (ожидаемого) количества брака В некоторых случаях в распоряжение специалиста, который по результатам статистического анализа параметров μ LSL USL процесса должен вычислить ожидаемое количество брака и годного продукта, передаются не результаты непосредственного 2 измерения параметров процесса, а уже вычисленные значения Ср и Срк. 3 1 В этом случае также можно применить функцию НОРМРАСП(), в аргументах которой будут использованы Х значения математического ожидания μ и стандартного отклонения σ, вычисленные на основе значений ВГД, НГД, Ср и Срк. Формулы для расчета ожидаемого количества брака с использованием функции НОРМРАСП() в этом случае будут иметь следующий вид: НГД ВГД

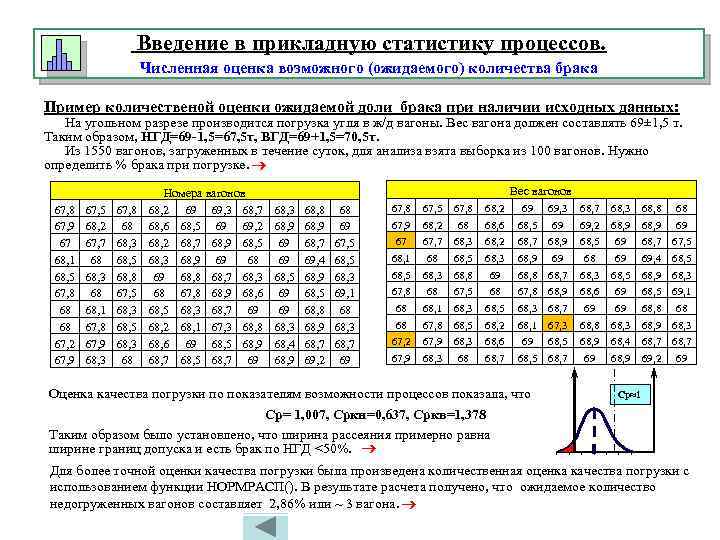Введение в прикладную статистику процессов. Численная оценка возможного (ожидаемого) количества брака Пример количественой оценки ожидаемой доли брака при наличии исходных данных: На угольном разрезе производится погрузка угля в ж/д вагоны. Вес вагона должен составлять 69± 1, 5 т. Таким образом, НГД=69 -1, 5=67, 5 т, ВГД=69+1, 5=70, 5 т. Из 1550 вагонов, загруженных в течение суток, для анализа взята выборка из 100 вагонов. Нужно определить % брака при погрузке. 67, 8 67, 9 67 68, 1 68, 5 67, 8 68 68 67, 2 67, 9 67, 5 68, 2 67, 7 68 68, 3 68 68, 1 67, 8 67, 9 68, 3 67, 8 68 68, 3 68, 5 68, 8 67, 5 68, 3 68 Номера вагонов 68, 2 69 69, 3 68, 7 68, 6 68, 5 69 69, 2 68, 7 68, 9 68, 5 68, 3 68, 9 69 68, 8 68, 7 68, 3 68 67, 8 68, 9 68, 6 68, 5 68, 3 68, 7 69 68, 2 68, 1 67, 3 68, 8 68, 6 69 68, 5 68, 9 68, 7 68, 5 68, 7 69 Вес вагонов 68, 3 68, 9 69 69 68, 5 69 69 68, 3 68, 4 68, 9 68, 8 68, 9 68, 7 69, 4 68, 9 68, 5 68, 8 68, 9 68, 7 69, 2 68 69 67, 5 68, 3 69, 1 68 68, 3 68, 7 69 67, 8 67, 5 67, 8 68, 2 69 69, 3 68, 7 68, 3 68, 8 68 67, 9 68, 2 68 68, 6 68, 5 69 69, 2 68, 9 69 67 67, 7 68, 3 68, 2 68, 7 68, 9 68, 5 69 68, 7 67, 5 68, 1 68 68, 5 68, 3 68, 9 69 68 69 69, 4 68, 5 68, 3 68, 8 69 68, 8 68, 7 68, 3 68, 5 68, 9 68, 3 67, 8 68 67, 5 68 67, 8 68, 9 68, 6 69 68, 5 69, 1 68 68, 1 68, 3 68, 5 68, 3 68, 7 69 69 68, 8 68 68 67, 8 68, 5 68, 2 68, 1 67, 3 68, 8 68, 3 68, 9 68, 3 67, 2 67, 9 68, 3 68, 6 69 68, 5 68, 9 68, 4 68, 7 67, 9 68, 3 68 68, 7 68, 5 68, 7 69 68, 9 69, 2 69 Оценка качества погрузки по показателям возможности процессов показала, что Ср= 1, 007, Сркн=0, 637, Сркв=1, 378 Таким образом было установлено, что ширина рассеяния примерно равна ширине границ допуска и есть брак по НГД <50%. Ср≈1 Для более точной оценки качества погрузки была произведена количественная оценка качества погрузки с использованием функции НОРМРАСП(). В результате расчета получено, что ожидаемое количество недогруженных вагонов составляет 2, 86% или 3 вагона.

Введение в прикладную статистику процессов. Пример расчета возможного (ожидаемого) количества брака μ ВГД LSL 1 а НГД USL 2 1 Х

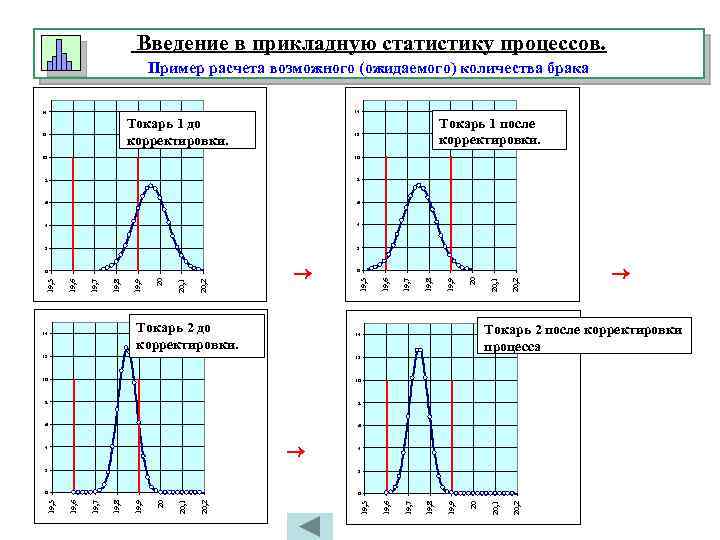Введение в прикладную статистику процессов. Пример расчета возможного (ожидаемого) количества брака 14 14 Токарь 1 до корректировки. 12 Токарь 1 после корректировки. 12 10 10 8 8 6 6 4 4 2 2 Токарь 2 до корректировки. 14 20, 2 20, 1 20 19, 9 19, 8 19, 7 0 19, 6 19, 5 20, 2 20, 1 20 19, 9 19, 8 19, 7 19, 6 19, 5 0 Токарь 2 после корректировки процесса 14 12 12 10 10 8 8 6 6 4 4 20, 2 20, 1 20 19, 9 19, 8 19, 7 19, 6 19, 5 20, 2 20, 1 20 19, 9 0 19, 8 0 19, 7 2 19, 6 2 19, 5

Введение в прикладную статистику процессов. Спасибо за внимание.

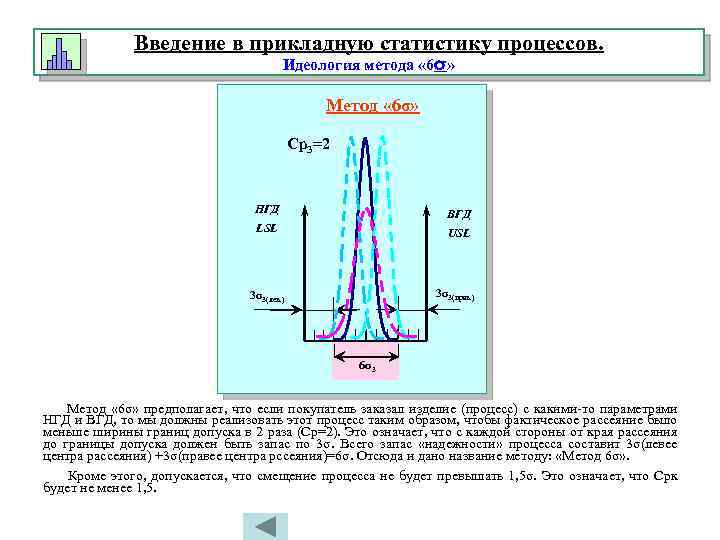Введение в прикладную статистику процессов. Идеология метода « 6σ» Метод « 6σ» Ср3=2 НГД ВГД LSL USL 3σ3(прав. ) 3σ3(лев. ) 6σ3 Метод « 6σ» предполагает, что если покупатель заказал изделие (процесс) с какими-то параметрами НГД и ВГД, то мы должны реализовать этот процесс таким образом, чтобы фактическое рассеяние было меньше ширины границ допуска в 2 раза (Ср=2). Это означает, что с каждой стороны от края рассеяния до границы допуска должен быть запас по 3σ. Всего запас «надежности» процесса составит 3σ(левее центра рассеяния) +3σ(правее центра рссеяния)=6σ. Отсюда и дано название методу: «Метод 6σ» . Кроме этого, допускается, что смещение процесса не будет превышать 1, 5σ. Это означает, что Срк будет не менее 1, 5.

Введение в прикладную статистику процессов. Примеры использования показателей Ср и Срк для анализа качества процессов

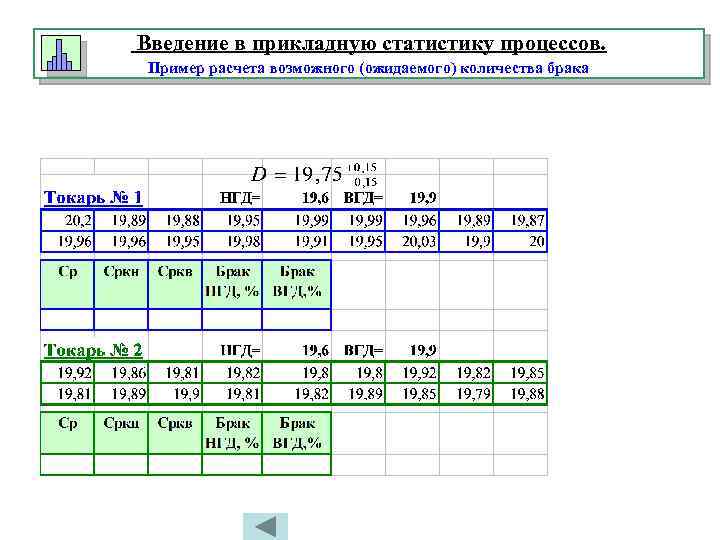Введение в прикладную статистику процессов. Пример расчета возможного (ожидаемого) количества брака