ВВЕДЕНИЕ В ФИЗИКУ И МОДЕЛИРОВАНИЕ ФОТОННЫХ КРИСТАЛЛОВ Лекция

ВВЕДЕНИЕ В ФИЗИКУ И МОДЕЛИРОВАНИЕ ФОТОННЫХ КРИСТАЛЛОВ Лекция 4 2013

Волны в диэлектрических средах В диэлектрическом носителе ненулевая поляризация P вызвана внешним электрическим полем E. Чтобы понять физическое значение P, будем предполагать, что среда содержит положительные и отрицательные заряды (например, протоны и электроны). Когда электрическое поле присутствует, оно разделяет положительные и отрицательные заряды. Это разделение заряда создает дополнительное электрическое поле. Это дополнительное электрическое поле называют наведенной поляризацией. Если среда линейна и изотропна, P линейно пропорционален E и может быть выражена как где называют электрической восприимчивостью. Линейная восприимчивость – в общем случае, тензор второго ранга, но сводится к скаляру для изотропной среды, например, для кварцевого стекла

В общем случае, восприимчивость – функция частоты примененного поля. Когда поле E(t) – произвольная функция времени t, поляризация – свертка преобразования Фурье ( ) с E(t). Это отражает факт, что диполи в материале не могут мгновенно ответить на приложенное поле, и соображения причинной связи приводят к соотношениям Кармерса-Кронига. D - диэлектрическое смещение - диэлектрической постоянной или относительной диэлектрической проницаемостью диэлектрика Диэлектрическая постоянная материала оказывает воздействие на перемещение через материал электромагнитных сигналов (свет, миллиметровые волны, и т. д. ). Высокое значение диэлектрической постоянной делает пространственный интервал для ЭМВ в материале как бы больше. Это означает, что свет перемещается более медленно. Происходит сжатие волны, как будто сигнал имеет более короткую длину волны.

Показатель преломления диэлектрической среды Для электромагнитного поля в диэлектрической среде без тока из уравнении путем исключения H (аналогично преобразованиям сделанным ранее для вакуума), получим Скорость распространения волн по сравнению с вакуумом изменяется с c на c/n, где является показателем преломления среды. Следовательно, показатель преломления среды – мера того, с какой скоростью свет (или другие волны) приходит в среде.

Диэлектрическая среда с потерями В волновое уравнение может быть включен ток, чтобы учесть потери мощности во время распространения волн. В этом случае, индуцированный ток связан с электрическим полем J = E , где - проводимость. Если электрическое поле зависит от времени по закону ej t, то плотность индуцированного тока имеет ту же самую временную зависимость. Поэтому, эффект появления тока включается в электрическую восприимчивость следующим образом. Из правой части одного из исходных уравнений Максвелла где (r, ) - диэлектрическая постоянная, которая в общем случае является комплексной величиной.

Вещественные и мнимые части (r, ) соответствуют показателю преломления n и коэффициенту поглощения по определению и связанные электрической восприимчивостью Величины n и зависят от частоты. Мнимая часть показателя преломления представляет собой потери (если она - отрицательная величина) или усиление (если - положительная). Частотная зависимость n известна как хроматическая дисперсия. В случае потерь, существующих в среде, излучение по экспоненте затухает, как показано на рисунке.

Если подставить в то волновое уравнение для электрического поля сводится к: Используя преобразование Фурье для E(r, t) по формуле и используя подобные преобразования для P(r, t), можно записать волновое уравнение в частотном представлении с частотно-зависимой диэлектрической постоянной и (r, ) является временным преобразованием Фурье (r, t).

В представлении частот волновое уравнение имеет вид для свободного пространства волновое число k 0 определено как и 0 - длина волны оптического поля, осциллирующего с частотой в вакууме. Решая уравнение, получают оптические моды.

Групповая скорость Существует определение двух различных скоростей: групповой скорости и фазовой скорости. Рассмотрим бегущую волну в следующей форме: Преобразование Фурье относительно времени дает Эту волну постоянной частоты называют монохроматической, она – незатухающая. Фазовая скорость – скорость плоскости постоянной фазовой, которая перемещается в направление распространения.

Для рассматриваемой плоской волны ее амплитуда или энергия, являются постоянными по всему пространству. Переменные: время и положение – независимы. Другими словами, нельзя сказать: "где" волна. Фактически, она всюду. С другой стороны, две плоские волны, имеющие небольшую разность частот и волнового числа, или Огибающая объединенной волны имеет скорость называется групповой скоростью, которую связывают со скоростью распространения энергии.

Понятие групповой скорости может быть обобщено от случая двух монохроматических волн до случая "волнового пакета". Волновой пакет или его амплитуда перемещаются с групповой скорости vg. а) если нет дисперсии (это справедливо для вакуума) и для веществ с n > 1, и vгр ≠ vф; б) если – нормальная дисперсия, т. е. vгр < vф, в) если – аномальная дисперсия, т. е. vгр > vф. Вопросы: фазовая скорость, групповая скорость, скорость распространения энергии

Групповая скорость — это величина, характеризующая скорость распространения «группы волн» - то есть более или менее хорошо локализованной квазимонохроматической волны (волны с достаточно узким спектром). Обычно интерпретируется как скорость перемещения максимума амплитудной огибающей квазимонохроматического волнового пакета (или цуга волн). В случае рассмотрения распространения волн в пространстве размерностью больше единицы подразумевается как правило волновой пакет близкий по форме к плоской волне. Групповая скорость во многих важных случаях определяет скорость переноса энергии и информации квазисинусоидальной волной (хотя это утверждение в общем случае требует серьёзных уточнений и оговорок). Групповая скорость определяется динамикой физической системы, в которой распространяется волна (конкретной среды, конкретного поля и т. п. ). В большинстве случаев подразумевается линейность этой системы (точно или приближенно). Для одномерных волн групповая скорость вычисляется из закона дисперсии: , где — угловая частота, — волновое число.

Групповая скорость волн в пространстве (например, трехмерном или двумерном) определяется градиентом частоты по волновому вектору : • Замечание: групповая скорость вообще говоря зависит от волнового вектора (в одномерном случае - от волнового числа), то есть вообще говоря различна для разной величины и для разных направлений волнового вектора. Частные случаи В одномерных средах без дисперсии групповая скорость формально совпадает с фазовой скоростью лишь в случае одномерных волн. В диссипативных (поглощающих) средах групповая скорость уменьшается с увеличением частоты в случае нормальной дисперсии фазовой скорости и, наоборот, увеличивается в средах с аномальной дисперсией. Если дисперсионные свойства среды таковы, что волновой пакет распространяется в ней без существенных изменений формы своей огибающей, групповая скорость обычно может быть интерпретирована как скорость переноса «энергии» волны и скорость, с которой могут быть переданы с помощью волнового пакета сигналы, несущие информацию, (то есть «скорость распространения причинности» ).

Дисперсия водных волн (красные точки движутся со скоростью фазы, зелёные - с групповой скоростью). В данном случае фазовая скорость в два раза превышает групповую.

ИЗГОТОВЛЕНИЕ ФОТОННЫХ КРИСТАЛЛОВ 1. Метод коллоидной сборки. 2. Метод травления 3. Голографические методы 4. Другие методы

ОСНОВНЫЕ ПРИНЦИПЫ ВЫЧИСЛЕНИЯ ХАРАКТЕРИСТИК ФОТОННЫХ КРИСТАЛЛОВ

Вычисление распределения поля в одномерном (1 -D) фотонном кристалле Понимание физических параметров периодических структур может быть дано при рассмотрении и вычислении распределения поля в произвольной многослойной структуре, когда она облучается излучением одной длины волны. Произвольная многослойная структура обозначает структуру, содержащую много диэлектрических слоев с произвольными значениями толщины и диэлектрической постоянной. При этом в пределах одного слоя структура строго однородна. Ограничимся самым простым случаем изотропной и непроводящей среды. Предположим, что материал является немагнитным, его относительная проницаемость равна 1. Материальные уравнения для немагнитной среды принимают следующую форму: где 0 – магнитная константа или вакуумная проницаемость, и r и 0 – относительная диэлектрическая проницаемость и электрическая константа.

Выбранная форма пары уравнений записана для среды, на которую действует электрическое поле, но она невосприимчива к магнитному полю. В пределах данной модели не будут рассматриваться магнитные свойства среды и её анизотропия. Подставим материальные уравнения в уравнения Максвелла, чтобы получить систему без электрического смещения и магнитной проницаемости. Взяв ротор от первого уравнения, подставим второе уравнение в первое, получим следующее соотношение: Аналитическое решение такого нестационарного уравнения достаточно сложное.

В случае распространения излучения с постоянной амплитудой, нет никакой необходимости в решении неустановившегося уравнения. Чтобы упростить проблему, выведем уравнение Гельмгольца. Представим электрическое поле как произведение комплексной амплитуды и зависящей от времени гармонической функции: Уравнение Гельмгольца не содержит зависящие от времени функции. Решая это уравнение, можно найти коэффициент отражения и прозрачность конечной структуры, а также распределение поля и собственные частоты бесконечной структуры.

Рассмотрим конечную 1 -D многослойную структуру. Описание распространения излучения в такой структуре может быть найдено решением уравнения Гельмгольца, представленного в следующей форме: Рассматривается случай распространения света перпендикулярно к поверхности раздела от слоя к слою. У каждого уровня есть: • некоторая толщина (d 1, d 2. . . d. N-1) • показатель преломления (n 1, n 2. . . n. N). Структура окружена материалом с показателем преломления n 0 = n. N.

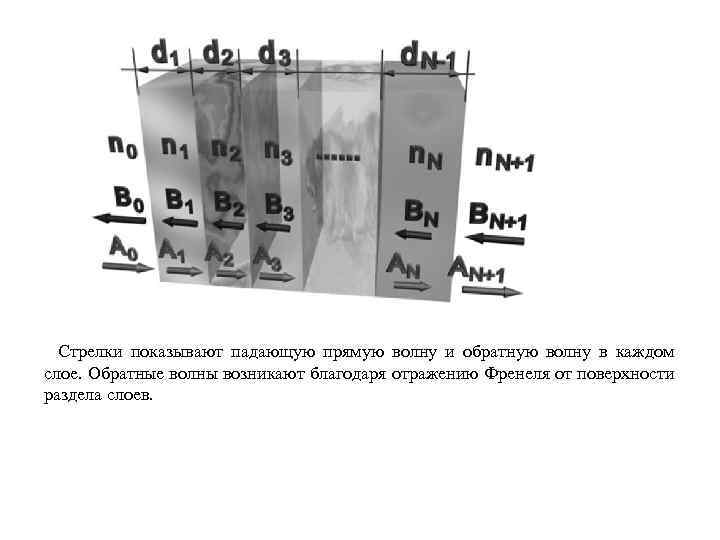Стрелки показывают падающую прямую волну и обратную волну в каждом слое. Обратные волны возникают благодаря отражению Френеля от поверхности раздела слоев.

Решение уравнения Гельмгольца для такой структуры состоит в определении амплитуд прямых и обратных волн в каждом слое. После этого возможно получение распределения поля в структуре так же, как определение коэффициента отражения и прозрачности структуры. Общее решение уравнения Гельмгольца для j уровня принимает следующую форму: где A и B – амплитуды прямых и обратных волн соответственно. Проходящие и отраженные волны существуют в каждом уровне. Их суперпозиция формирует распределение поля. Однако общего решения уравнения недостаточно, чтобы найти амплитуды волны. Для этого необходимо удовлетворить начальные и граничные условия. В нашем случае начальные условия определяет источник излучения. Если излучение попадает на структуру из свободного пространства, начальные условия определены на внешней границе области вычислений. Если источник света находится в структуре (например, активный слой), то начальные условия будут определены в соответствующем слое.

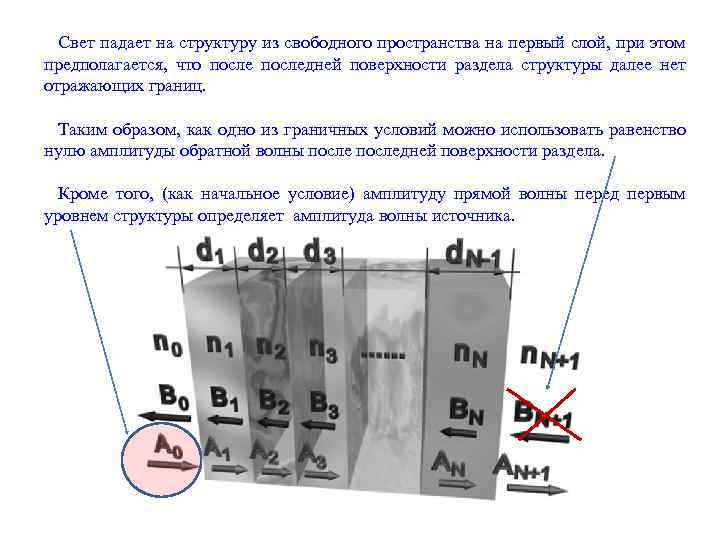Свет падает на структуру из свободного пространства на первый слой, при этом предполагается, что последней поверхности раздела структуры далее нет отражающих границ. Таким образом, как одно из граничных условий можно использовать равенство нулю амплитуды обратной волны последней поверхности раздела. Кроме того, (как начальное условие) амплитуду прямой волны перед первым уровнем структуры определяет амплитуда волны источника.

Граничных условий на внутренних поверхностях определяются распределением поля, т. е. "связью" на поверхностях раздела волновых функциями. В случае 1 -D многослойной структуры рассматривается только тангенциальная составляющая электрического поля, таким образом, граничные условия сформулированы как равенство волновых функций и их первых производных на поверхности раздела: Далее подставляем общее решение уравнений

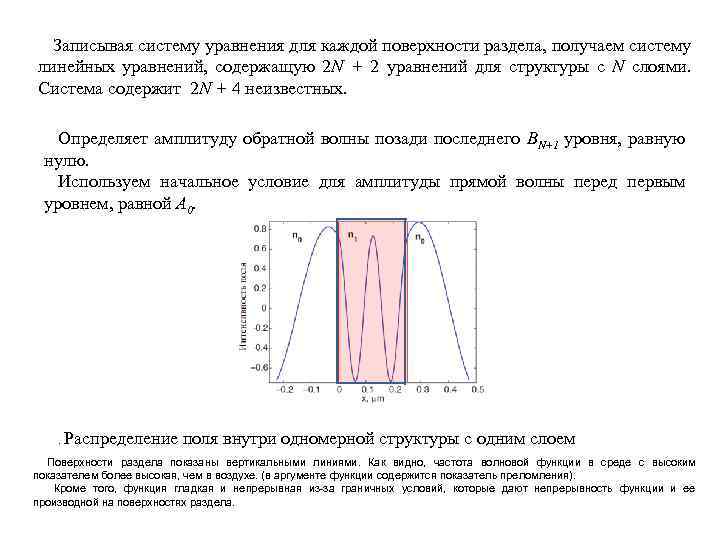Записывая систему уравнения для каждой поверхности раздела, получаем систему линейных уравнений, содержащую 2 N + 2 уравнений для структуры с N слоями. Система содержит 2 N + 4 неизвестных. Определяет амплитуду обратной волны позади последнего BN+1 уровня, равную нулю. Используем начальное условие для амплитуды прямой волны перед первым уровнем, равной A 0. Распределение поля внутри одномерной структуры с одним слоем . Поверхности раздела показаны вертикальными линиями. Как видно, частота волновой функции в среде с высоким показателем более высокая, чем в воздухе. (в аргументе функции содержится показатель преломления). Кроме того, функция гладкая и непрерывная из-за граничных условий, которые дают непрерывность функции и ее производной на поверхностях раздела.

Полученная линейная система уравнений решается стандартными методами, такими как метод Крамера. В результате решения получается ряд амплитуд прямых и обратных волн на каждом слое. Чтобы получить распределение поля в структуре, необходимо подставить амплитуды A и B в в общую форму решения. Делая это для каждого уровня, получим распределение электрического поля внутри 1 D многоуровневая структура.

метод Крамера Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно). Описание метода Для системы линейных уравнений с n неизвестными с определителем матрицы системы , отличным от нуля, решение записывается в виде i-ый столбец матрицы системы заменяется столбцом свободных членов.

Приложения вычисления распределения поля Предположим, что задана произвольная, но конечного размера периодическая структура; то есть, структура, где группа двух или большего числа слоев повторяется несколько раз. Поведение такой структуры довольно легко предсказать, если известны параметры ее слоев. Такая периодическая структура обычно упоминается как Брэгговская решетка или распределенный Брэгговский рефлектор. Особенность Брэгговской решетки - возможность варьировать прозрачность и спектр коэффициента отражения изменением параметров слоев. При этом у структуры очень высокий коэффициент отражения при некоторых определенных длинах волны, в то время как в других длинах волн она может быть прозрачна.

В случае структуры, содержащей периодически повторяемую пару уровней, длина волны с максимальным коэффициентом отражения, также известным как Брэгговская длина волны, может быть найдена из следующего уравнения: где na и da - показатель преломления и толщина первого уровня в паре, в nb и db - те же самые значения для второго уровня. Таким образом, Брэгговское условие удовлетворяется, если половина длины волны приравнивается к оптической толщине пары уровней. Условие для максимальной прозрачности соответствует выражению, похожему на (*), и имеет следующую форму: Уравнение показывает, что длина волны излучения должна быть равной оптической толщине пары уровней, чтобы удовлетворить условию максимальной прозрачности.

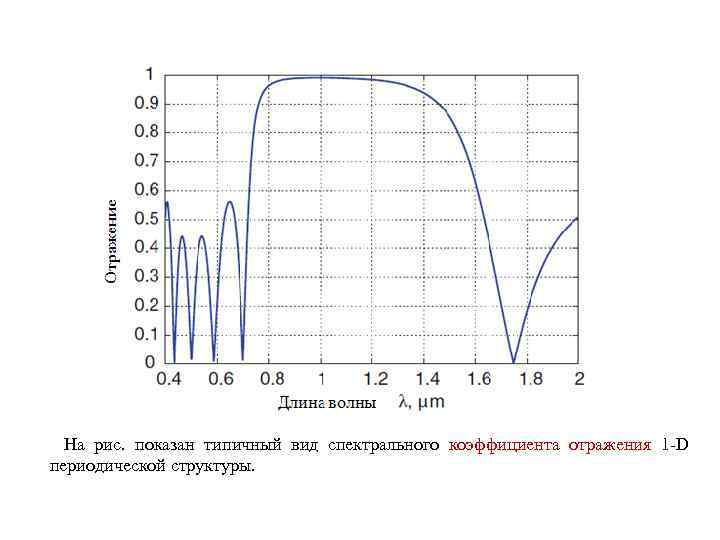На рис. показан типичный вид спектрального коэффициента отражения 1 -D периодической структуры.

Коэффициента отражения вычислен приведенной системы уравнений. численным решением выше Решение последовательно выполняется для различных длин волн; каждый раз получаем амплитуду обратных волн B 0 перед первым уровнем структуры. Поделив эту амплитуду на амплитуду падающей волны A 0 и возводя результат в квадрат, получим коэффициент отражения структуры на каждой длине волны. Как видно из рис. , коэффициент отражения резко зависит от длины волны. В данном расчете Брэгговская длина волны падает на значение длины волны равное 1. Это означает, что максимум коэффициента отражения наблюдается в этой длине волны.

Процесс вычисления, показанный выше, довольно легко понять и использовать. У него существует широкий диапазон приложений. Используя описанный метод возможно разработать различные пассивные оптические устройства, такие как рефлекторы с высоким к. п. д. , анти- отражательные фильтры, распределенные Брэгговские рефлекторы для вертикальной поверхности лазерного резонатора (VCSEL), мультиплексоры/демультиплексоры разделения по длинам волн на основе волоконной решетки Брэгга (FBG), зеркала перестраиваемых лазеров, и т. д.

Оптическая схема такого демультиплексора изображена на рисунке. . Демультиплексор на основе решетки Брэгга

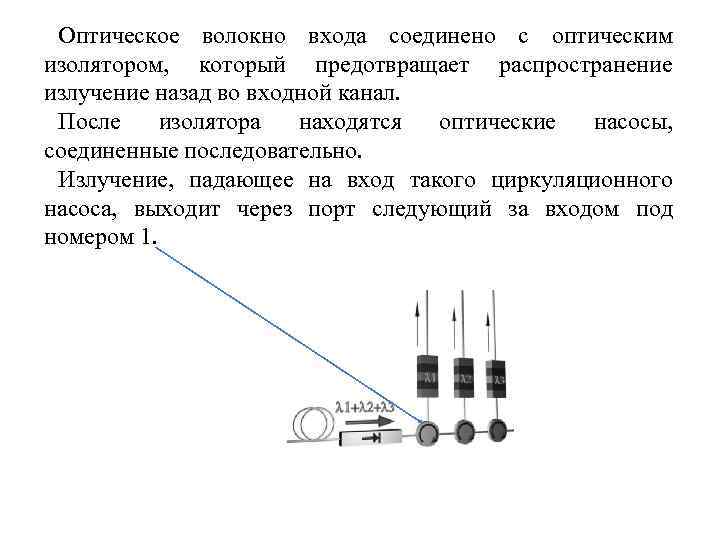Оптическое волокно входа соединено с оптическим изолятором, который предотвращает распространение излучение назад во входной канал. После изолятора находятся оптические насосы, соединенные последовательно. Излучение, падающее на вход такого циркуляционного насоса, выходит через порт следующий за входом под номером 1.

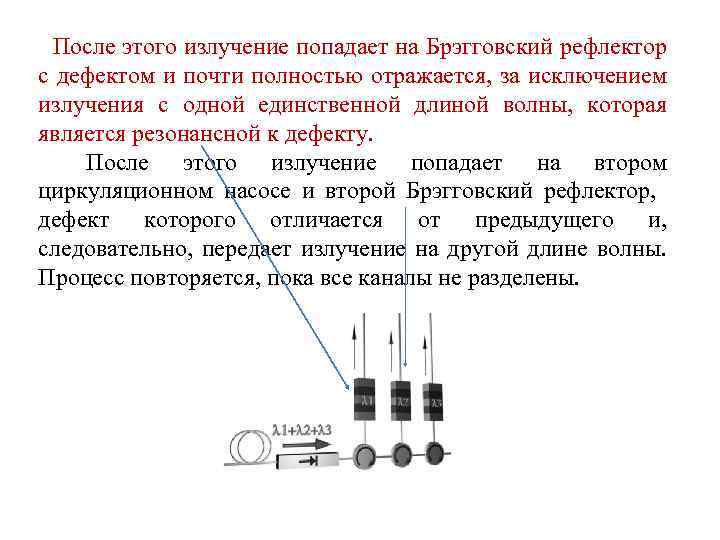После этого излучение попадает на Брэгговский рефлектор с дефектом и почти полностью отражается, за исключением излучения с одной единственной длиной волны, которая является резонансной к дефекту. После этого излучение попадает на втором циркуляционном насосе и второй Брэгговский рефлектор, дефект которого отличается от предыдущего и, следовательно, передает излучение на другой длине волны. Процесс повторяется, пока все каналы не разделены.

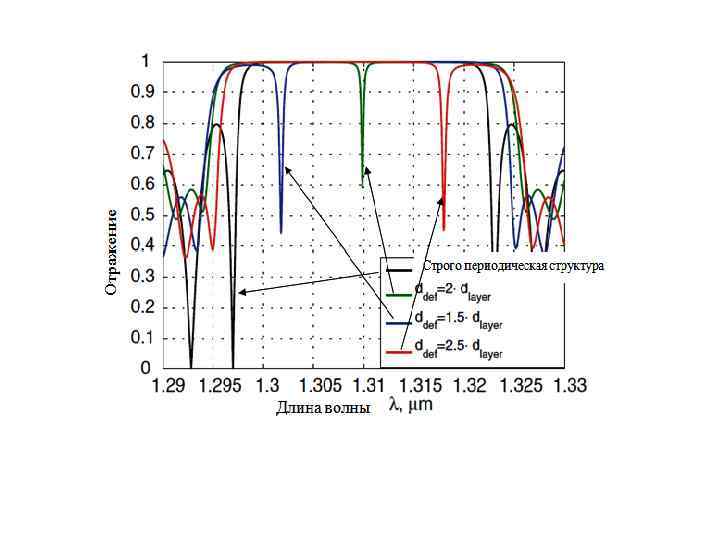
Основные элементы описанного демультиплексора - распределенные Брэгговские рефлекторы с дефектом, которые позволяют одной длине волны из широкого диапазона проходить, в то время как волны других длин отражаются. Рассмотрим подробно особенности этого проекта. Брэгговский рефлектор с дефектом представлен многослойной периодической структурой, в которой периодичность нарушена изменением некоторого параметра (показатель преломления или толщины) одного из слоев. Структура теперь представляет резонатор (дефектный уровень) с двумя зеркалами (распределенные Брэгговские рефлекторы от обеих сторон дефектного уровня). При этом изменяется спектр коэффициента отражения всей структуры. Если параметры дефектного уровня должным образом подобраны, резкий пик прозрачности появляется в пределах основного диапазона, где коэффициента отражения порядка единицы, как показано на рис. . Длина волны пика прозрачности соответствует резонансной длине волны дефекта.

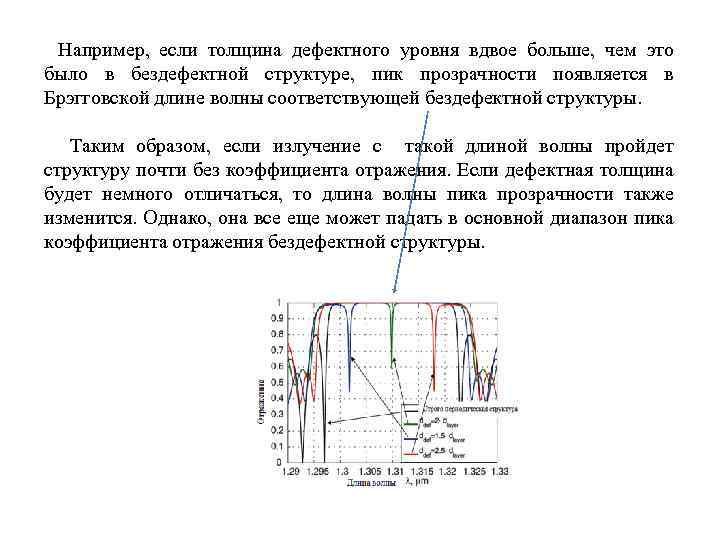Например, если толщина дефектного уровня вдвое больше, чем это было в бездефектной структуре, пик прозрачности появляется в Брэгговской длине волны соответствующей бездефектной структуры. Таким образом, если излучение с такой длиной волны пройдет структуру почти без коэффициента отражения. Если дефектная толщина будет немного отличаться, то длина волны пика прозрачности также изменится. Однако, она все еще может падать в основной диапазон пика коэффициента отражения бездефектной структуры.

Если первоначальный сигнал содержит много каналов на различных длинах волн, то попадая в Брэгговский рефлектор с дефектом, только один канал пройдет, в то время как другие будут отражены. Должным образом выбранная толщина дефектного уровня каждого рефлектора позволяет выполнять пространственное разделение всех каналов. Описанный метод позволяет автоматизировать такую процедуру и делает задачу просто технической.