ВВЕДЕНИЕ В АНАЛИЗ ФУНКЦИЯ Определения 2 1

ВВЕДЕНИЕ В АНАЛИЗ ФУНКЦИЯ

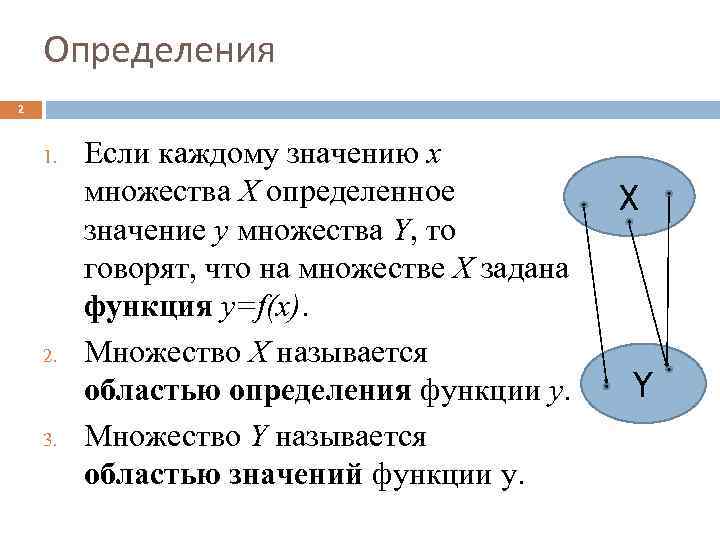Определения 2 1. 2. 3. Если каждому значению x множества X определенное значение y множества Y, то говорят, что на множестве X задана функция y=f(x). Множество X называется областью определения функции y. Множество Y называется областью значений функции y. X Y

Определения 3 4. Функция y=f(x) называется Y возрастающей на некотором промежутке множества X, если при y y x 1y 2. 6. Возрастающие и убывающие функции называются монотонными. 2 1 x 2 X 1 2 x 1 x 2 X

Определения 4 7. Функция y=f(x) называется неубывающей на некотором промежутке множества X, если при x 1

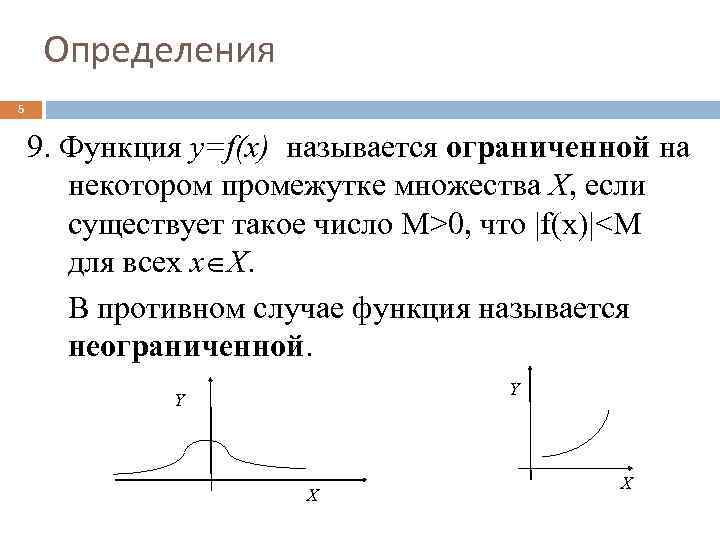Определения 5 9. Функция y=f(x) называется ограниченной на некотором промежутке множества X, если существует такое число M>0, что |f(x)|

Определения 6 10. Функция y=f(x) называется четной, если для любых значений x X f(- x)= f(x). 11. Функция y=f(x) называется нечетной, если для любых значений x X f(- x)= - f(x). 12. В остальных случаях y=f(x) функция общего вида. 13. Функция y=f(x) называется периодической с периодом T 0, если для любых значений x X f(x+T)= f(x).

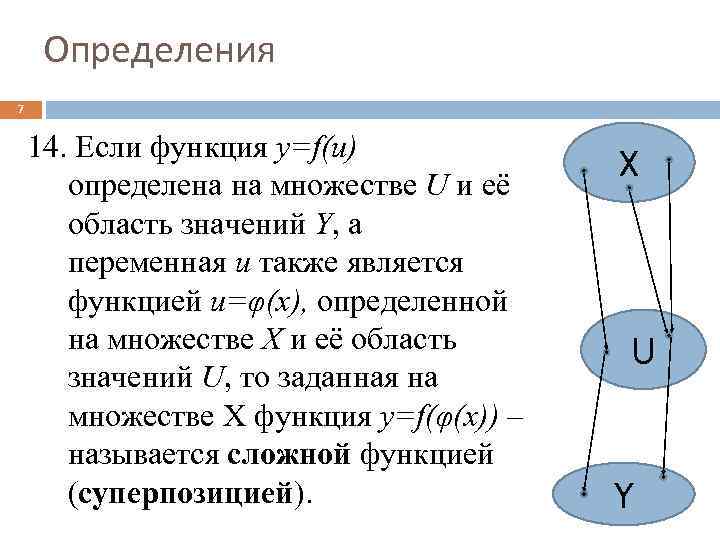Определения 7 14. Если функция y=f(u) определена на множестве U и её область значений Y, а переменная u также является функцией u=φ(x), определенной на множестве X и её область значений U, то заданная на множестве X функция y=f(φ(x)) – называется сложной функцией (суперпозицией). X U Y

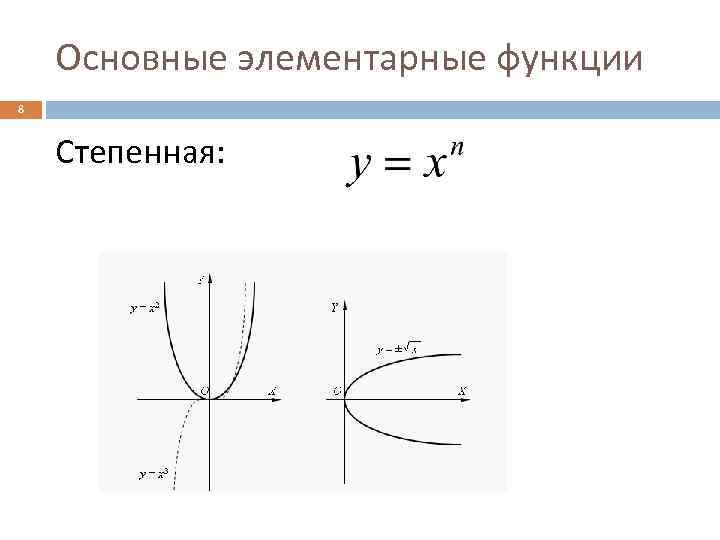Основные элементарные функции 8 Степенная:

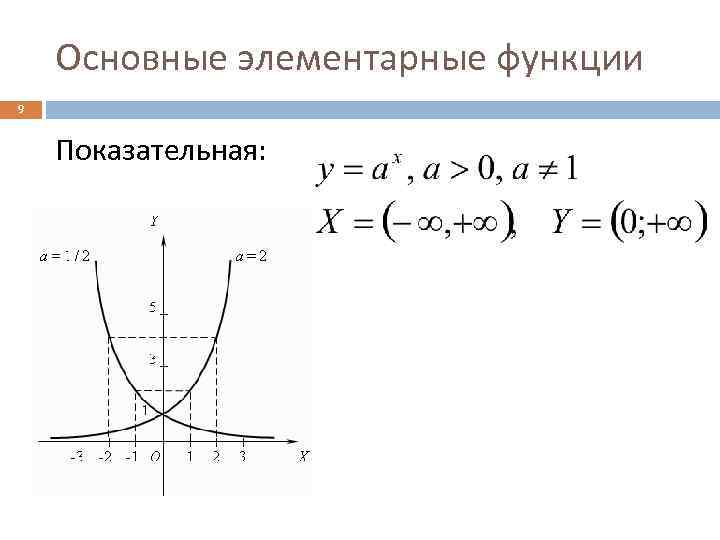Основные элементарные функции 9 Показательная:

Основные элементарные функции 10 Логарифмическая:

Основные элементарные функции 11 Тригонометрические:

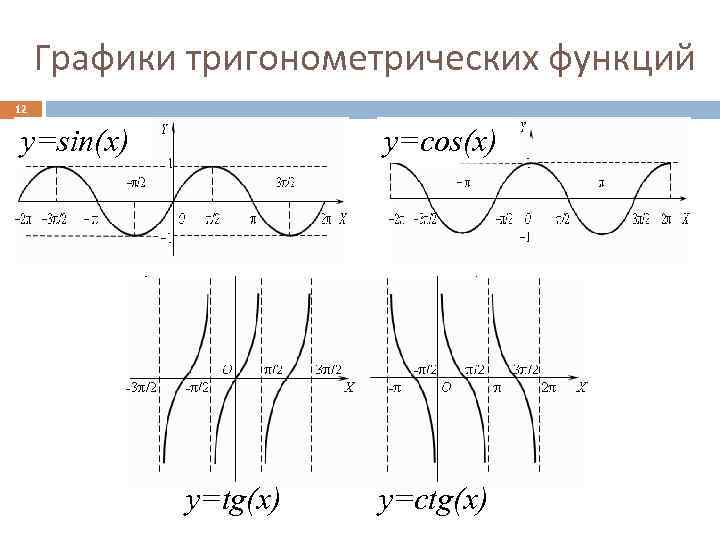Графики тригонометрических функций 12 y=sin(x) y=cos(x) y=tg(x) y=ctg(x)

Основные элементарные функции 13 Обратные тригонометрические:

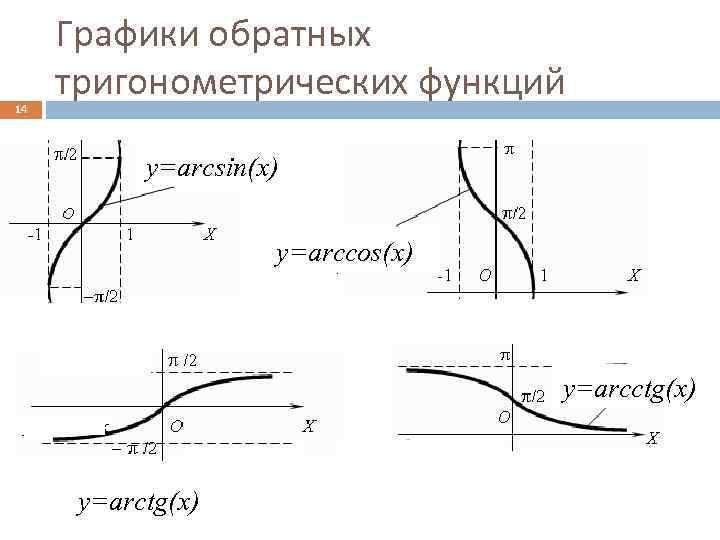14 Графики обратных тригонометрических функций y=arcsin(x) y=arccos(x) y=arcctg(x) y=arctg(x)

Обратные функции 15 Если функция y=f(x) определена на множестве X и имеет множество значений Y, и если для любых x 1, x 2 X из условия x 1 x 2 следует условие y(x 1) y(x 2), то каждому значению y Y можно поставить в соответствие определенное значение x X такое, что f(x)= y. Т. е. на множестве Y можно определить функцию x=g(y), называемую обратной к функции y=f(x)

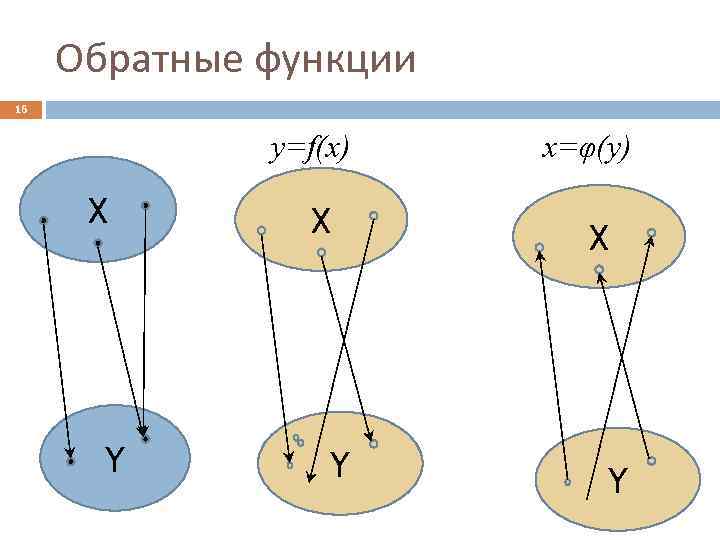Обратные функции 16 y=f(x) X Y x=φ(y) X Y

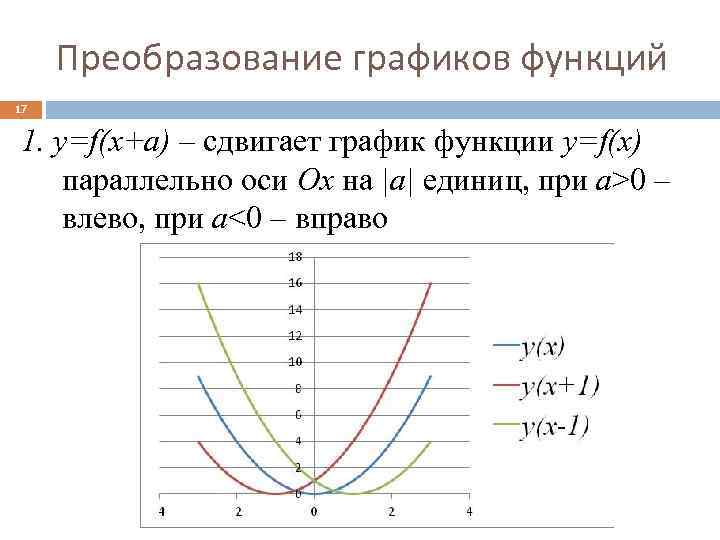Преобразование графиков функций 17 1. y=f(x+a) – сдвигает график функции y=f(x) параллельно оси Ox на |a| единиц, при a>0 – влево, при a<0 – вправо

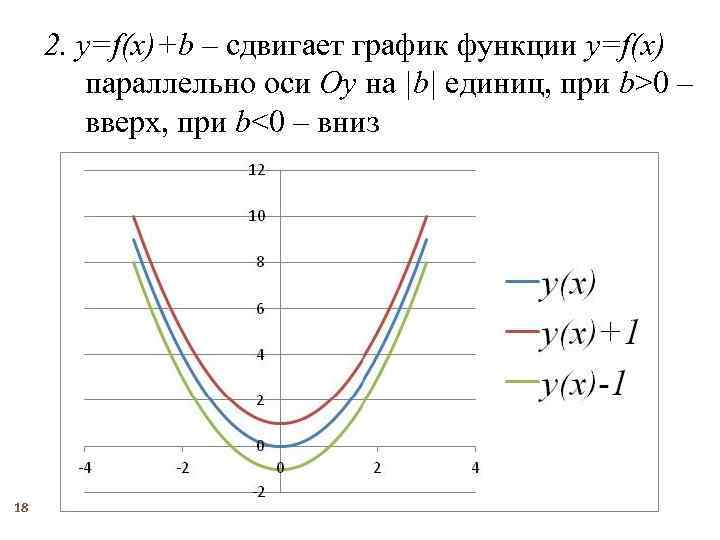2. y=f(x)+b – сдвигает график функции y=f(x) параллельно оси Oy на |b| единиц, при b>0 – вверх, при b<0 – вниз 18

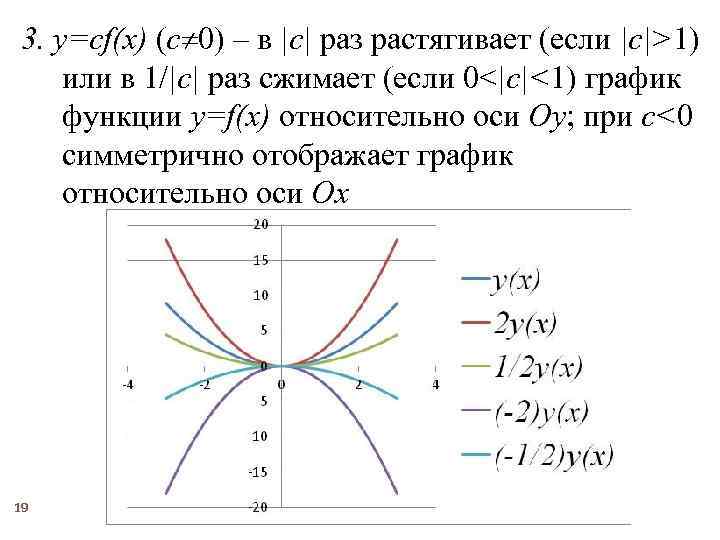3. y=cf(x) (c 0) – в |c| раз растягивает (если |c|>1) или в 1/|c| раз сжимает (если 0<|c|<1) график функции y=f(x) относительно оси Oy; при c<0 симметрично отображает график относительно оси Ox 19

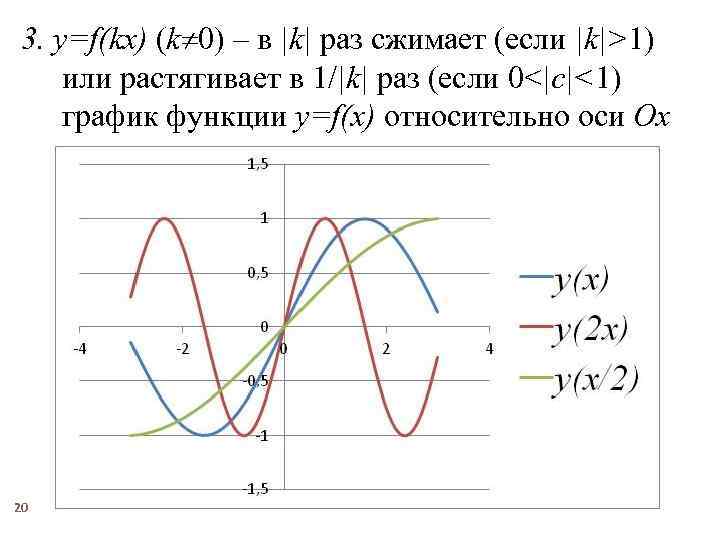3. y=f(kx) (k 0) – в |k| раз сжимает (если |k|>1) или растягивает в 1/|k| раз (если 0<|c|<1) график функции y=f(x) относительно оси Ox 20

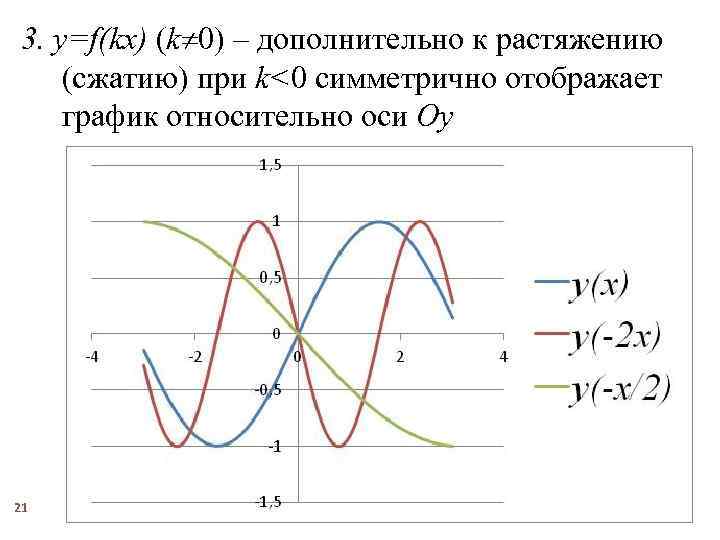3. y=f(kx) (k 0) – дополнительно к растяжению (сжатию) при k<0 симметрично отображает график относительно оси Oy 21

Пределы и непрерывность 22 Если по некоторому закону каждому натуральному числу n поставлено в соответствие определенное число an, то говорят, что задана числовая последовательность {an}. Число A называется пределом числовой последовательности {an}, если для любого >0 найдется номер такой N=N( ), что для всех n >N |an – A|<. Обозначение:

Число A называется пределом функции y=f(x) при x→∞, если для любого >0 найдется такое число S=S( )>0, что для всех x таких, что |x|>A выполняется неравенство |f(x) – A| < . Обозначение: Число A называется пределом функции y=f(x) при x→x 0, если для любого >0 найдется число δ=δ( )>0, что для всех x таких, что |x–x 0|<δ выполняется неравенство |f(x) – A| < . Обозначение: 23

Функция α(x) называется бесконечно малой величиной при x→x 0 (или x→∞), если или Функция f(x) называется бесконечно большой величиной при x→x 0, если для любого M >0 найдется число δ=δ(M)>0, что для всех x x 0 таких, что |x–x 0|<δ выполняется неравенство |f(x)| > M. Следовательно, 24

Свойства бесконечно малых 25 Если функции α(x) и (x) – бесконечно малые величины при x→x 0 (или x→∞), то будут бесконечно малыми величины: α(x) + (x), α(x) – (x), c ∙ α(x), где c=const, f(x) ∙ α(x), где f(x) – ограниченная функция, α(x) ∙ (x),

Свойства бесконечно больших 26 Если функция f(x) – бесконечно большая величина при x→x 0 (или x→∞), то будут бесконечно большими величины: f(x) + φ(x), f(x) – φ(x), где φ(x) – ограниченная функция,

27 Связь бесконечно больших и бесконечно малых Если функция f(x) – бесконечно большая величина при x→x 0 (или x→∞), то функция является бесконечно малой величиной, и наоборот, если α(x) – бесконечно малая величина при x→x 0 (или x→∞), то является бесконечно большой.

Непрерывность функций 28 Определение 1. Функция f(x) называется непрерывной в точке x 0 , если: 1) определена в точке x 0, 2) имеет конечный предел при x→x 0, 3) этот предел равен значению функции в этой точке:

Непрерывность функций 29 Определение 2. Функция f(x) называется непрерывной в точке x 0 , если: 1) определена в точке x 0, 2) бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции:

Свойства непрерывных функций 30 Если функции f(x) и φ(x) непрерывны в точке, то их сумма, произведение и частное (если знаменатель отличен от нуля) являются непрерывными в этой точке. Если функция f(u) непрерывна в точке u 0=φ(x 0), а функция u=φ(x) непрерывна в точке x 0, то сложная функция y=f(φ(x)) непрерывна в точке x 0:

Непрерывность функций 31 Определение 3. Функция f(x) называется непрерывной на некотором промежутке, если она непрерывна в любой точке этого промежутка. Если условия непрерывности не выполнены, то функция терпит разрыв в точке x 0

Точки разрыва функции 32 Если оба односторонних предела или конечны, но не равны между собой, то x 0 – точка неустранимого разрыва первого рода. Если оба односторонних предела конечны, равны между собой, но не равны f(x 0), то x 0 – точка устранимого разрыва первого рода.

Точки разрыва функции 33 Если хотя бы один из односторонних пределов функции f(x) в точке x 0 бесконечен, то x 0 – точка разрыва второго рода.

34