 Введение. Моделирование атомномолекулярных структур 1
Введение. Моделирование атомномолекулярных структур 1
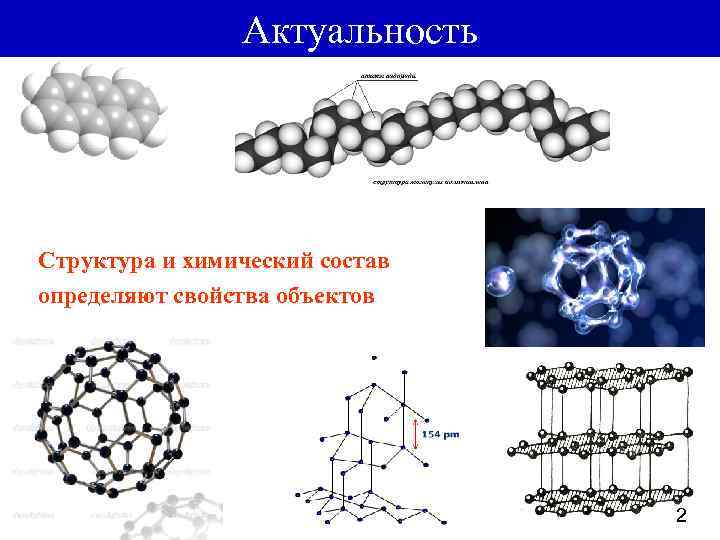 Актуальность Структура и химический состав определяют свойства объектов 2
Актуальность Структура и химический состав определяют свойства объектов 2
 Молекулярная динамика • Уравнения: Ковалентные взаимодействия Не ковалентные взаимодействия 3
Молекулярная динамика • Уравнения: Ковалентные взаимодействия Не ковалентные взаимодействия 3
 Силовое поле, эмпирические константы Большинство значений можно получить из высокоточных расчётов QM ab initio. Полученные значения "подгоняют" под уравнения силового поля. Константы из уравнения : 1) связи , Кb, b 0 2) углы K , 0 3) торсионные углы K , 4) Частичные заряды qi 5) Параметры Wd. V Aij, Cij ИК-спектроскопия, QM ИК-спектроскопия, ЯМР, QM угадывание, термодинамика, QM 4
Силовое поле, эмпирические константы Большинство значений можно получить из высокоточных расчётов QM ab initio. Полученные значения "подгоняют" под уравнения силового поля. Константы из уравнения : 1) связи , Кb, b 0 2) углы K , 0 3) торсионные углы K , 4) Частичные заряды qi 5) Параметры Wd. V Aij, Cij ИК-спектроскопия, QM ИК-спектроскопия, ЯМР, QM угадывание, термодинамика, QM 4
 Алгоритм Сумма сил действующих на атом Dt Расчет новых координат интегрирование 5
Алгоритм Сумма сил действующих на атом Dt Расчет новых координат интегрирование 5
 Возможности МД равновесные свойства: • Константы связи • Средняя потенциальная энергия системы • Равновесная геометрия динамические и неравновесные свойства: • • Вязкость жидкости Процесс диффузии в мембраны Динамика фазовых изменений Кинетику реакции Размеры систем – до 106 атомов!!! 6
Возможности МД равновесные свойства: • Константы связи • Средняя потенциальная энергия системы • Равновесная геометрия динамические и неравновесные свойства: • • Вязкость жидкости Процесс диффузии в мембраны Динамика фазовых изменений Кинетику реакции Размеры систем – до 106 атомов!!! 6
 Ограничения МД • • • Используются законы Ньютона Не учитываются электроны Силовые поля – это приближение Удаленные взаимодействия не учитываются Граничные условия не натуралистичны 7
Ограничения МД • • • Используются законы Ньютона Не учитываются электроны Силовые поля – это приближение Удаленные взаимодействия не учитываются Граничные условия не натуралистичны 7
 Квантовая химия • Атомная система единиц: • Стационарное уравнение Шрёдингера: • Для многочастичной системы: H, T, U – операторы Гамильтона, кинетической и потенциальной энергии; Z – заряд ядра; r – расстояние между частицами; Δ – оператор Лапласа; индексы a и b – номера ядер; i и j – номера электронов 8
Квантовая химия • Атомная система единиц: • Стационарное уравнение Шрёдингера: • Для многочастичной системы: H, T, U – операторы Гамильтона, кинетической и потенциальной энергии; Z – заряд ядра; r – расстояние между частицами; Δ – оператор Лапласа; индексы a и b – номера ядер; i и j – номера электронов 8
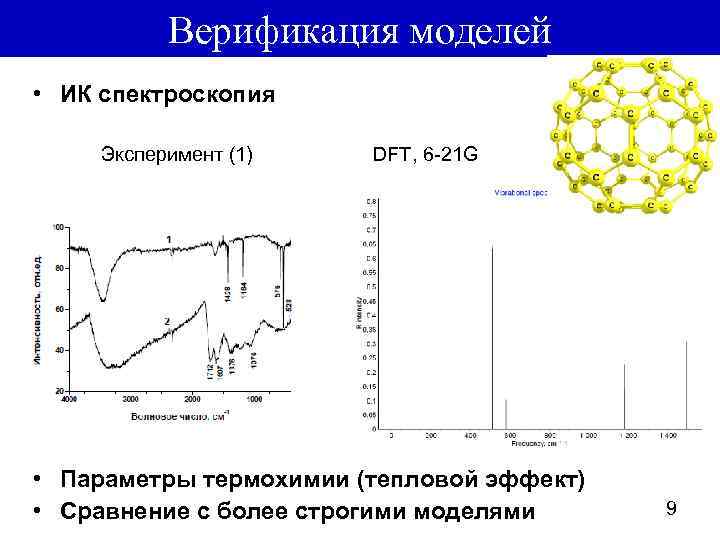 Верификация моделей • ИК спектроскопия Эксперимент (1) DFT, 6 -21 G • Параметры термохимии (тепловой эффект) • Сравнение с более строгими моделями 9
Верификация моделей • ИК спектроскопия Эксперимент (1) DFT, 6 -21 G • Параметры термохимии (тепловой эффект) • Сравнение с более строгими моделями 9
 Выводы § Теоретический инструментарий исследований в размерном диапазоне 10 -8 – 10 -10 существует § Ограничения: § Вычислительные ресурсы § Возможности программных пакетов § Начальные и граничные условия § Основные проблемы: § Постановка задачи § Обоснование выбранной модели § Анализ результатов 10
Выводы § Теоретический инструментарий исследований в размерном диапазоне 10 -8 – 10 -10 существует § Ограничения: § Вычислительные ресурсы § Возможности программных пакетов § Начальные и граничные условия § Основные проблемы: § Постановка задачи § Обоснование выбранной модели § Анализ результатов 10
 Стационарная теория возмущений. Невырожденный случай. 11
Стационарная теория возмущений. Невырожденный случай. 11
 Постановка задачи § Рассматривается возмущенное уравнение Шрёдингера: (1) § Пусть для невозмущенного оператора известно точное решение (2) § Требуется получить решение для возмущенного оператора 12
Постановка задачи § Рассматривается возмущенное уравнение Шрёдингера: (1) § Пусть для невозмущенного оператора известно точное решение (2) § Требуется получить решение для возмущенного оператора 12
 Решение. Учет малости возмущения § Учтем, что § Используя разложение в ряд Тейлора по степеням малого возмущения получим: (3) § Подставим (3) (1) и приравняем члены одинакового порядка малости. Получим (4) 13
Решение. Учет малости возмущения § Учтем, что § Используя разложение в ряд Тейлора по степеням малого возмущения получим: (3) § Подставим (3) (1) и приравняем члены одинакового порядка малости. Получим (4) 13
 Решение. Первая поправка к энергиям § Система собственных функций ортонормальна и полна § § Теорема о собственных функциях эрмитова оператора (Владимиров В. С. Уравнения математической физики. – М. , 1971. – С. 42 -43) Теорема Стеклова (Там же, С. 345 – 346) § Для первой поправки к энергии получим: (5’) (5) 14
Решение. Первая поправка к энергиям § Система собственных функций ортонормальна и полна § § Теорема о собственных функциях эрмитова оператора (Владимиров В. С. Уравнения математической физики. – М. , 1971. – С. 42 -43) Теорема Стеклова (Там же, С. 345 – 346) § Для первой поправки к энергии получим: (5’) (5) 14
 Решение. Первая поправка к ψ § Необходимо найти коэффициенты разложения (6) 15
Решение. Первая поправка к ψ § Необходимо найти коэффициенты разложения (6) 15
 Решение. Первая поправка к ψ § Коэффициент ann (7) 16
Решение. Первая поправка к ψ § Коэффициент ann (7) 16
 Результат § Первая поправка к энергии § Первая поправка к волновой функции § Ряд сходится при 17
Результат § Первая поправка к энергии § Первая поправка к волновой функции § Ряд сходится при 17
 Д. З. : Флюгге. Задачи по квантовой механике. Т. 2, № 181. Рассмотреть стационарный случай 18
Д. З. : Флюгге. Задачи по квантовой механике. Т. 2, № 181. Рассмотреть стационарный случай 18