Введение • Логика – наука о законах

Введение • Логика – наука о законах и формах мышления, методах познания и условия определения истинности знаний и суждений. • Формализация (логико-математическое представление) – процесс представления информации в формализованном виде с помощью точного логико-математического языка. • Логическая алгебра (алгебра Буля или алгебра высказываний) – раздел математической логики, изучающей логические законы с помощью формул, построенных на высказывательных константах, переменных и символов логических связок. • Необходимые знания: понимание логических процессов, происходящих при вводе, хранении и выводе информации в ЭВМ.

Словарь терминов Понятие (глоссарий) мышления, – форма фиксирующее основные свойства объектов. Высказывание (суждение, утверждение) – форма мышления, утверждающая или отрицающая определенные свойства объектов и связи между ними. Умозаключение – форма мышления, являющаяся получением новых знаний (суждений) – заключения из одного или нескольких суждений - посылок.

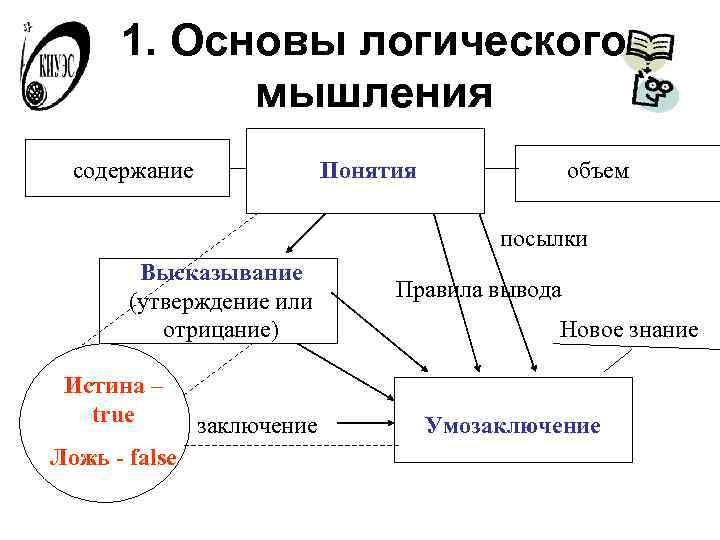1. Основы логического мышления содержание Понятия объем посылки Высказывание (утверждение или Правила вывода отрицание) Новое знание Истина – true заключение Умозаключение Ложь - false

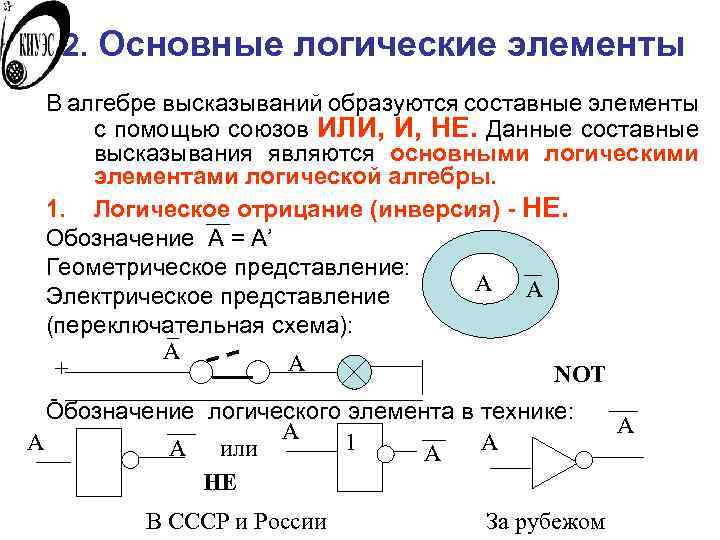2. Основные логические элементы В алгебре высказываний образуются составные элементы с помощью союзов ИЛИ, И, НЕ. Данные составные высказывания являются основными логическими элементами логической алгебры. 1. Логическое отрицание (инверсия) - НЕ. Обозначение A = A’ Геометрическое представление: A A Электрическое представление (переключательная схема): А А + NOT - Обозначение логического элемента в технике: А А А или 1 А А НЕ В СССР и России За рубежом

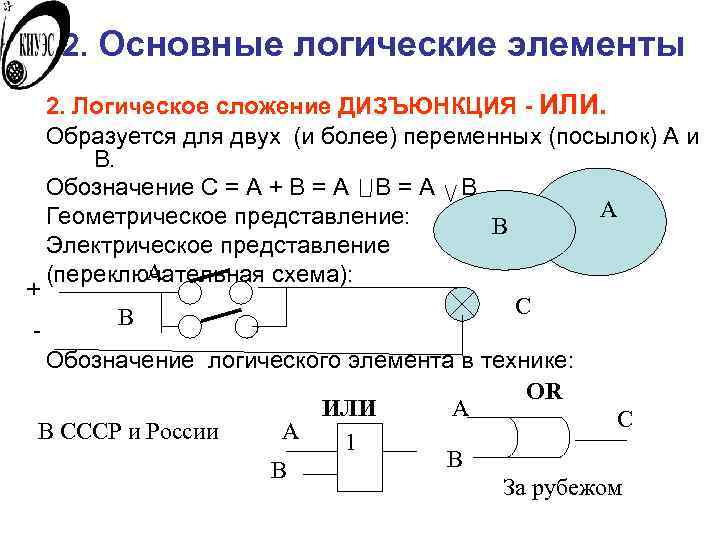2. Основные логические элементы 2. Логическое сложение ДИЗЪЮНКЦИЯ - ИЛИ. Образуется для двух (и более) переменных (посылок) A и B. Обозначение C = A + B = A B Геометрическое представление: A B Электрическое представление А (переключательная схема): + B C - Обозначение логического элемента в технике: OR ИЛИ А C В СССР и России А 1 B В За рубежом

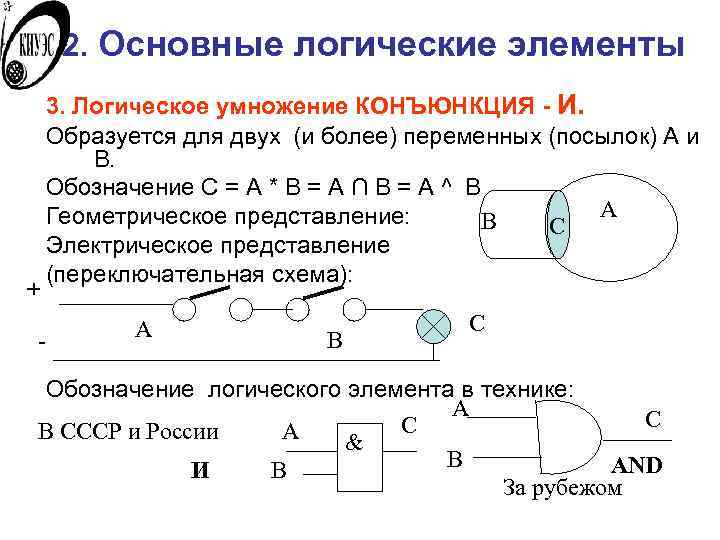2. Основные логические элементы 3. Логическое умножение КОНЪЮНКЦИЯ - И. Образуется для двух (и более) переменных (посылок) A и B. Обозначение C = A * B = A ∩ B = A ^ B Геометрическое представление: B A C Электрическое представление (переключательная схема): + А C - В Обозначение логического элемента в технике: А C В СССР и России А C & И B В AND За рубежом

3. Логические выражения, функции и таблицы истинности. Логическое выражение – это формула, в которую входят логические переменные, обозначающие высказывания, и знаки логических операций, обозначающие логические функции. Для записи составного высказывания в виде формального логического выражения нужно выделить простые высказывания и логические связи между ними. Таблица истинности – таблица, которая показывает, какие значения принимает логическая функция при всех возможных наборах ее аргументов (входных переменных). Количество строк в таблице истинности равно количеству возможных n значений входных логических переменных, т. е. 2 n. Количество столбцов равно сумме количества логических переменных и логических операций.

4. Законы логической алгебры Логические элементы И, ИЛИ, НЕ являются избыточными для формального представления, поэтому функции имеют нормальную дизъюнктивную форму (набор ИЛИ, НЕ) и нормальную конъюнктивную форму (набор И, НЕ). Поэтому законы логической алгебры представляют для двух форм. Основные законы логической алгебры Начало таблицы конъюнкция дизъюнкция A*0=0 A+0=A A*1=A A+1=1 A*A =A A+A=A

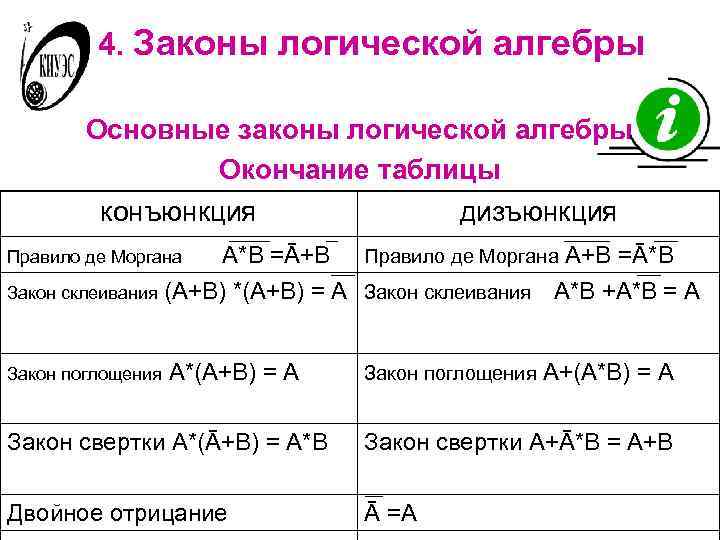4. Законы логической алгебры Основные законы логической алгебры Окончание таблицы конъюнкция дизъюнкция Правило де Моргана A*B =Ā+B Правило де Моргана A+B =Ā*B Закон склеивания (A+B) *(A+B) = A Закон склеивания A*B +A*B = A Закон поглощения A*(A+B) = A Закон поглощения A+(A*B) = A Закон свертки A*(Ā+B) = A*B Закон свертки A+Ā*B = A+B Двойное отрицание Ā =A