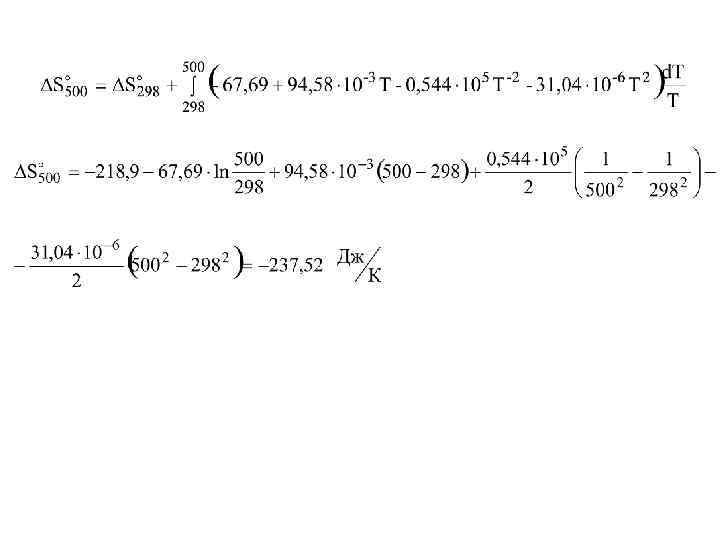Второй закон термодинамики 1747 г М В

Второй закон термодинамики • 1747 г. М. В. Ломоносов «…холодное тело В, погруженное в теплое тело А, не может воспринять большую степень теплоты, чем какую имеет А» • 1824 г. Сади Карно – условия превращения теплоты в полезную работу

• 1850 г. Клаузиус • 1854 г. Томсон (Лорд Кельвин) • Формулировка Клаузиуса: «Невозможен самопроизвольный переход тепла от менее нагретого тела к более нагретому» • «Невозможно создать вечный двигатель второго рода, т. е. машину, которая периодически превращает тепло среды при постоянной температуре в работу»

Необратимые и обратимые процессы • Необратимые процессы – процессы, в которых энтропия увеличивается. - переход тепла от теплого тела к холодному; - расширение газа в пустоту; - взаимная диффузия газов или жидкостей

• Обратимые процессы – процессы, при которых энтропия остается постоянной. • Обратимым называется процесс посредством которого можно вернуть систему в исходное состояние, не произведя никаких изменений ни в самой системе, ни в окружающей среде.

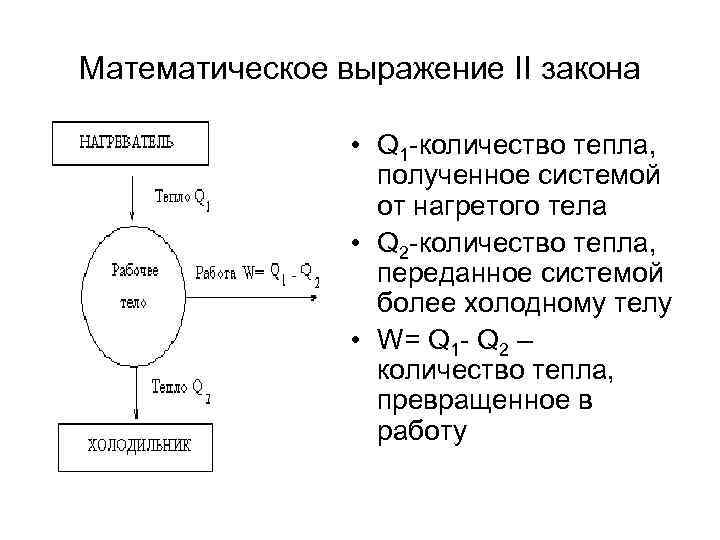Математическое выражение II закона • Q 1 -количество тепла, полученное системой от нагретого тела • Q 2 -количество тепла, переданное системой более холодному телу • W= Q 1 - Q 2 – количество тепла, превращенное в работу

• Коэффициент полезного действия

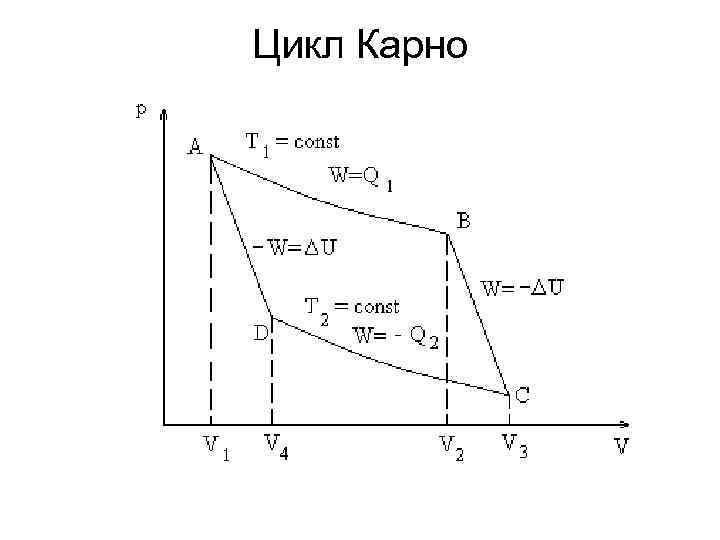Цикл Карно

• А В Производство работы, совершаемой за счет подводимого к системе тепла. (1) • В С Убыль внутренней энергии (2)

• С D Работа, затраченная на сжатие, переходит в отдаваемое окружающей среде тепло: (3) • D A Затраченная работа расходуется на увеличение внутренней энергии (4)

(5) Для адиабаты ВС Для адиабаты DA (6) (7)

Разделив уравнение (6) на (7), получим: или Уравнение (5) представим так: (8) Разделим уравнение (8) на уравнение (1): (9)

Уравнение (9) можно представить в ином виде: Коэффициент полезного действия цикла Карно ( ) всегда больше коэффициента полезного действия любого кругового цикла ( ’), состоящего из необратимых процессов.

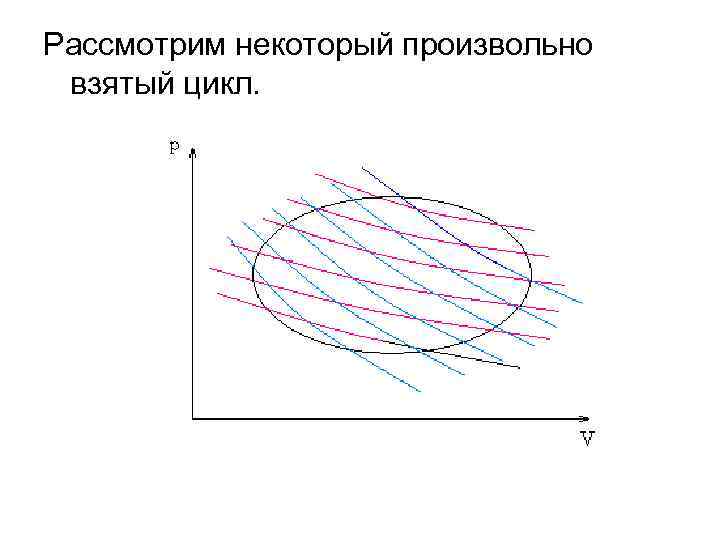Рассмотрим некоторый произвольно взятый цикл.

Для каждого из бесконечно малых циклов справедливы равенства: и т. д. Суммируем эти равенства:

В пределе алгебраическая сумма переходит в интеграл по замкнутому контуру

• Энтропия – S • - для обратимых процессов • Для необратимых процессов

• Математическая формулировка второго начала термодинамики: или Знак > - для необратимого процесса Знак = - для обратимого процесса

• Энтропия является функцией состояния. • Энтропия является аддитивным свойством. Это означает, что энтропия системы равна сумме энтропий составных частей. • Энтропия является мерой разупорядоченности вещества. • Размерность энтропии – единицы энергии деленные на градус (Дж/моль. К) • Энтропия характеризует количество энергии отнесенное к 1 данной температуры.

Вычисление изменения энтропии при различных процессах. • Изобарический процесс (p=const)

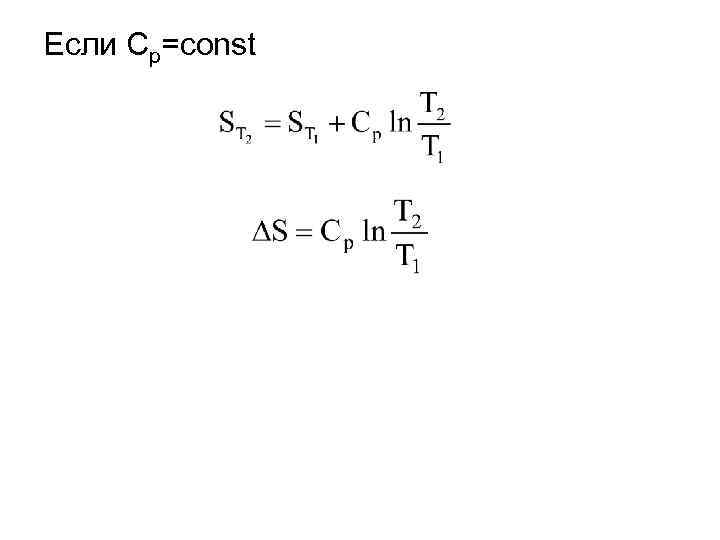Если Ср=const

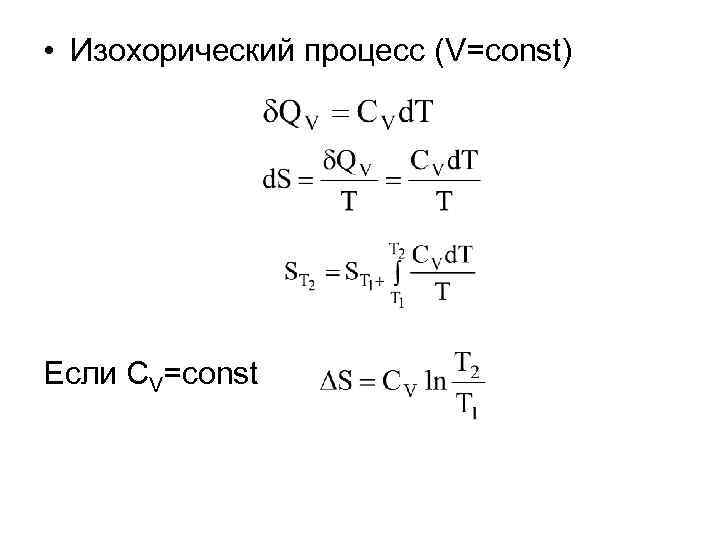• Изохорический процесс (V=const) Если CV=const

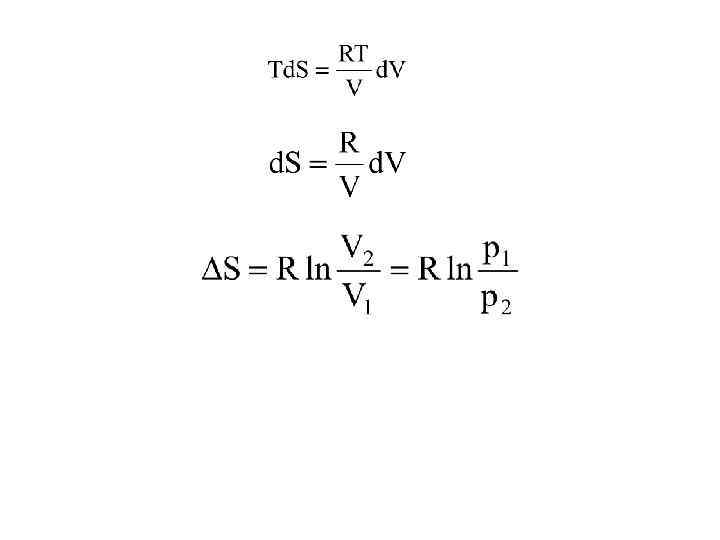
• Изотермический процесс (T=const) d. U=0

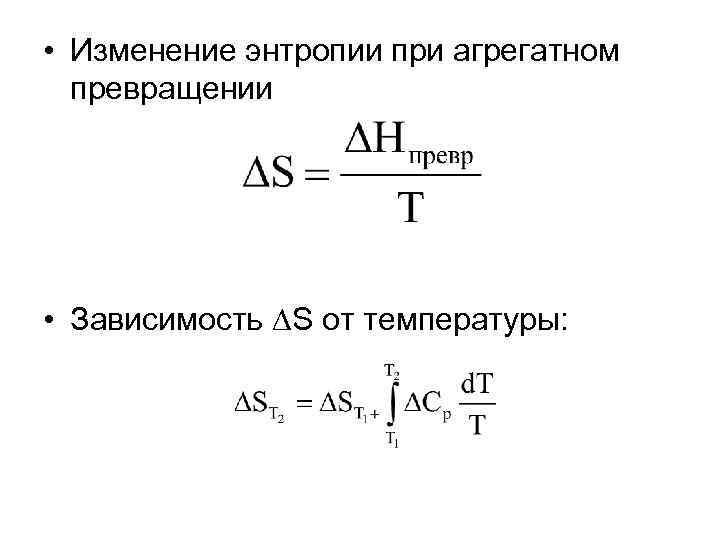• Изменение энтропии при агрегатном превращении • Зависимость S от температуры:

• Рассчитайте изменение энтропии при реакции 2 H 2(газ)+СО(газ)=СН 3 ОН(газ) при температуре 500 К с помощью таблиц стандартных термодинамических величин.

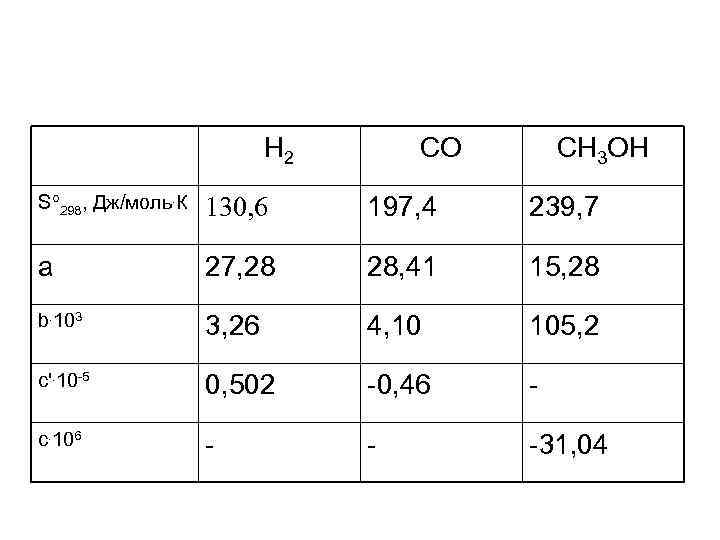Н 2 СО СН 3 ОН S 298, Дж/моль. К 130, 6 197, 4 239, 7 а 27, 28 28, 41 15, 28 b. 103 3, 26 4, 10 105, 2 c'. 10 -5 0, 502 -0, 46 - c. 106 - - -31, 04

а = 15, 28 -28, 41 -2. 27, 28 = - 67, 69 b = 105, 2 -4, 10 -2. 3, 26 = 94, 58 с’=0, 46 -2. 0, 502 = -0, 544 с = -31, 04 Сp= -67, 69+94, 58. 10 -3. Т-0, 544. 105 Т-2 -31, 04. 10 -6 Т 2