Второе начало термодинамики Первое начало термодинамики это

Второе начало термодинамики Первое начало термодинамики – это обобщение закона сохранения энергии на тепловые процессы. Оказывается, однако, что не все процессы разрешённые первым началом термодинамики возможны. Второе начало термодинамики формулирует эти ограничения. Второй закон термодинамики непосредственно связан с необратимостью реальных тепловых процессов. Энергия теплового движения молекул качественно отличается от всех других видов энергии – механической, электрической, химической и т. д. Энергия любого вида, кроме энергии теплового движения молекул, может полностью превратиться в любой другой вид энергии, в том числе и в энергию теплового движения. Последняя может испытать превращение в любой другой вид энергии лишь частично. Поэтому любой физический процесс, в котором происходит превращение какого-либо вида энергии в энергию теплового движения молекул, является необратимым процессом, т. е. он не может быть осуществлен полностью в обратном направлении.

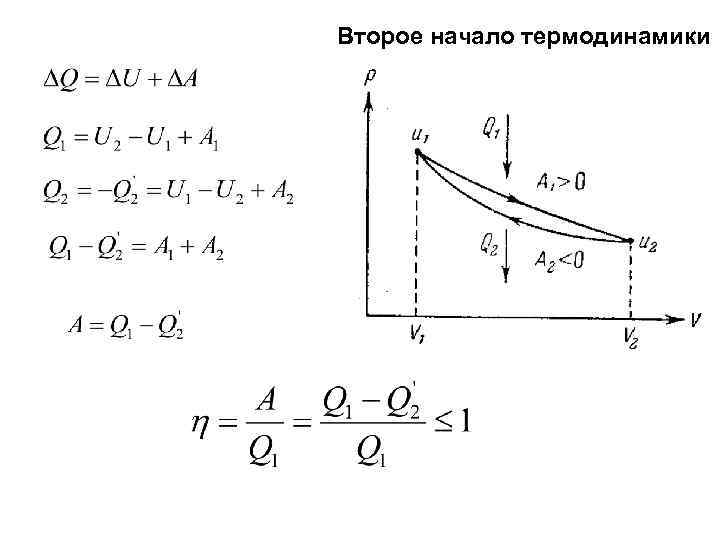Второе начало термодинамики

Второе начало термодинамики Другая форма формулировки Кельвина Невозможно создать тепловой двигатель с КПД η=1, или невозможен вечный двигатель 2 -го рода.

Второе начало термодинамики Вечный двигатель второго рода — воображаемая машина, которая, превращала бы в работу всё тепло, извлекаемое из окружающих тел. Если бы тепловой двигатель с КПД =1 был возможен, т. е. если бы всё тепло могло превращаться в работу (Q 2=0), мы не нуждались бы в более холодных телах и могли бы совершать работу за счёт отбора тепла из окружающих нас тел, например, от океана. В силу практической безграничности такого источника тепловой энергии это был бы вечный двигатель (второго рода).

Второе начало термодинамики Энтропия Понятие энтропии было введено Клаузиусом (1865) и является характеристикой необратимости процессов. Понятие энтропии играет важную роль не только в физике, но и в теории информации. Энтропия вводится через её изменение (как часто делается в физике). В дифференциальной форме , Рудольф Клаузиус 1822 -1888 Можно доказать, . что энтропия (или «приведённое тепло» ) является функцией состояния (несмотря на то что количество теплоты функцией состояния не является. Изменение энтропии при переходе системы из состояния 1 в состояние 2 в равновесном процессе S 2 – S 1 не зависит от вида процесса. S 2 – S 1 определяется лишь начальным и конечным состояниями.

Второе начало термодинамики Энтропия При таком введении энтропии можно вычислять только разность энтропий для разных состояний системы, но не саму величину , энтропии. Энтропия определяется с точностью до постоянной. Однако, используя третье начало термодинамики (теорема Нернста), согласно которому энтропия любой системы при температуре абсолютного нуля равна 0, можно найти и величину самой энтропии.

Второе начало термодинамики Энтропия Важнейшее свойство энтропии: Энтропия замкнутой (т. е. теплоизолированной)_ макросистемы не уменьшается – она либо возрастает, либо остаётся постоянной. Ещё одна формулировка 2 -го В замкнутых системах: начала В случае обратимых процессов энтропия замкнутой макросистемы не меняется В случае необратимых процессов энтропия замкнутой макросистемы возрастает Таким образом, величина возрастания энтропии в замкнутой системе может служить мерой необратимости процессов, протекающих в системе. Анализ изменения энтропии даёт указание, в каком направлении могут происходить самопроизвольные необратимые процессы в замкнутой системе: в сторону возрастания энтропии.

Второе начало термодинамики Энтропия Пример необратимого процесса в замкнутой системе. Замкнутая макросистема: два теплоизолированных сосуда разделённых перегородкой с вентилем. Равновесное состояние 1. В сосуде 1 находится 1 моль идеального газа. В сосуде 2 – вакуум. После того как вентиль открыли газ адиабатически расширился и заполнил объём 2. После того как давление и температура уравнялась образовалось равновесное состояние 2. Переход очевидно необратимый. Должно быть S 2 -S 1>0. Проверим. Энтропия функция состояния. S 2 -S 1 не зависит от пути перехода. Поэтому выберем такой путь на котором легче найти S 2 -S 1. Поскольку переход был адиабатический и работа не совершалась внутренняя энергия газа не изменилась, следовательно температура в равновесных состояниях 1 и 2 одна и та же.

Второе начало термодинамики Энтропия Следовательно для нахождения изменения энтропии можно использовать изотермический процесс (энтропия – функция состояния). В случае изотермического процесса Обратный процесс невозможен

Расширение газа в замкнутой системе приводит к росту энтропии. Согласно второму началу (в замкнутых системах ) расширение газа в замкнутой системе – необратимый процесс. Самопроизвольно он может протекать лишь в одну сторону. Обратный процесс (самопроизвольное сжатие) запрещён вторым началом (поскольку энтропия при этом снижается). Таким образом, анализ изменения энтропии указывает, какие неравновесные процессы в замкнутой системе возможны (протекают самопроизвольно), а какие нет.