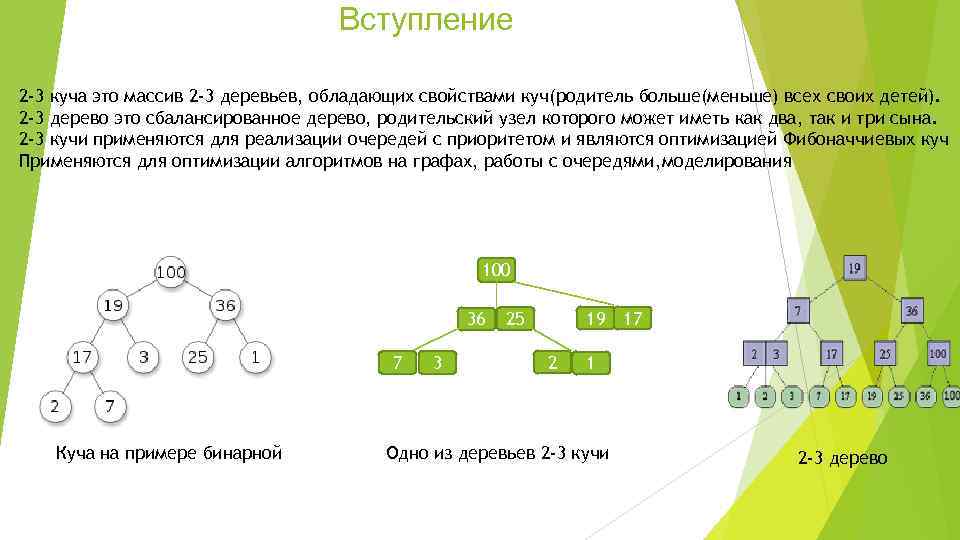
 Вступление 2 -3 куча это массив 2 -3 деревьев, обладающих свойствами куч(родитель больше(меньше) всех своих детей). 2 -3 дерево это сбалансированное дерево, родительский узел которого может иметь как два, так и три сына. 2 -3 кучи применяются для реализации очередей с приоритетом и являются оптимизацией Фибоначчиевых куч Применяются для оптимизации алгоритмов на графах, работы с очередями, моделирования 100 36 7 Куча на примере бинарной 3 19 25 2 17 1 Одно из деревьев 2 -3 кучи 2 -3 дерево
Вступление 2 -3 куча это массив 2 -3 деревьев, обладающих свойствами куч(родитель больше(меньше) всех своих детей). 2 -3 дерево это сбалансированное дерево, родительский узел которого может иметь как два, так и три сына. 2 -3 кучи применяются для реализации очередей с приоритетом и являются оптимизацией Фибоначчиевых куч Применяются для оптимизации алгоритмов на графах, работы с очередями, моделирования 100 36 7 Куча на примере бинарной 3 19 25 2 17 1 Одно из деревьев 2 -3 кучи 2 -3 дерево
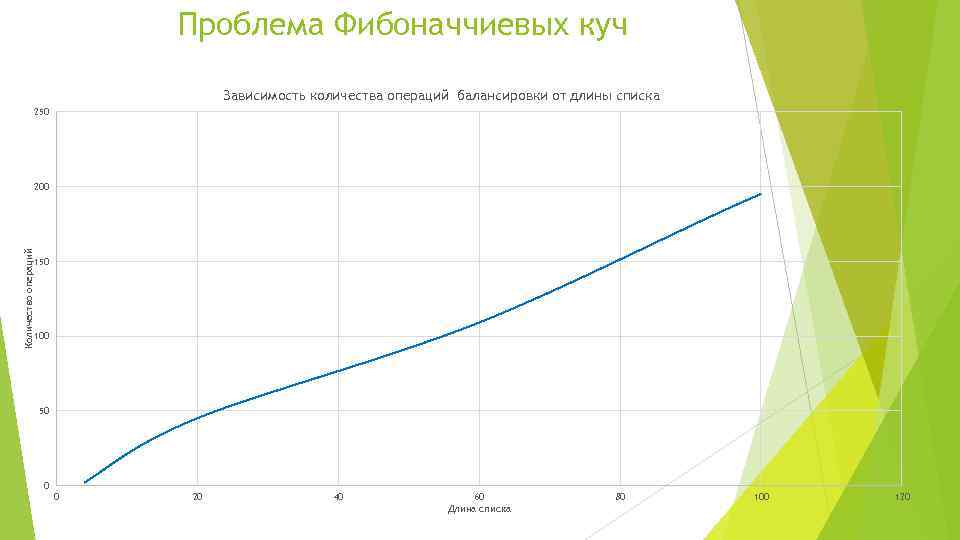 Проблема Фибоначчиевых куч Зависимость количества операций балансировки от длины списка 250 Количество операций 200 150 100 50 0 0 20 40 60 Длина списка 80 100 120
Проблема Фибоначчиевых куч Зависимость количества операций балансировки от длины списка 250 Количество операций 200 150 100 50 0 0 20 40 60 Длина списка 80 100 120
 Структура 2 -3 кучи Степень дерева – высота корневого узла Насыщенность дерева – возможность добавлять в дерево вершины без увеличения его степени Деревья бывают насыщенные(t) и ненасыщенные(f) В куче хранится массив деревьев по следующему принципу: В i-ой ячейке дерева располагается только дерево степени i Куча из 16 элементов (общий вид)
Структура 2 -3 кучи Степень дерева – высота корневого узла Насыщенность дерева – возможность добавлять в дерево вершины без увеличения его степени Деревья бывают насыщенные(t) и ненасыщенные(f) В куче хранится массив деревьев по следующему принципу: В i-ой ячейке дерева располагается только дерево степени i Куча из 16 элементов (общий вид)
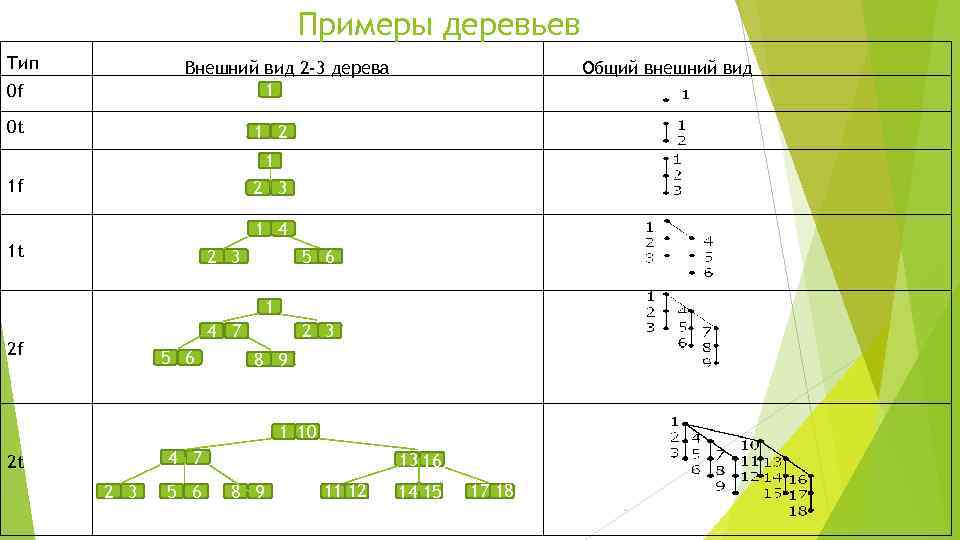 Примеры деревьев Тип Общий внешний вид Внешний вид 2 -3 дерева 1 0 f 0 t 1 2 1 1 f 2 3 1 4 1 t 2 3 5 6 1 4 7 2 f 5 6 2 3 8 9 1 10 4 7 2 t 2 3 5 6 13 16 8 9 11 12 14 15 17 18
Примеры деревьев Тип Общий внешний вид Внешний вид 2 -3 дерева 1 0 f 0 t 1 2 1 1 f 2 3 1 4 1 t 2 3 5 6 1 4 7 2 f 5 6 2 3 8 9 1 10 4 7 2 t 2 3 5 6 13 16 8 9 11 12 14 15 17 18
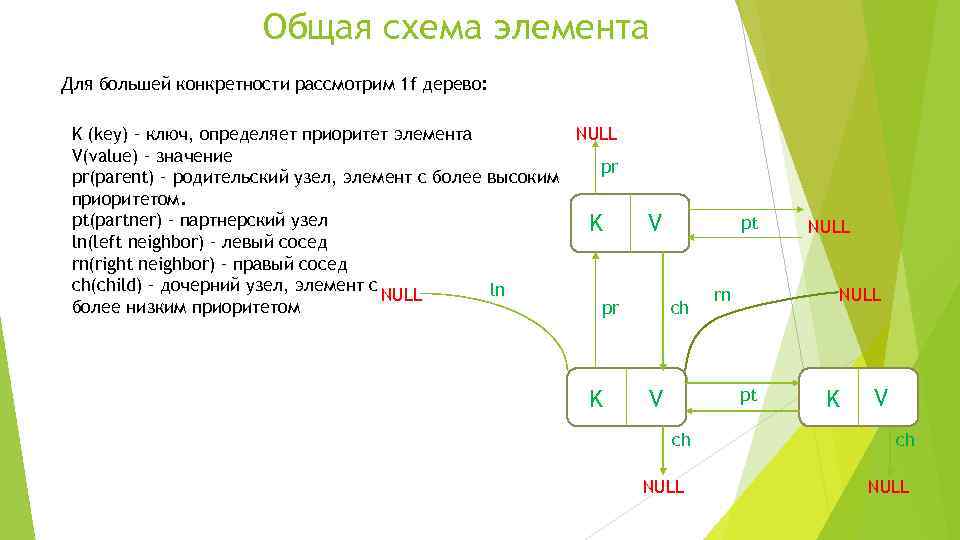 Общая схема элемента Для большей конкретности рассмотрим 1 f дерево: K (key) – ключ, определяет приоритет элемента NULL V(value) – значение pr pr(parent) – родительский узел, элемент с более высоким приоритетом. pt(partner) – партнерский узел K ln(left neighbor) – левый сосед rn(right neighbor) – правый сосед сh(child) – дочерний узел, элемент с ln NULL более низким приоритетом pr K V pt ch rn NULL pt V ch NULL K V ch NULL
Общая схема элемента Для большей конкретности рассмотрим 1 f дерево: K (key) – ключ, определяет приоритет элемента NULL V(value) – значение pr pr(parent) – родительский узел, элемент с более высоким приоритетом. pt(partner) – партнерский узел K ln(left neighbor) – левый сосед rn(right neighbor) – правый сосед сh(child) – дочерний узел, элемент с ln NULL более низким приоритетом pr K V pt ch rn NULL pt V ch NULL K V ch NULL
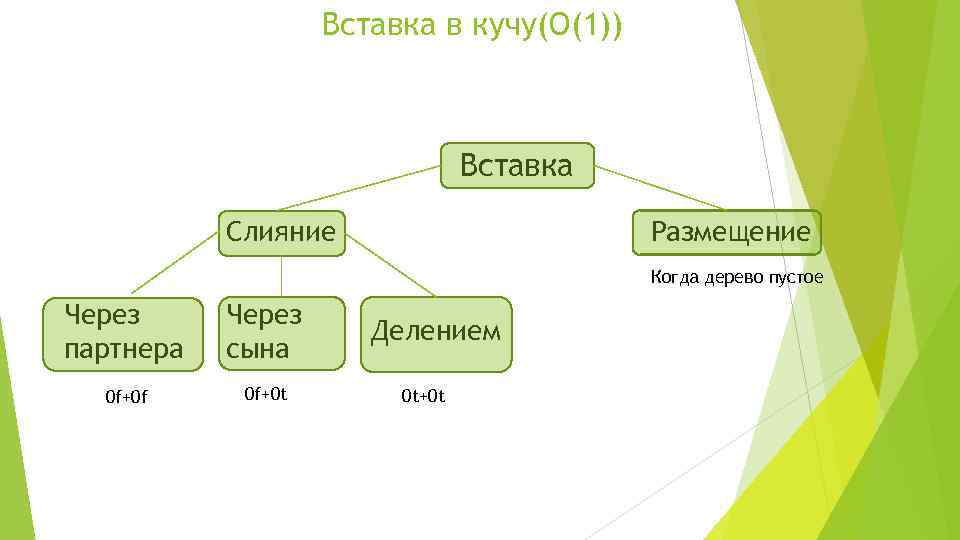 Вставка в кучу(O(1)) Вставка Слияние Размещение Когда дерево пустое Через партнера Через сына 0 f+0 f 0 f+0 t Делением 0 t+0 t
Вставка в кучу(O(1)) Вставка Слияние Размещение Когда дерево пустое Через партнера Через сына 0 f+0 f 0 f+0 t Делением 0 t+0 t
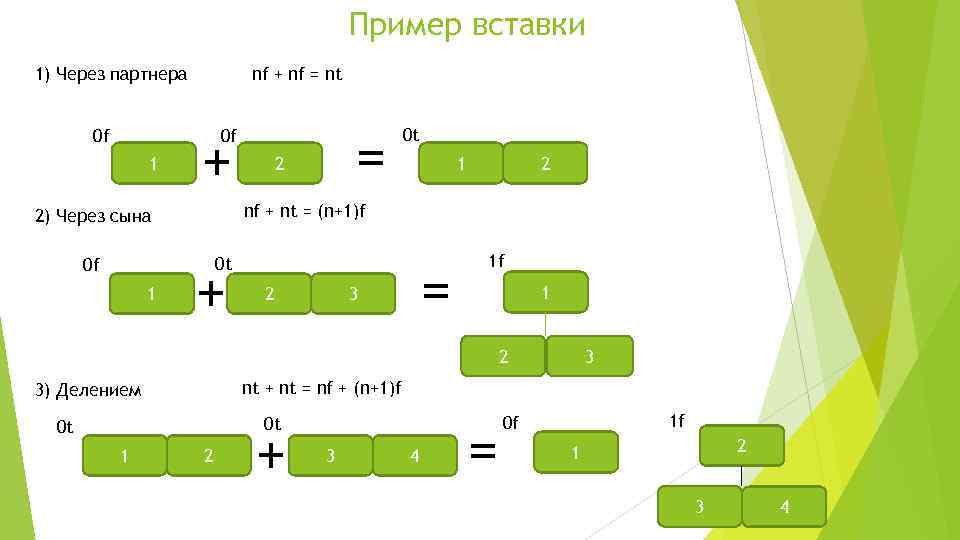 Пример вставки nf + nf = nt 1) Через партнера 0 f + = 0 f 1 2 0 t nf + nt = (n+1)f 2) Через сына 0 t 0 f 1 2 1 + 2 = 3 1 f 1 3 2 nt + nt = nf + (n+1)f 3) Делением 0 t 0 t 1 2 + 3 4 = 1 f 0 f 2 1 3 4
Пример вставки nf + nf = nt 1) Через партнера 0 f + = 0 f 1 2 0 t nf + nt = (n+1)f 2) Через сына 0 t 0 f 1 2 1 + 2 = 3 1 f 1 3 2 nt + nt = nf + (n+1)f 3) Делением 0 t 0 t 1 2 + 3 4 = 1 f 0 f 2 1 3 4
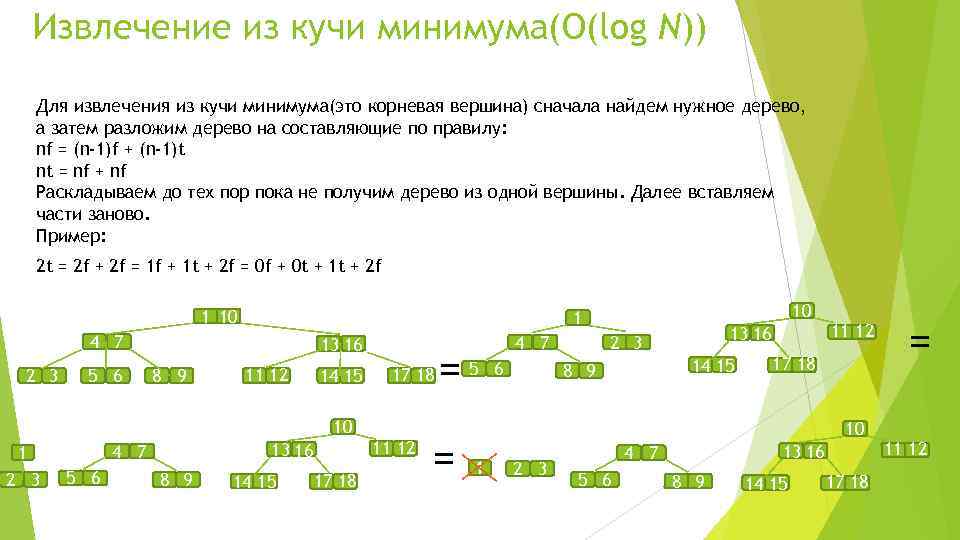 Извлечение из кучи минимума(O(log N)) Для извлечения из кучи минимума(это корневая вершина) сначала найдем нужное дерево, а затем разложим дерево на составляющие по правилу: nf = (n-1)f + (n-1)t nt = nf + nf Раскладываем до тех пор пока не получим дерево из одной вершины. Далее вставляем части заново. Пример: 2 t = 2 f + 2 f = 1 f + 1 t + 2 f = 0 f + 0 t + 1 t + 2 f 1 10 4 7 2 3 5 6 13 16 8 9 11 12 14 15 10 2 3 13 16 4 7 1 5 6 8 9 10 1 14 15 17 18 11 12 =5 = 4 7 6 13 16 2 3 14 15 8 9 11 12 17 18 10 1 2 3 13 16 4 7 5 6 8 9 14 15 17 18 = 11 12
Извлечение из кучи минимума(O(log N)) Для извлечения из кучи минимума(это корневая вершина) сначала найдем нужное дерево, а затем разложим дерево на составляющие по правилу: nf = (n-1)f + (n-1)t nt = nf + nf Раскладываем до тех пор пока не получим дерево из одной вершины. Далее вставляем части заново. Пример: 2 t = 2 f + 2 f = 1 f + 1 t + 2 f = 0 f + 0 t + 1 t + 2 f 1 10 4 7 2 3 5 6 13 16 8 9 11 12 14 15 10 2 3 13 16 4 7 1 5 6 8 9 10 1 14 15 17 18 11 12 =5 = 4 7 6 13 16 2 3 14 15 8 9 11 12 17 18 10 1 2 3 13 16 4 7 5 6 8 9 14 15 17 18 = 11 12
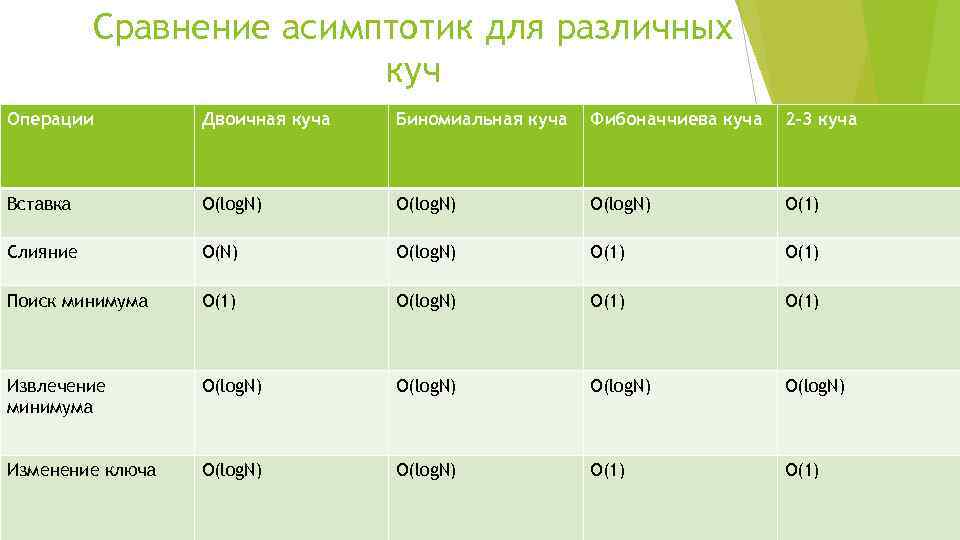 Сравнение асимптотик для различных куч Операции Двоичная куча Биномиальная куча Фибоначчиева куча 2 -3 куча Вставка O(log. N) O(1) Слияние O(N) O(log. N) O(1) Поиск минимума O(1) O(log. N) O(1) Извлечение минимума O(log. N) Изменение ключа O(log. N) O(1)
Сравнение асимптотик для различных куч Операции Двоичная куча Биномиальная куча Фибоначчиева куча 2 -3 куча Вставка O(log. N) O(1) Слияние O(N) O(log. N) O(1) Поиск минимума O(1) O(log. N) O(1) Извлечение минимума O(log. N) Изменение ключа O(log. N) O(1)
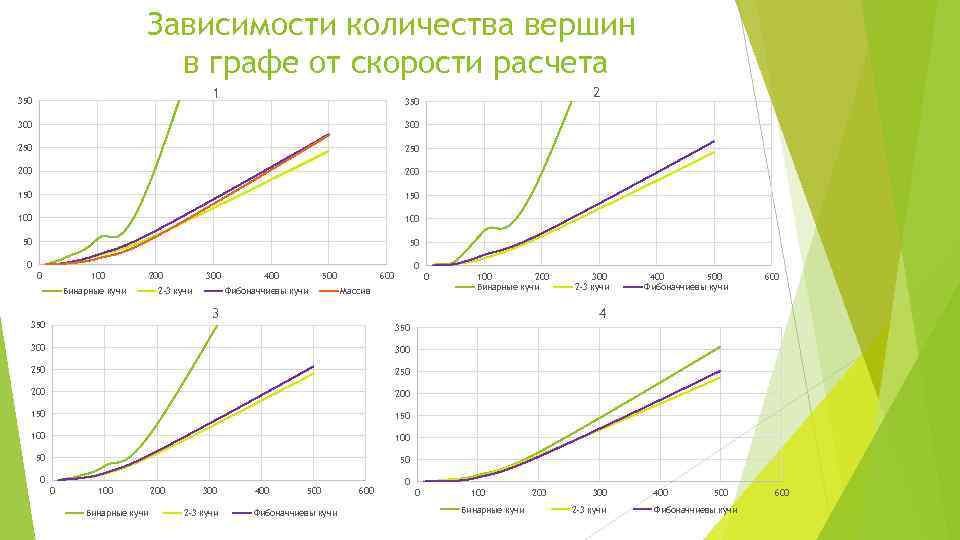 Зависимости количества вершин в графе от скорости расчета 1 350 2 350 300 250 200 150 100 50 50 0 0 100 Бинарные кучи 200 300 2 -3 кучи 400 500 Фибоначчиевы кучи 0 600 0 Массив 100 200 Бинарные кучи 3 350 300 2 -3 кучи 400 500 Фибоначчиевы кучи 600 4 350 300 250 200 150 100 50 50 0 0 100 Бинарные кучи 200 300 2 -3 кучи 400 500 Фибоначчиевы кучи 600
Зависимости количества вершин в графе от скорости расчета 1 350 2 350 300 250 200 150 100 50 50 0 0 100 Бинарные кучи 200 300 2 -3 кучи 400 500 Фибоначчиевы кучи 0 600 0 Массив 100 200 Бинарные кучи 3 350 300 2 -3 кучи 400 500 Фибоначчиевы кучи 600 4 350 300 250 200 150 100 50 50 0 0 100 Бинарные кучи 200 300 2 -3 кучи 400 500 Фибоначчиевы кучи 600
 Литература 1. C. A. Crane. Linear lists and priority queues as balanced binary trees. — Computer Science Dept, Stanford Univ. (1972). 2. Tadao Takaoka. Theory of 2 -3 Heaps. — Cocoon (1999). 3. Кормен Т. , Лейзерсон Ч. , Ривест Р. Алгоритмы: построение и анализ. — М. : МЦНМО, 2001. — С. 376 -409.
Литература 1. C. A. Crane. Linear lists and priority queues as balanced binary trees. — Computer Science Dept, Stanford Univ. (1972). 2. Tadao Takaoka. Theory of 2 -3 Heaps. — Cocoon (1999). 3. Кормен Т. , Лейзерсон Ч. , Ривест Р. Алгоритмы: построение и анализ. — М. : МЦНМО, 2001. — С. 376 -409.


