Временные ряды в эконометрических

Модели на основе рядов динамики p Модели изолированного динамического ряда.

Компоненты временного ряда p Тенденция (T) p Периодические колебания (P) p

p Ряд с периодическими и p Ряд с тенденцией, случайными

p. Аддитивная модель p. Мультипликативная модель

Автокорреляция уровней ряда и ее послед p Корреляционная зависимость между последовательными значениями уровней

Пример p. Имеются данные о расходах на конечное потребление и

Этапы построения модели тенденци (уравнения тренда) p Выбор математической функции,

Виды математических функций, описывающих тенденцию p Функции с монотонным

Парабола третьей степени p Этот вид тренда предполагает, что по

Логарифмическая парабола p Применяется, если стабильны - коэффициенты опережения темпов

Полулогарифмическая кривая (логарифмический тренд) p Применяется при замедленном росте

Степенной тренд p При b > 0 она характеризует

Степенной тренд p p - базисный коэффициент роста p

Кривые с насыщением p Гиперболы – кривые, характеризующие наличие

Модифицированная экспонента p Характеризуется постоянным отношением последовательных во времени приростов:

Пример (модифицированная экспонент Уровень Год

ВЫВОД ИТОГОВ Регрессионная статистика Множествен ный R 0, 990535 R-квадрат

ln. Y=lna+tlnb lna=3, 27231 lnb=-0, 22599

p Приведение к линейному виду модифицированной экспоненты (асимптота с задана исследователем):

Логистическая кривая p Подходит для описания такого процесса, при котором изучаемый

Логистическая кривая p c – верхняя асимптота

Пример (логистическая кривая с заданн асимптотой) Производство Год продукции, млн

ВЫВОД ИТОГОВ Регрессионна я статистика Множествен ный R

Кривая Гомперца–( образная кривая) S p Применяется

Использование трендовых моделей д прогнозирования

Моделирование периодических колеб p Ряды могут содержать только периодические колебания p

p Для выявления измерения периодических колебаний во временных рядах можно использовать метод

Ряд Фурье p Ряд Фурье -один из методов моделирования временного

Моделирование периодических колеб p Ряд Фурье можно описать в виде функции: p

Методы исключения тенденции при моделировани взаимосвязей по временным рядам p Метод

p прогнозное значение уровня ряда p конечный уровень динамического

Включение в модель регрессии по временным фактора времени

Анализ взаимосвязи по временным рядам ПРИМЕР

Пример Исключение тенденции методом первых разносте

Пример Исключение тенденции методом включения в модель регресс

Автокорреляция в остатках. Критери Дарбина-Уотсона

Обобщенный метод наименьших квадратов при построении модели регре временным рядам

По данным за 1995 -2003 гг. по Тамбовской области рассматривается зависимость потребления растительного

Расчет преобразованных значений p и т. д.

Учет сезонности при построении мод регрессии p z 1 = 1

p для I квартала p для II квартала p для

Пример. Объем продаж товара фирмой (у – тыс. ед. ) исследуется в зависим объема

Моделирование сезонных колебаний p Аддитивная модель p Мультипликативная модель

Расчет сезонной компоненты в аддитивной модели

Расчет средних значений сезонной компоненты в адди модели

Пример 1 (прогнозирование на основе аддитивной м

Пример (прогнозирование на основе аддитивной мо

Пример 2 Построение мультипликативной модели

Пример 2 (прогнозирование на основе мультипликативной модели)

МОДЕЛИ С ЛАГОВЫМИ ПЕРЕМЕННЫМИ p 1) модели с лаговыми

Модель с распределенными лагами p Данная модель означает, что изменение во

p Коэффициент - краткосрочный мультипликатор. Он характеризует среднее изменение результата y при изменении

Промежуточные мультипликаторы p при k=4: p

p Долгосрочный мультипликатор p При k=4 долгосрочный мультипликатор составит p

Относительные коэффициенты модели p Характеризует долю общего изменения y

Средняя величина лага p Показывает средний интервал времени, в

Медианный лаг p тот период времени, в течение которого с момента

p Рост инвестиций на 1 млн. руб. в текущем периоде приводит к росту

p Относительные коэффициенты модели: p = 0, 7 / 4 =

Скачать презентацию Временные ряды в эконометрических

Временные ряды.ppt

Количество слайдов: 81

> Временные ряды в эконометрических исследованиях 1. Специфика временного ряда как Временные ряды в эконометрических исследованиях 1. Специфика временного ряда как источника данных в эконометрическом моделировании. 2. Автокорреляция уровней ряда и ее последствия. 3. Моделирование тенденций временного ряда. 4. Использование трендовых моделей для прогнозирования. 5. Моделирование периодических колебаний. 6. Моделирование взаимосвязей по временным рядам. Методы исключения тенденции. 7. Автокорреляция в остатках. Критерий Дарбина- Уотсона. 8. Обобщенный метод наименьших квадратов при построении модели регрессии по временным рядам. 9. Сезонные колебания их учет при построении эконометрических моделей. 10. Модели с лаговыми переменными. Метод инструментальных переменных. Метод Алмон.

> Модели на основе рядов динамики p Модели изолированного динамического ряда. Модели на основе рядов динамики p Модели изолированного динамического ряда. p Модели системы взаимосвязанных рядов динамики. p Модели автрегрессии. p Модели с распределенным лагом.

> Компоненты временного ряда p Тенденция (T) p Периодические колебания (P) p Компоненты временного ряда p Тенденция (T) p Периодические колебания (P) p Случайные колебания (E)

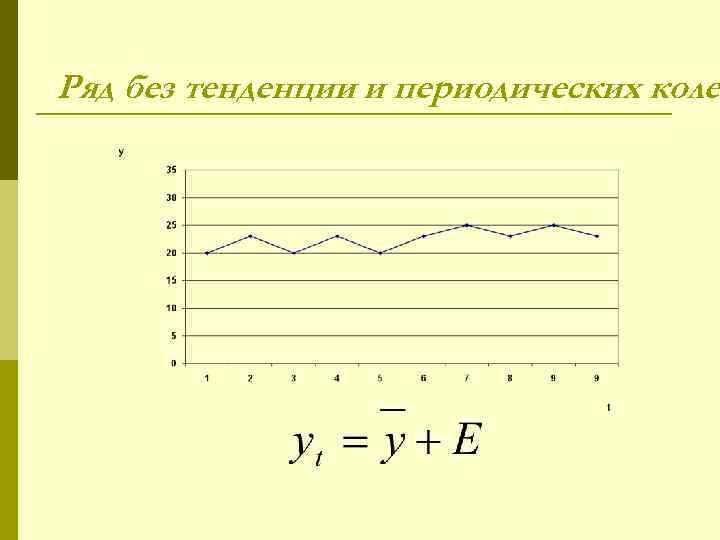
>Ряд без тенденции и периодических коле Ряд без тенденции и периодических коле

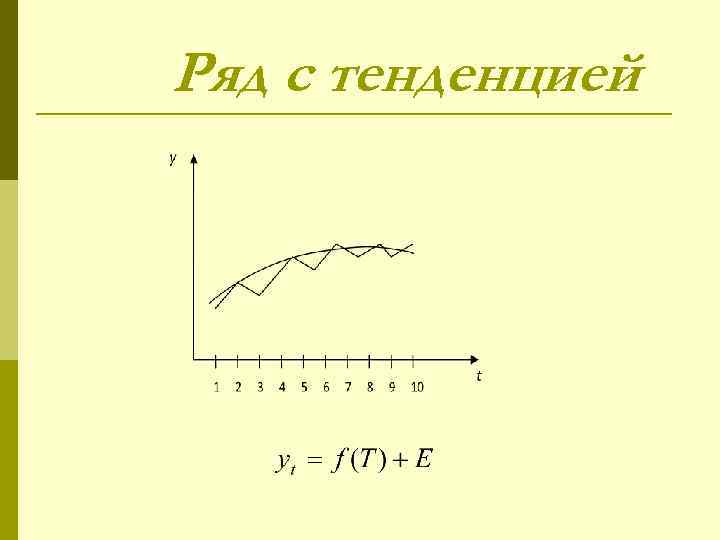
>Ряд с тенденцией Ряд с тенденцией

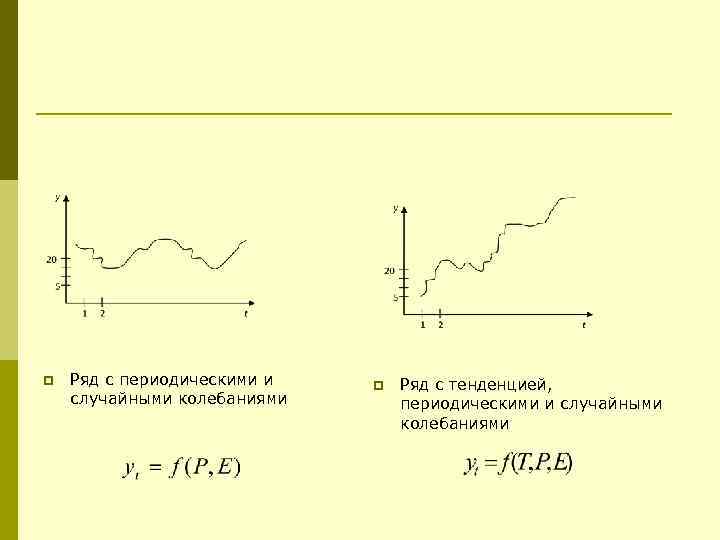
>p Ряд с периодическими и p Ряд с тенденцией, случайными p Ряд с периодическими и p Ряд с тенденцией, случайными колебаниями периодическими и случайными колебаниями

>p. Аддитивная модель p. Мультипликативная модель p. Аддитивная модель p. Мультипликативная модель

>Автокорреляция уровней ряда и ее послед p Корреляционная зависимость между последовательными значениями уровней Автокорреляция уровней ряда и ее послед p Корреляционная зависимость между последовательными значениями уровней временного ряда называется автокорреляцией уровней ряда

> Пример p. Имеются данные о расходах на конечное потребление и Пример p. Имеются данные о расходах на конечное потребление и уровне дохода за 7 промежутков времени в д. е. yt - расходы на потребление, xt- доходы. p t 1 2 3 4 5 6 7 yt 7 8 10 9 11 12 14 xt 12 13 16 15 16 18 19

> Этапы построения модели тенденци (уравнения тренда) p Выбор математической функции, Этапы построения модели тенденци (уравнения тренда) p Выбор математической функции, описывающей тенденцию p Оценка параметров модели p Проверка адекватности выбранной функции и оценка точности модели p Расчет точечного и интервального прогнозов

> Виды математических функций, описывающих тенденцию p Функции с монотонным Виды математических функций, описывающих тенденцию p Функции с монотонным характером возрастания (убывания) и отсутствием пределов роста (снижения) p Кривые с насыщением, т. е. устанавливается нижняя или верхняя граница изменения уровней ряда p S-образные кривые, т. е. кривые с насыщением, имеющие точку перегиба

>Уравнения трендов Уравнения трендов

>Линейный тренд Линейный тренд

>Парабола 2 -го порядка Парабола 2 -го порядка

> Парабола третьей степени p Этот вид тренда предполагает, что по Парабола третьей степени p Этот вид тренда предполагает, что по временному ряду стабильны третьи разности (∆'''), т. е. приросты вторых приростов (∆'''=∆''t - ∆''t-1), а абсолютные ускорения имеют линейную тенденцию

>Показательная функция Показательная функция

> Логарифмическая парабола p Применяется, если стабильны - коэффициенты опережения темпов Логарифмическая парабола p Применяется, если стабильны - коэффициенты опережения темпов роста

>Линеаризация логарифмической парабо Линеаризация логарифмической парабо

> Полулогарифмическая кривая (логарифмический тренд) p Применяется при замедленном росте Полулогарифмическая кривая (логарифмический тренд) p Применяется при замедленном росте уровней временного ряда в конце периода.

> Степенной тренд p При b > 0 она характеризует Степенной тренд p При b > 0 она характеризует непрерывный рост уровней с падающими темпами роста, а при b < 0 – их ускоренное снижение. Величина tb означает базисный коэффициент роста

> Степенной тренд p p - базисный коэффициент роста p Степенной тренд p p - базисный коэффициент роста p - средний коэффициент роста за период

> Кривые с насыщением p Гиперболы – кривые, характеризующие наличие Кривые с насыщением p Гиперболы – кривые, характеризующие наличие асимптоты, выше и ниже которой признак не может принимать значения. p Равносторонняя p Обратная

> Модифицированная экспонента p Характеризуется постоянным отношением последовательных во времени приростов: Модифицированная экспонента p Характеризуется постоянным отношением последовательных во времени приростов:

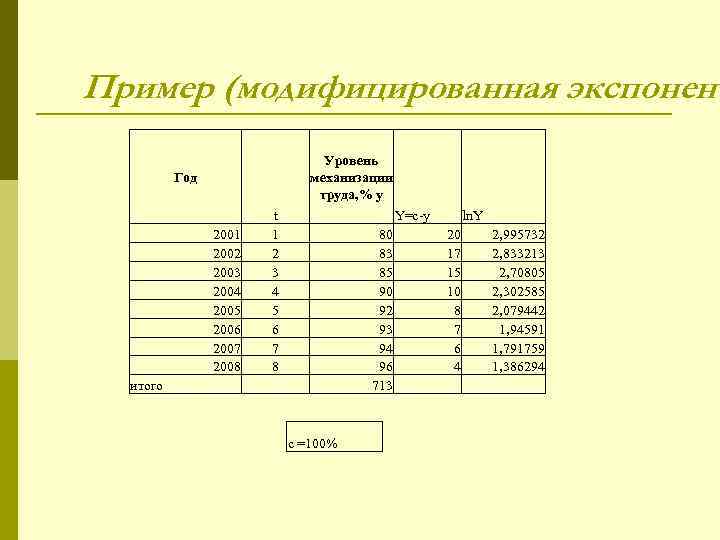
>Пример (модифицированная экспонент Уровень Год Пример (модифицированная экспонент Уровень Год механизации труда, % y t Y=c-y ln. Y 2001 1 80 20 2, 995732 2002 2 83 17 2, 833213 2003 3 85 15 2, 70805 2004 4 90 10 2, 302585 2005 5 92 8 2, 079442 2006 6 93 7 1, 94591 2007 7 94 6 1, 791759 2008 8 96 4 1, 386294 итого 713 c =100%

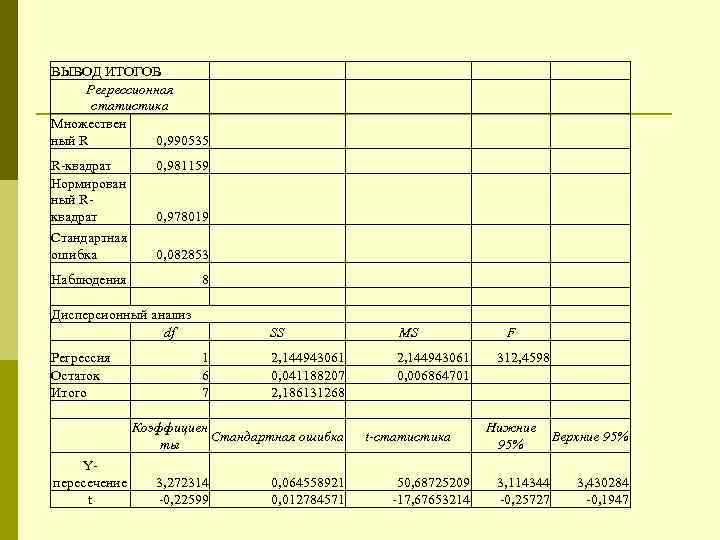
>ВЫВОД ИТОГОВ Регрессионная статистика Множествен ный R 0, 990535 R-квадрат ВЫВОД ИТОГОВ Регрессионная статистика Множествен ный R 0, 990535 R-квадрат 0, 981159 Нормирован ный R- квадрат 0, 978019 Стандартная ошибка 0, 082853 Наблюдения 8 Дисперсионный анализ df SS MS F Регрессия 1 2, 144943061 312, 4598 Остаток 6 0, 041188207 0, 006864701 Итого 7 2, 186131268 Коэффициен Нижние Стандартная ошибка t-статистика Верхние 95% ты 95% Y- пересечение 3, 272314 0, 064558921 50, 68725209 3, 114344 3, 430284 t -0, 22599 0, 012784571 -17, 67653214 -0, 25727 -0, 1947

> ln. Y=lna+tlnb lna=3, 27231 lnb=-0, 22599 ln. Y=lna+tlnb lna=3, 27231 lnb=-0, 22599 a= 26, 3723 b= 0, 797729 Y=26, 3723*0, 7977 t yt=100 -26, 3723*0, 7977 t c =100% 0, 798 - средний коэффициент снижения уровня использования ручного труда за 2001 -2008 гг

>p Приведение к линейному виду модифицированной экспоненты (асимптота с задана исследователем): p Приведение к линейному виду модифицированной экспоненты (асимптота с задана исследователем):

> Логистическая кривая p Подходит для описания такого процесса, при котором изучаемый Логистическая кривая p Подходит для описания такого процесса, при котором изучаемый показатель проходит полный цикл развития, начиная, как правило, от нулевого уровня, сначала медленно, но с ускорением возрастая, затем ускорение становится нулевым в середине цикла (то есть рост происходит по линейному тренду), затем, в завершающей части цикла, рост замедляется по гиперболе по мере приближения к предельному значению показателя.

> Логистическая кривая p c – асимптота Логистическая кривая p c – асимптота

> Логистическая кривая p c – верхняя асимптота Логистическая кривая p c – верхняя асимптота

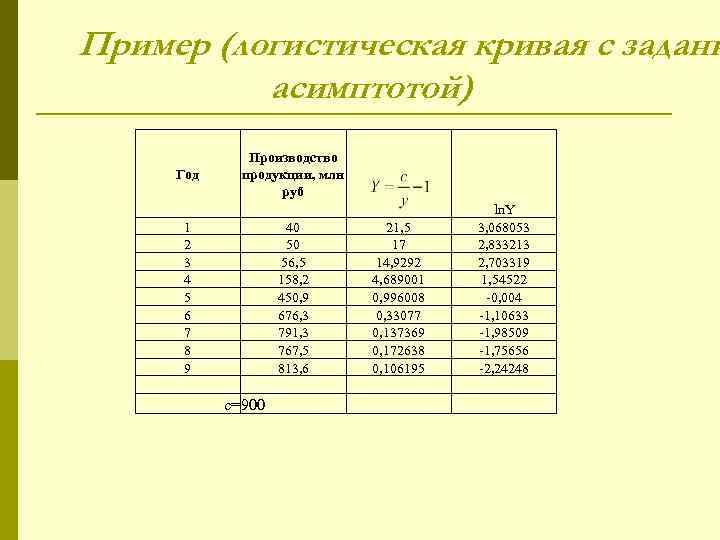
>Пример (логистическая кривая с заданн асимптотой) Производство Год продукции, млн Пример (логистическая кривая с заданн асимптотой) Производство Год продукции, млн руб ln. Y 1 40 21, 5 3, 068053 2 50 17 2, 833213 3 56, 5 14, 9292 2, 703319 4 158, 2 4, 689001 1, 54522 5 450, 996008 -0, 004 6 676, 3 0, 33077 -1, 10633 7 791, 3 0, 137369 -1, 98509 8 767, 5 0, 172638 -1, 75656 9 813, 6 0, 106195 -2, 24248 с=900

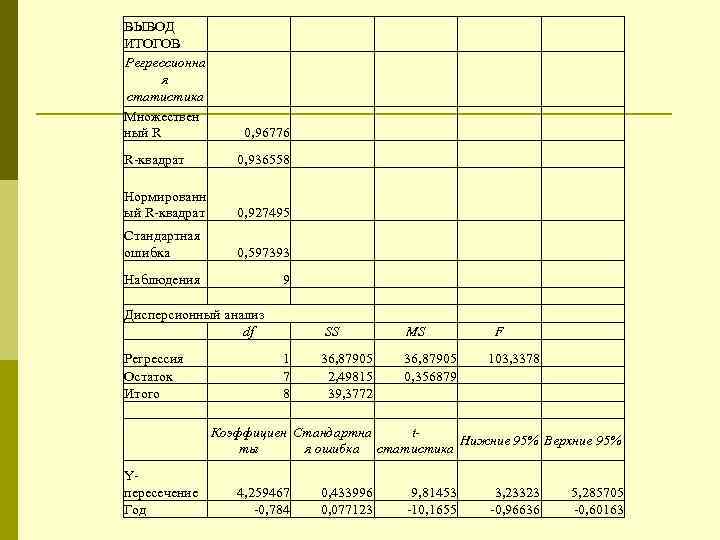
>ВЫВОД ИТОГОВ Регрессионна я статистика Множествен ный R ВЫВОД ИТОГОВ Регрессионна я статистика Множествен ный R 0, 96776 R-квадрат 0, 936558 Нормированн ый R-квадрат 0, 927495 Стандартная ошибка 0, 597393 Наблюдения 9 Дисперсионный анализ df SS MS F Регрессия 1 36, 87905 103, 3378 Остаток 7 2, 49815 0, 356879 Итого 8 39, 3772 Коэффициен Стандартна t- Нижние 95% Верхние 95% ты я ошибка статистика Y- пересечение 4, 259467 0, 433996 9, 81453 3, 23323 5, 285705 Год -0, 784 0, 077123 -10, 1655 -0, 96636 -0, 60163

> Кривая Гомперца–( образная кривая) S p Применяется Кривая Гомперца–( образная кривая) S p Применяется в страховых расчетах, экстраполяции численности населения. p Если с задана, то к линейному виду – при втором логарифмировании

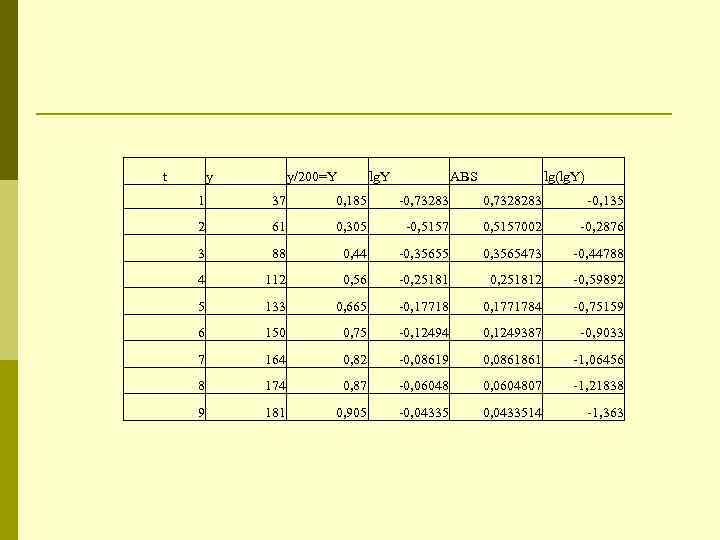
>t y y/200=Y lg. Y ABS t y y/200=Y lg. Y ABS lg(lg. Y) 1 37 0, 185 -0, 73283 0, 7328283 -0, 135 2 61 0, 305 -0, 5157 0, 5157002 -0, 2876 3 88 0, 44 -0, 35655 0, 3565473 -0, 44788 4 112 0, 56 -0, 25181 0, 251812 -0, 59892 5 133 0, 665 -0, 17718 0, 1771784 -0, 75159 6 150 0, 75 -0, 12494 0, 1249387 -0, 9033 7 164 0, 82 -0, 08619 0, 0861861 -1, 06456 8 174 0, 87 -0, 06048 0, 0604807 -1, 21838 9 181 0, 905 -0, 04335 0, 0433514 -1, 363

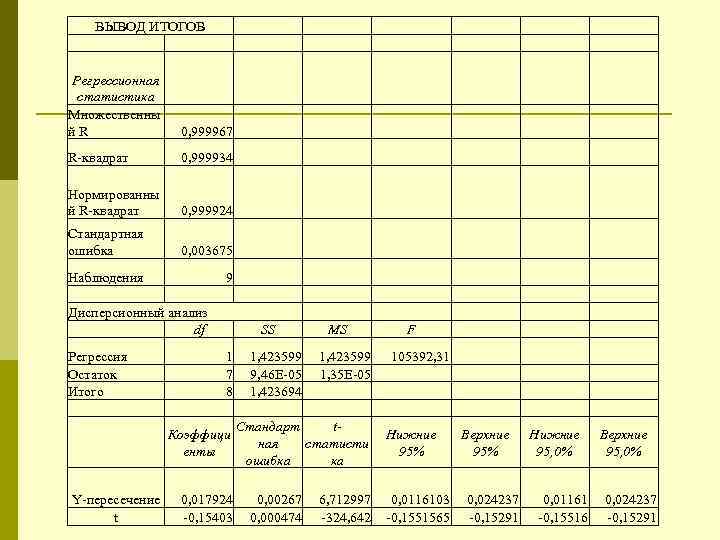
> ВЫВОД ИТОГОВ Регрессионная статистика Множественны й R ВЫВОД ИТОГОВ Регрессионная статистика Множественны й R 0, 999967 R-квадрат 0, 999934 Нормированны й R-квадрат 0, 999924 Стандартная ошибка 0, 003675 Наблюдения 9 Дисперсионный анализ df SS MS F Регрессия 1 1, 423599 105392, 31 Остаток 7 9, 46 E-05 1, 35 E-05 Итого 8 1, 423694 Стандарт t- Коэффици Нижние Верхние Нижние Верхние ная статисти енты 95% 95, 0% ошибка ка Y-пересечение 0, 017924 0, 00267 6, 712997 0, 0116103 0, 024237 0, 01161 0, 024237 t -0, 15403 0, 000474 -324, 642 -0, 1551565 -0, 15291 -0, 15516 -0, 15291

>Использование трендовых моделей д прогнозирования Использование трендовых моделей д прогнозирования

>Моделирование периодических колеб p Ряды могут содержать только периодические колебания p Моделирование периодических колеб p Ряды могут содержать только периодические колебания p Ряды могут содержать и периодические колебания и тенденцию.

>p Для выявления измерения периодических колебаний во временных рядах можно использовать метод p Для выявления измерения периодических колебаний во временных рядах можно использовать метод гармонического анализа ряда. p Сущность метода состоит в представлении функций в виде суммы гармонических колебаний.

> Ряд Фурье p Ряд Фурье -один из методов моделирования временного Ряд Фурье p Ряд Фурье -один из методов моделирования временного ряда с периодическими колебаниями. p Его построение зависит от наличия или отсутствия тенденции в ряду динамики. При отсутствии тенденции, т. е. при стационарном динамическом ряде, методика построения ряда Фурье применяется непосредственно к уровням динамического ряда. p Если же в ряде динамики наблюдается тенденция, то ряд Фурье применяется к отклонениям от тенденции.

>Моделирование периодических колеб p Ряд Фурье можно описать в виде функции: p Моделирование периодических колеб p Ряд Фурье можно описать в виде функции: p Это ряд с двумя гармониками. Могут быть и 3 и 4 гармоники. Чаще всего используется ряд Фурье не более чем с 4 гармониками. p - среднее значение ряда p Параметры определяются с помощью МНК

> Методы исключения тенденции при моделировани взаимосвязей по временным рядам p Метод Методы исключения тенденции при моделировани взаимосвязей по временным рядам p Метод отклонений от тренда p Метод последовательных разностей p Включение в модель регрессии по временным рядам фактора времени

>Метод отклонений от тренда Метод отклонений от тренда

>p - прогнозное значение у p - прогноз у p - прогнозное значение у p - прогноз у по тренду при t=p p - прогнозное значение х p - прогноз х исходя из уравнения тренда при t=p

>Метод последовательных разностей Метод последовательных разностей

>p прогнозное значение уровня ряда p конечный уровень динамического p прогнозное значение уровня ряда p конечный уровень динамического ряда ; p и - то же по ряду

>Включение в модель регрессии по временным фактора времени Включение в модель регрессии по временным фактора времени

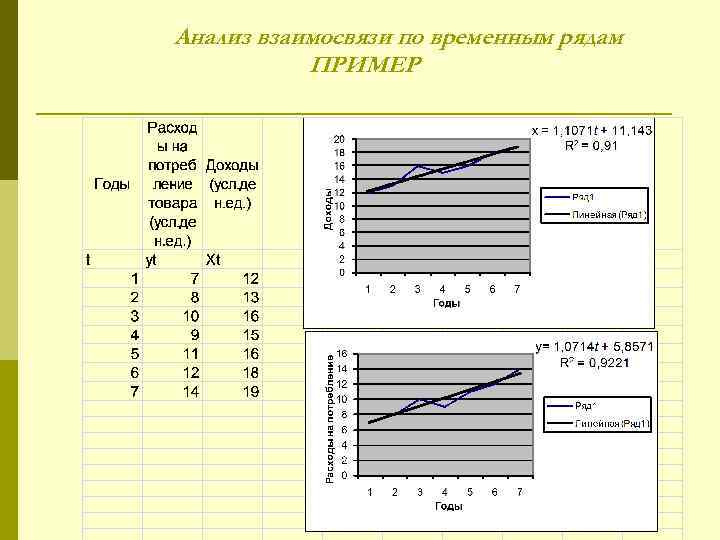
>Анализ взаимосвязи по временным рядам ПРИМЕР Анализ взаимосвязи по временным рядам ПРИМЕР

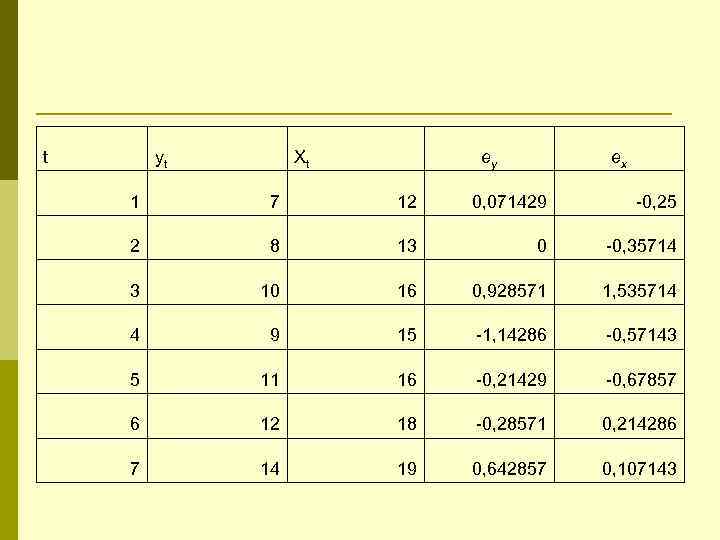
>t yt Xt ey ex 1 t yt Xt ey ex 1 7 12 0, 071429 -0, 25 2 8 13 0 -0, 35714 3 10 16 0, 928571 1, 535714 4 9 15 -1, 14286 -0, 57143 5 11 16 -0, 21429 -0, 67857 6 12 18 -0, 28571 0, 214286 7 14 19 0, 642857 0, 107143

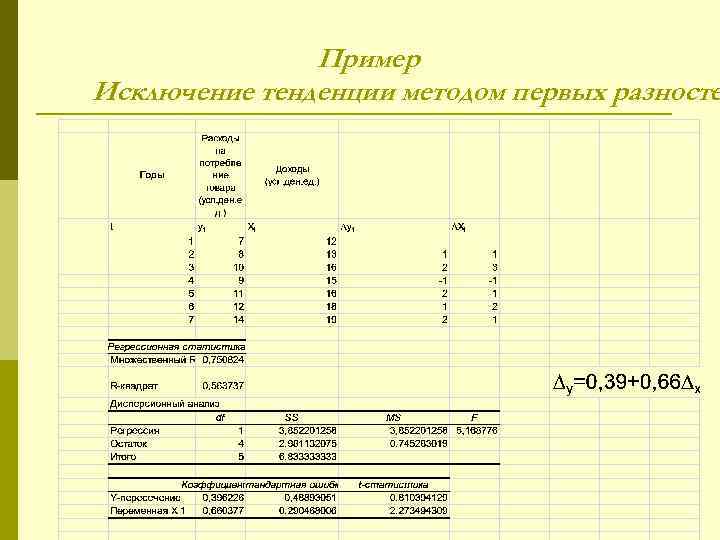
> Пример Исключение тенденции методом первых разносте Пример Исключение тенденции методом первых разносте

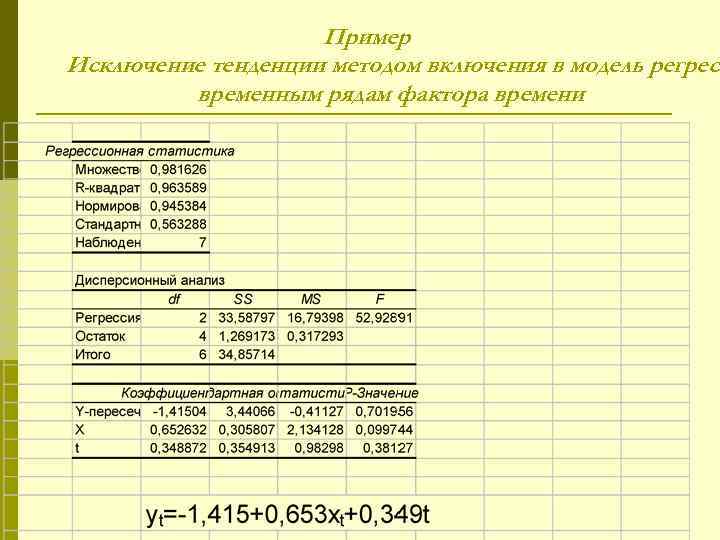
> Пример Исключение тенденции методом включения в модель регресс Пример Исключение тенденции методом включения в модель регресс временным рядам фактора времени

>Автокорреляция в остатках. Критери Дарбина-Уотсона Автокорреляция в остатках. Критери Дарбина-Уотсона

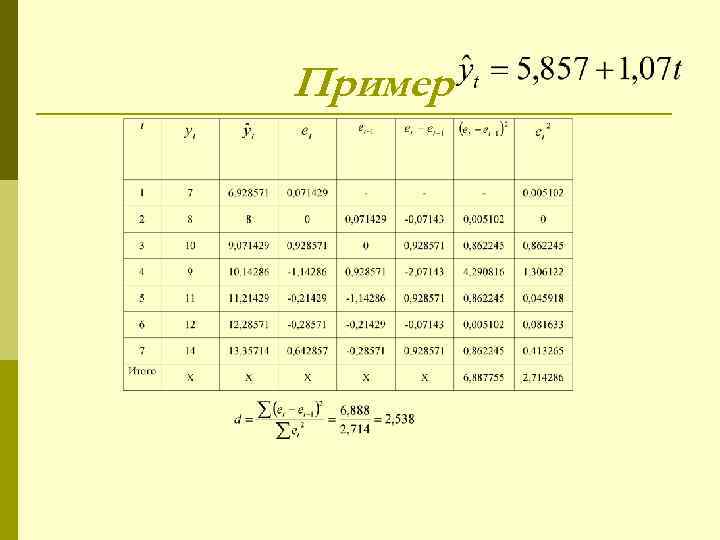
>Пример Пример

>pесть а/к pнет а/к pесть а/к p 0 p dl pесть а/к pнет а/к pесть а/к p 0 p dl p du p 2 p 4 -du p 4 -dl p 4

> Обобщенный метод наименьших квадратов при построении модели регре временным рядам Обобщенный метод наименьших квадратов при построении модели регре временным рядам (ОМНК ) Алгоритм ОМНК 1. Преобразование исходных переменных 2. Применение обычного МНК к уравнению и определение a* и b 3. Расчет параметра a 4. Переход к исходному уравнению

>Поправка Прайса-Винстена Поправка Прайса-Винстена

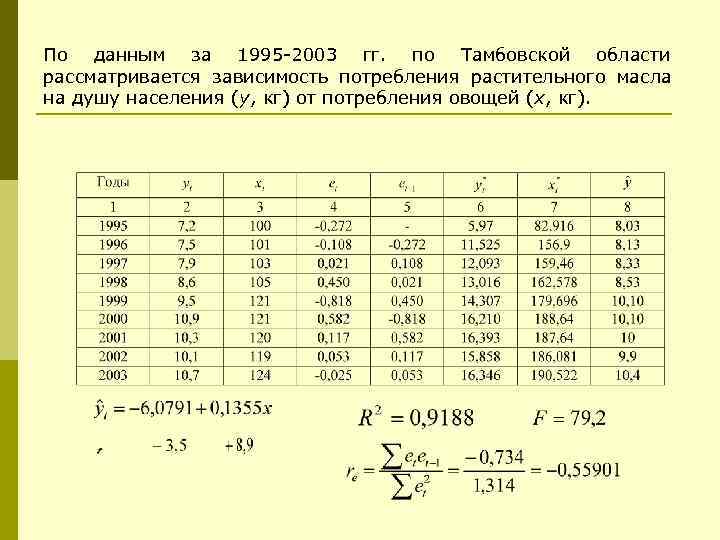
>По данным за 1995 -2003 гг. по Тамбовской области рассматривается зависимость потребления растительного По данным за 1995 -2003 гг. по Тамбовской области рассматривается зависимость потребления растительного масла на душу населения (y, кг) от потребления овощей (x, кг).

> Расчет преобразованных значений p и т. д. Расчет преобразованных значений p и т. д.

>Учет сезонности при построении мод регрессии p z 1 = 1 Учет сезонности при построении мод регрессии p z 1 = 1 – для первого квартала, p 0 – для остальных; p z 2 = 1 – для второго квартала, p 0 – для остальных; p z 3 = 1 – для третьего квартала, p 0 – для остальных.

>p для I квартала p для II квартала p для p для I квартала p для II квартала p для IV квартала

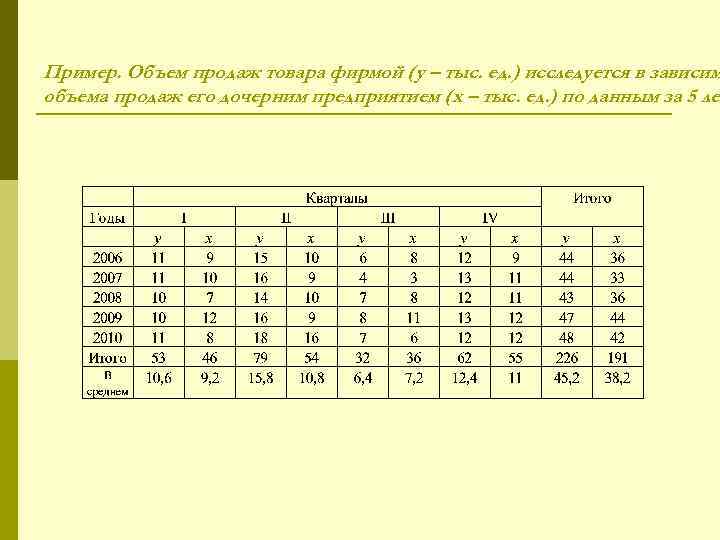
>Пример. Объем продаж товара фирмой (у – тыс. ед. ) исследуется в зависим объема Пример. Объем продаж товара фирмой (у – тыс. ед. ) исследуется в зависим объема продаж его дочерним предприятием (х – тыс. ед. ) по данным за 5 лет

> Моделирование сезонных колебаний p Аддитивная модель p Мультипликативная модель Моделирование сезонных колебаний p Аддитивная модель p Мультипликативная модель p Приблизительно равная сезонная вариация указывает на существование аддитивной модели. p Усиление сезонной вариации с возрастанием тренда указывает на существование мультипликативной модели.

>Построение аддитивной модели Построение аддитивной модели

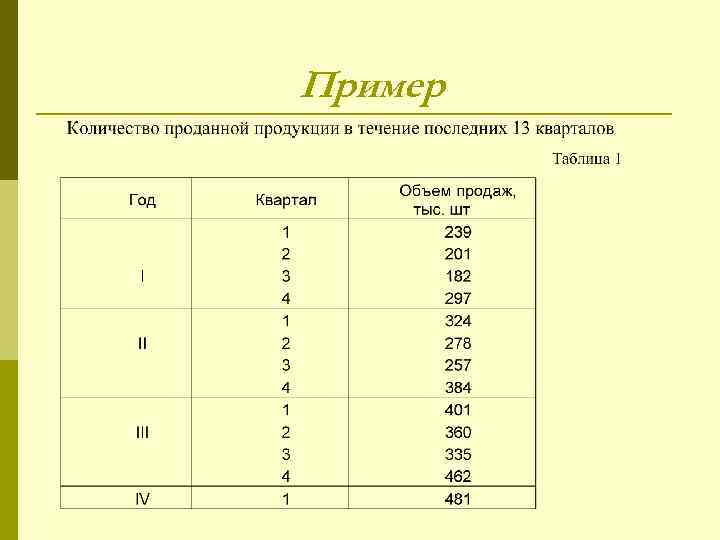
>Пример Пример

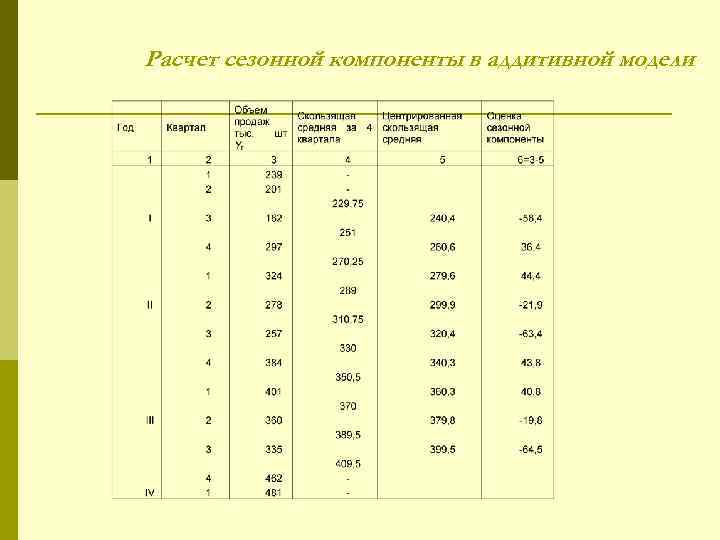
>Расчет сезонной компоненты в аддитивной модели Расчет сезонной компоненты в аддитивной модели

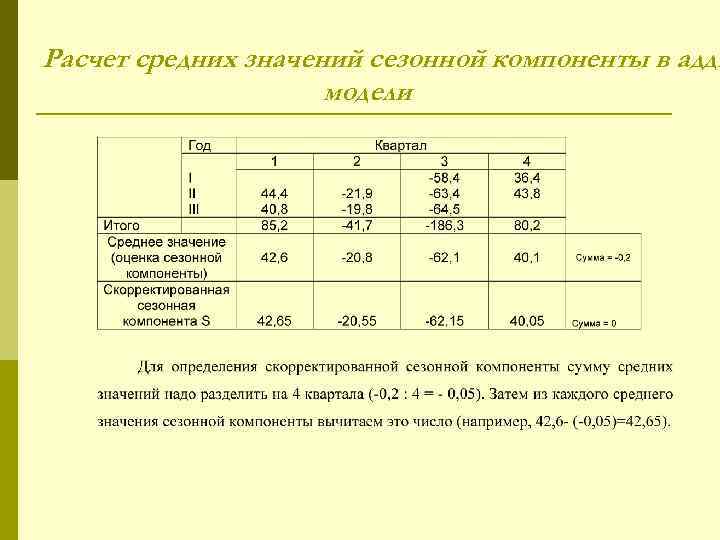
>Расчет средних значений сезонной компоненты в адди модели Расчет средних значений сезонной компоненты в адди модели

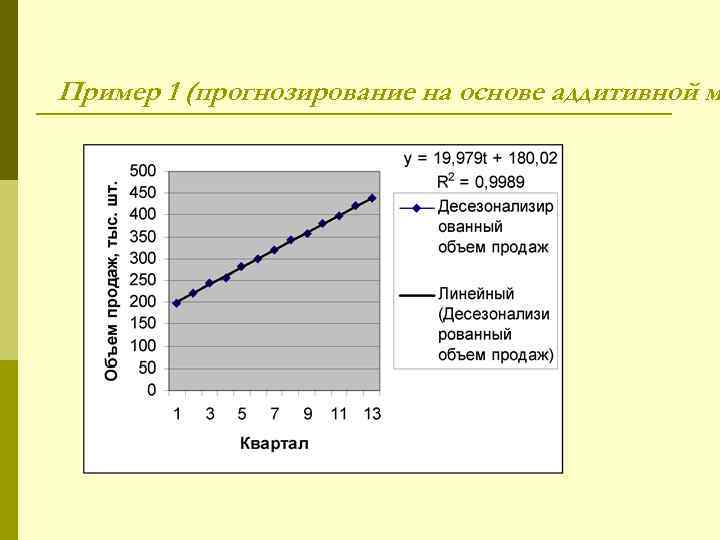
>Пример 1 (прогнозирование на основе аддитивной м Пример 1 (прогнозирование на основе аддитивной м

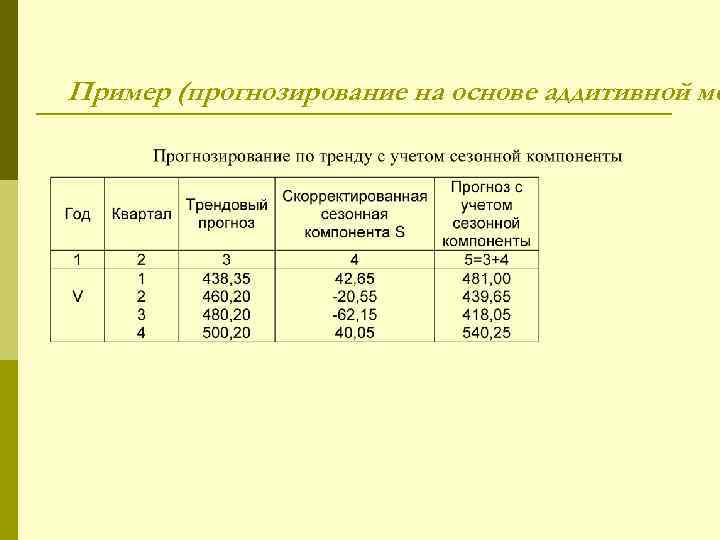
>Пример (прогнозирование на основе аддитивной мо Пример (прогнозирование на основе аддитивной мо

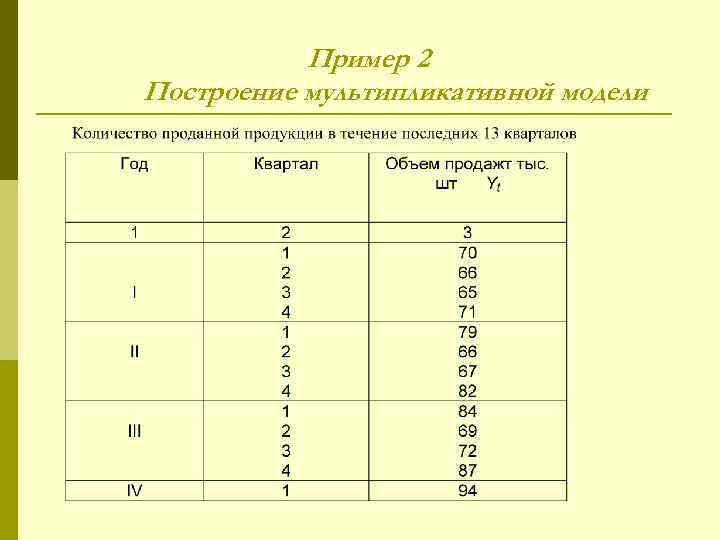
> Пример 2 Построение мультипликативной модели Пример 2 Построение мультипликативной модели

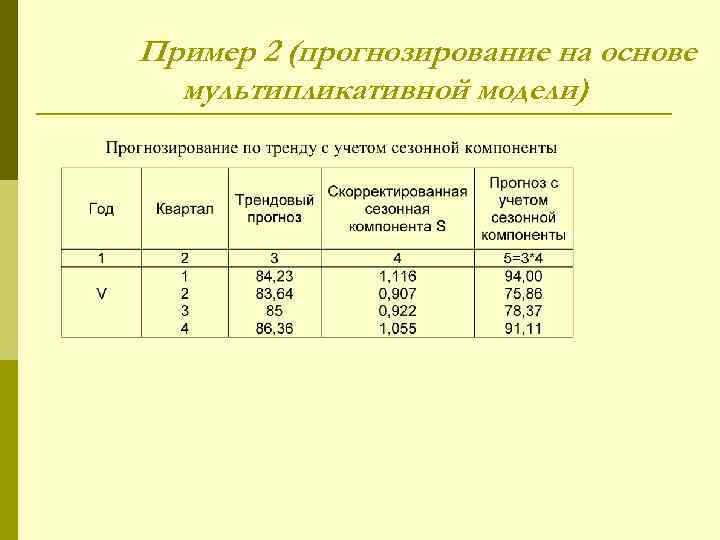
>Пример 2 (прогнозирование на основе мультипликативной модели) Пример 2 (прогнозирование на основе мультипликативной модели)

> МОДЕЛИ С ЛАГОВЫМИ ПЕРЕМЕННЫМИ p 1) модели с лаговыми МОДЕЛИ С ЛАГОВЫМИ ПЕРЕМЕННЫМИ p 1) модели с лаговыми объясняющими переменными или иначе модели с распределенными лагами p 2) модели с лаговыми зависимыми переменными – модели авторегрессии p 3) модели с лаговыми зависимыми и независимыми переменными, т. е. авторегрессионные модели с распределенными лагами

> Модель с распределенными лагами p Данная модель означает, что изменение во Модель с распределенными лагами p Данная модель означает, что изменение во времени t объясняющей переменный x будет влиять на значения результативного признака y в течение 4 -х следующих моментов времени

>p Коэффициент - краткосрочный мультипликатор. Он характеризует среднее изменение результата y при изменении p Коэффициент - краткосрочный мультипликатор. Он характеризует среднее изменение результата y при изменении на 1 единицу своего измерения в фиксированный момент времени t. p В момент времени t+1 воздействие объясняющей переменной x на результат y составит ( ) единиц, а в момент времени t+2 общее изменение y составит ( ) единиц.

> Промежуточные мультипликаторы p при k=4: p Промежуточные мультипликаторы p при k=4: p - изменение y в момент времени t+1; p - изменение y в момент времени t+2; p - изменение y в момент времени t+3.

>p Долгосрочный мультипликатор p При k=4 долгосрочный мультипликатор составит p p Долгосрочный мультипликатор p При k=4 долгосрочный мультипликатор составит p Он характеризует общее среднее изменение y через 4 временных интервала при увеличении x в момент времени t на 1 единицу

> Относительные коэффициенты модели p Характеризует долю общего изменения y Относительные коэффициенты модели p Характеризует долю общего изменения y в момент времени t+j.

> Средняя величина лага p Показывает средний интервал времени, в Средняя величина лага p Показывает средний интервал времени, в течение которого будет происходить изменение зависимой переменной y под воздействием изменения объясняющей переменной x в момент времени t. p Чем меньше величина среднего лага, тем быстрее реагирует результат y на изменение x. И наоборот, высокое значение среднего лага показывает, что воздействие объясняющей переменной на результат будет сказываться с течением длительного промежутка времени.

> Медианный лаг p тот период времени, в течение которого с момента Медианный лаг p тот период времени, в течение которого с момента времени t будет реализована половина общего эффекта воздействия объясняющей переменной x на результат y.

> Пример p где t – время в годах, y Пример p где t – время в годах, y - основные производственные фонды ( млн. руб. ), p x - размер инвестиций (млн. руб. )

>p Рост инвестиций на 1 млн. руб. в текущем периоде приводит к росту p Рост инвестиций на 1 млн. руб. в текущем периоде приводит к росту основных производственных фондов: p - в том же периоде на 0, 7 млн. руб. (краткосрочный мультипликатор); p - через 1 год на 0, 7+1=1, 7 млн. руб. ; p - через 2 года на 0, 7+1+1, 5=3, 2 млн. руб. ; p - через 3 года на 3, 8 млн. руб. (промежуточный, как и предыдущие два, мультипликатор); p - через 4 года на 4 млн. руб. (долгосрочный мультипликатор).

>p Относительные коэффициенты модели: p = 0, 7 / 4 = p Относительные коэффициенты модели: p = 0, 7 / 4 = 0, 175; p = 1 / 4 = 0, 25; p = 1, 5 / 4 = 0, 375; p = 0, 6 / 4 = 0, 15; p = 0, 2 / 4 = 0, 05. p В текущем году реализуется 17, 5% воздействия увеличения инвестиций на рост основных производственных фондов, а через год еще 25%. Через 2 года – еще 37, 5%, через 3 года – еще 15% и через 4 года – еще 5%.