Вписані і центральні кути ПОДУМАЙТЕ

Вписані і центральні кути

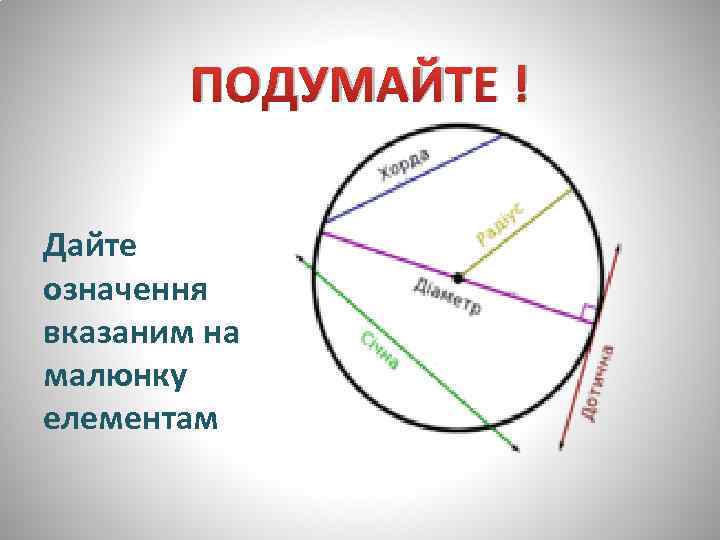ПОДУМАЙТЕ ! Дайте означення вказаним на малюнку елементам

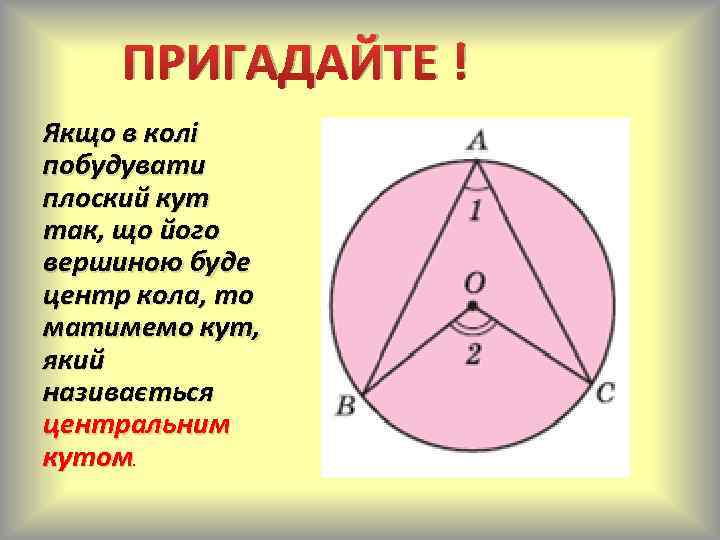ПРИГАДАЙТЕ ! Якщо в колі побудувати плоский кут так, що його вершиною буде центр кола, то матимемо кут, який називається центральним кутом.

Частина кола, яка знаходиться всередині плоского кута, називається дугою кола. Градусна міра дуги кола — це градусна міра відповідного центрального кута. О А В

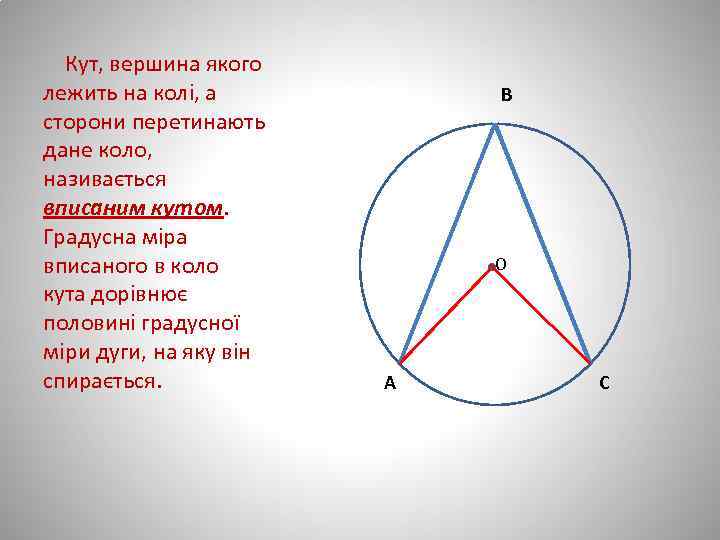Кут, вершина якого лежить на колі, а сторони перетинають дане коло, називається вписаним кутом. Градусна міра вписаного в коло кута дорівнює половині градусної міри дуги, на яку він спирається. В ОООООО А С

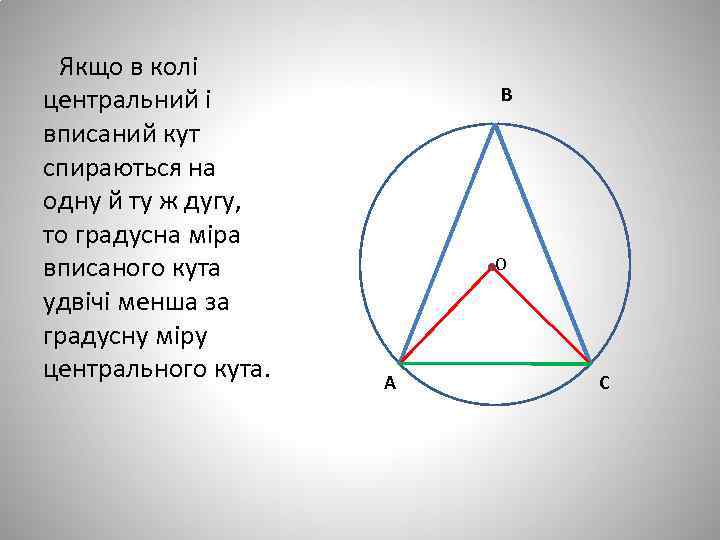Якщо в колі центральний і вписаний кут спираються на одну й ту ж дугу, то градусна міра вписаного кута удвічі менша за градусну міру центрального кута. В ОООООО А С

Увага! Проводимо дослідження

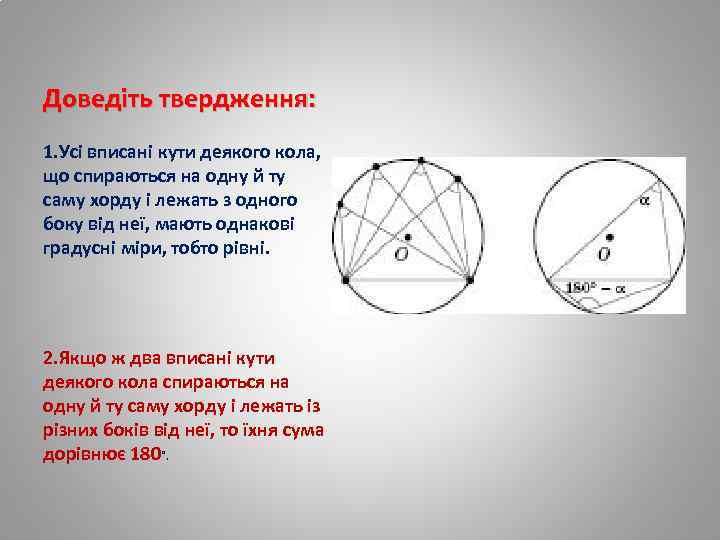Доведіть твердження: 1. Усі вписані кути деякого кола, що спираються на одну й ту саму хорду і лежать з одного боку від неї, мають однакові градусні міри, тобто рівні. 2. Якщо ж два вписані кути деякого кола спираються на одну й ту саму хорду і лежать із різних боків від неї, то їхня сума дорівнює 180°.

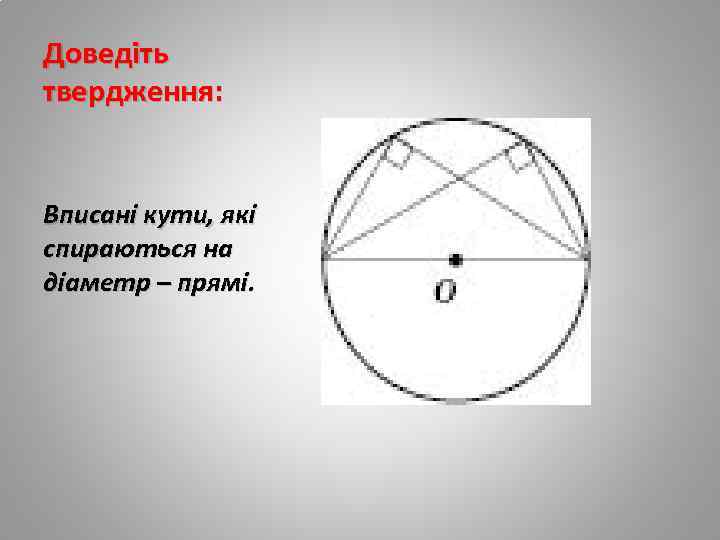Доведіть твердження: Вписані кути, які спираються на діаметр – прямі.

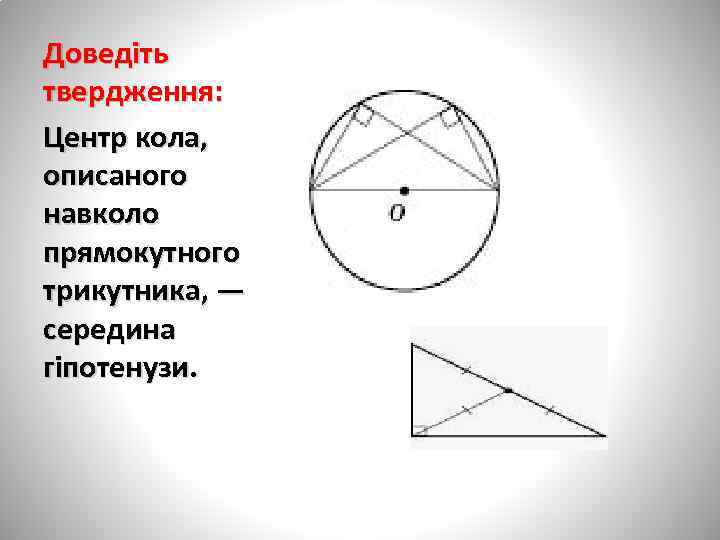Доведіть твердження: Центр кола, описаного навколо прямокутного трикутника, — середина гіпотенузи.

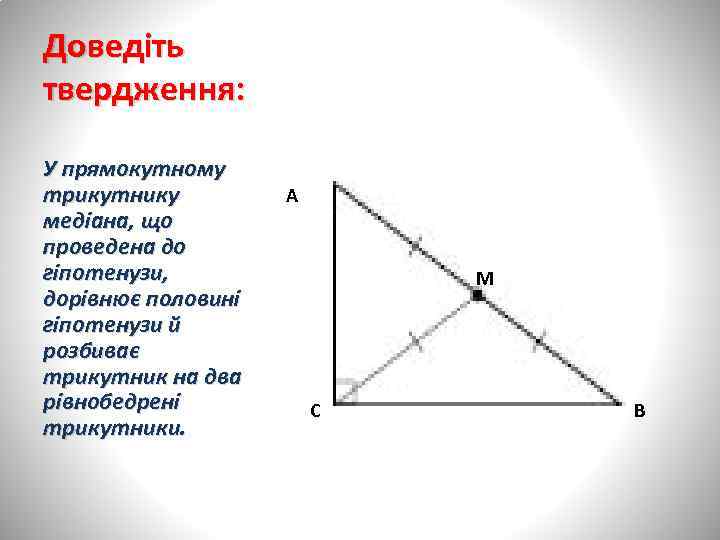Доведіть твердження: У прямокутному трикутнику медіана, що проведена до гіпотенузи, дорівнює половині гіпотенузи й розбиває трикутник на два рівнобедрені трикутники. А М С В

Розв´яжіть задачу: 1. Трикутник ABC вписаний у коло, центр якого лежить на відрізку АВ. а) Знайдіть кут В, якщо A = 65°. б) Знайдіть медіану, проведену з вершини С, якщо АВ = 12 см. 2. На колі позначено точки А, В і С, при чому. АС — діаметр кола, кут. BCA = 60°, ВС = 4 см. Знайдіть радіус кола. 3* (опорна). Кут між хордою і дотичною до кола, проведеною через кінець хор ди, вимірюється половиною дуги, яка лежить усередині цього кута. Доведіть. 4* (опорна), а) Дуги кола, які містяться між двома паралельними хор дами, рівні. Доведіть, б) Рівні хорди стягують дуги з однаковою гра дусною мірою, і навпаки: дуги з однаковою градусною мірою стягуються рівними хордами. Доведіть.

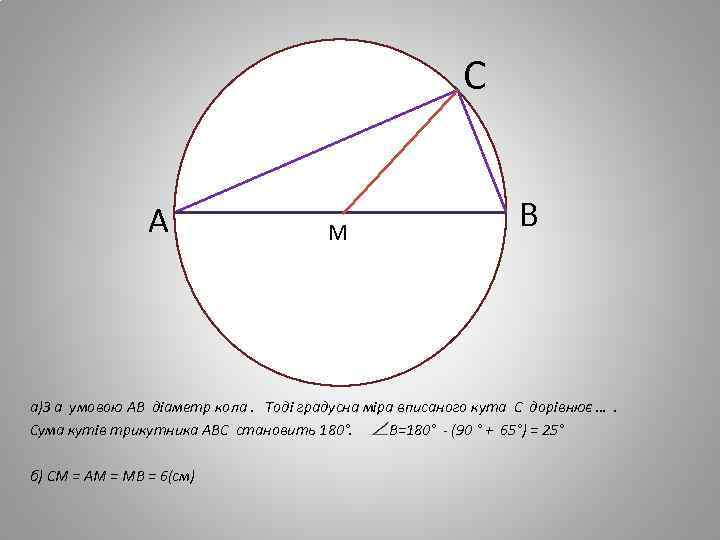С А М В а)З а умовою АВ діаметр кола. Тоді градусна міра вписаного кута С дорівнює …. Сума кутів трикутника АВС становить 180°. В=180° - (90 ° + 65°) = 25° б) СМ = АМ = МВ = 6(см)

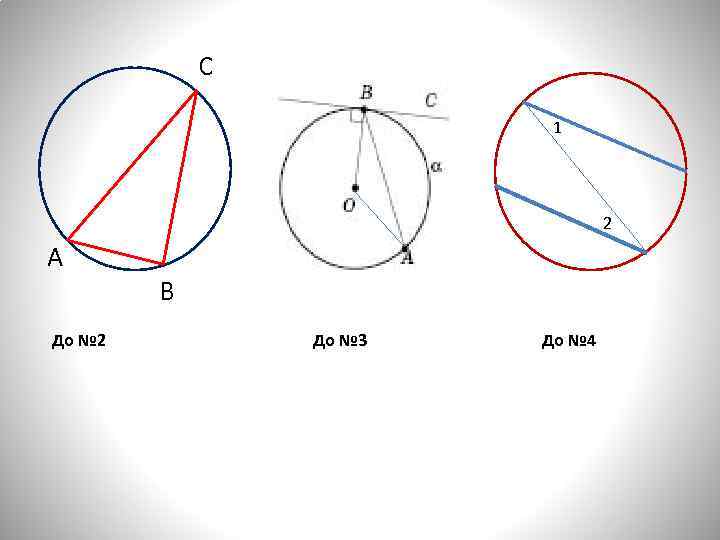С 1 2 А В До № 2 До № 3 До № 4

Т Е С Т Вписані кути

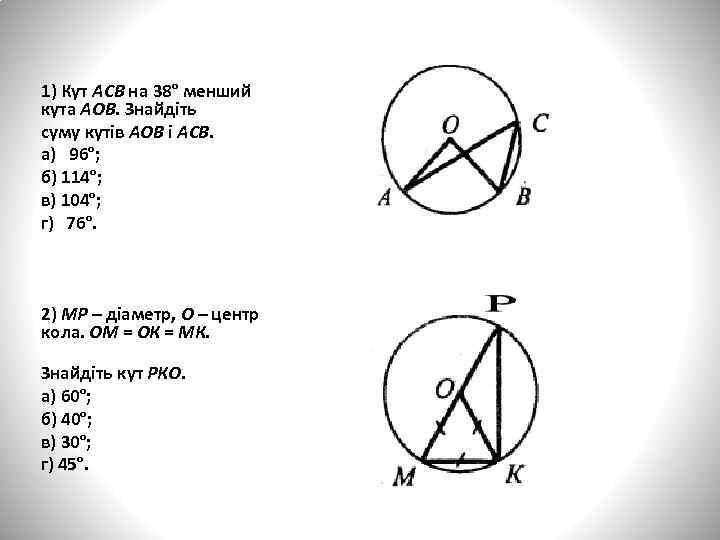1) Кут АСВ на 38° менший кута АОВ. Знайдіть суму кутів АОВ і АСВ. а) 96°; б) 114°; в) 104°; г) 76°. 2) МР – діаметр, О – центр кола. ОМ = ОК = МК. Знайдіть кут РКО. а) 60°; б) 40°; в) 30°; г) 45°.

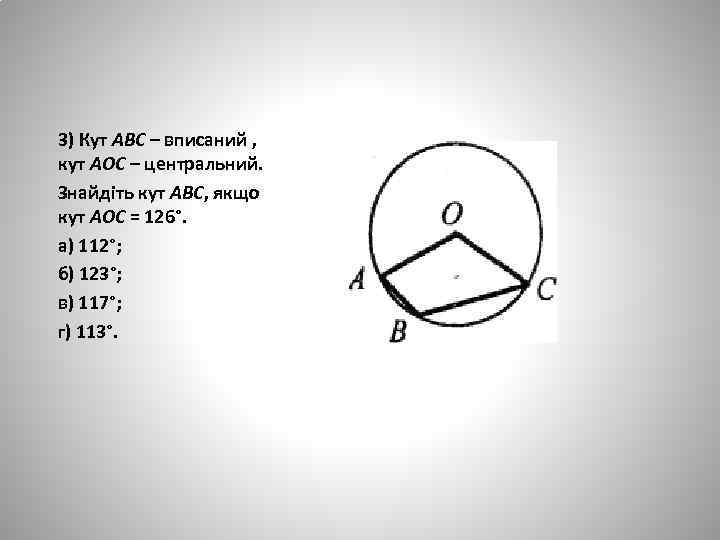3) Кут АВС – вписаний , кут АОС – центральний. Знайдіть кут АВС, якщо кут АОС = 126°. а) 112°; б) 123°; в) 117°; г) 113°.

Відповіді: 1 - Б; 2 - В; 3 - В.