Вписане та описане коло
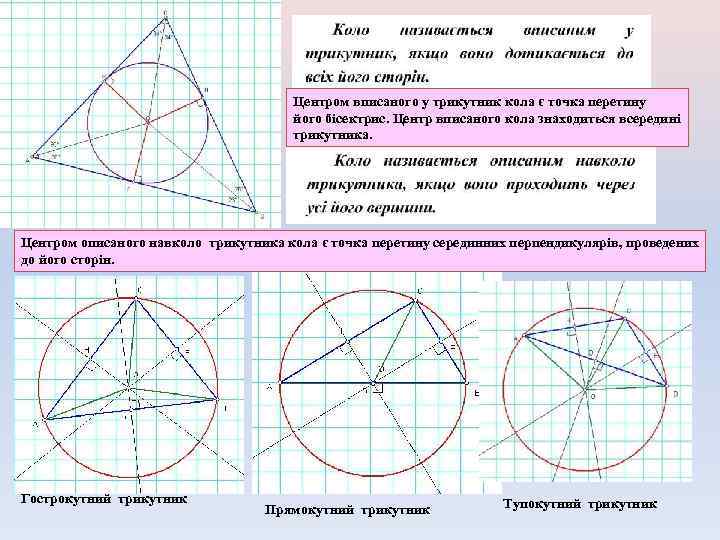Центром вписаного у трикутник кола є точка перетину його бісектрис. Центр вписаного кола знаходиться всередині трикутника. Центром описаного навколо трикутника кола є точка перетину серединних перпендикулярів, проведених до його сторін. Гострокутний трикутник Прямокутний трикутник Тупокутний трикутник
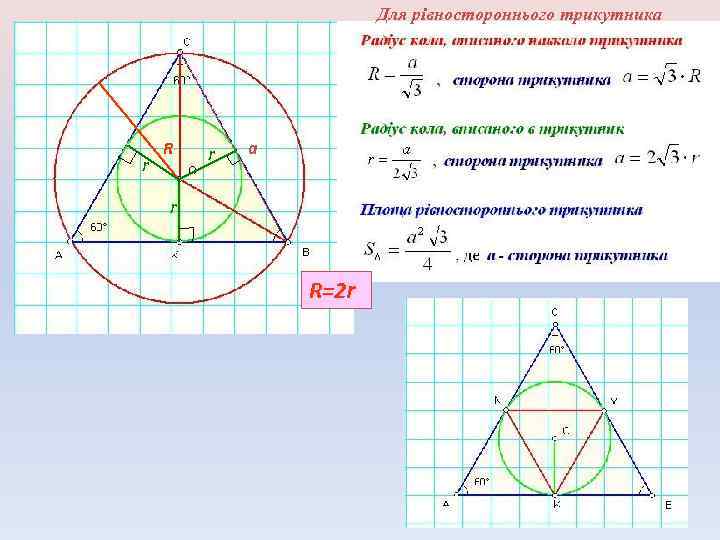Для рівностороннього трикутника r R r a r R=2 r
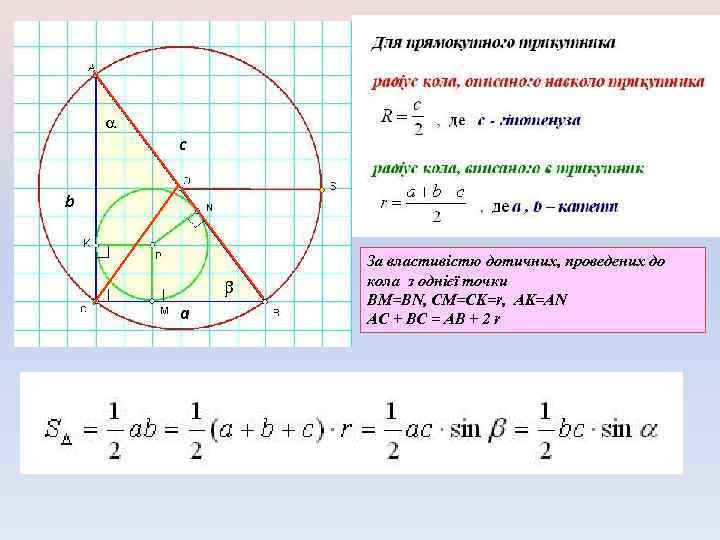c b a За властивістю дотичних, проведених до кола з однієї точки BM=BN, CM=CK=r, AK=AN AC + BC = AB + 2 r
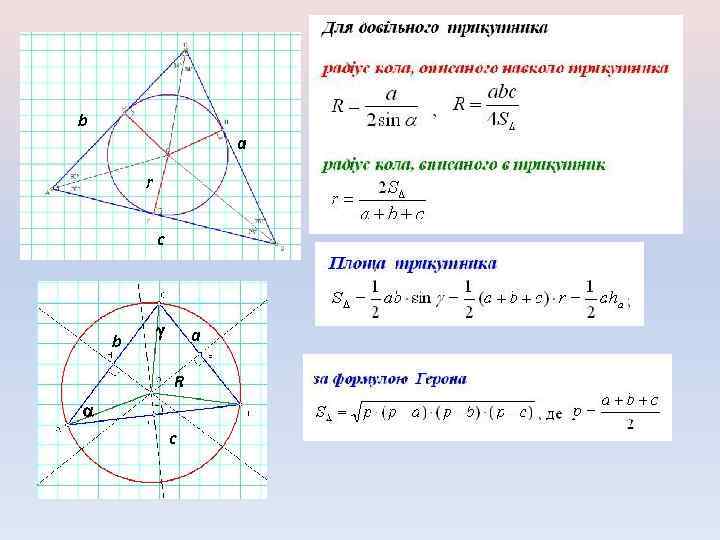b a r c b a R c
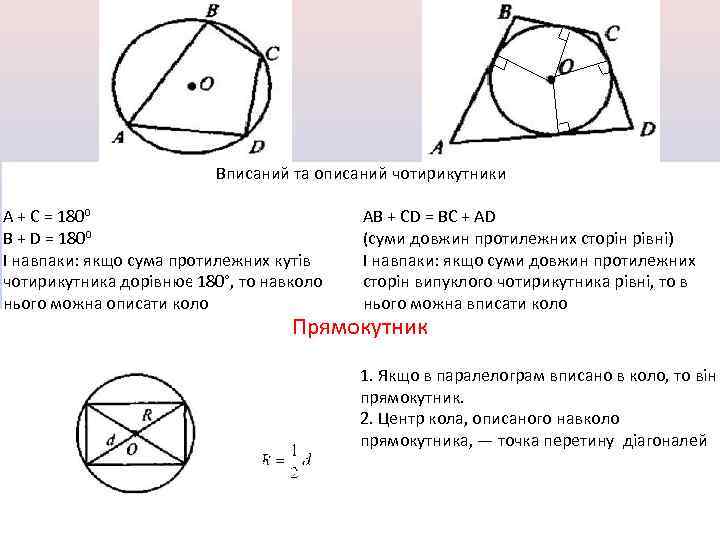Вписаний та описаний чотирикутники A + C = 180⁰ B + D = 180⁰ І навпаки: якщо сума протилежних кутів чотирикутника дорівнює 180°, то навколо нього можна описати коло AB + CD = BC + AD (суми довжин протилежних сторін рівні) І навпаки: якщо суми довжин протилежних сторін випуклого чотирикутника рівні, то в нього можна вписати коло Прямокутник 1. Якщо в паралелограм вписано в коло, то він прямокутник. 2. Центр кола, описаного навколо прямокутника, — точка перетину діагоналей
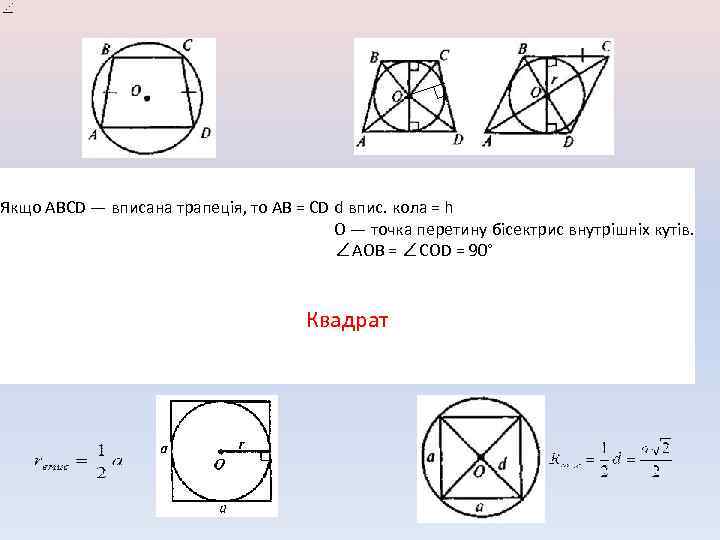Якщо ABCD — вписана трапеція, то AB = CD d впиc. кола = h O — точка перетину бісектрис внутрішніх кутів. ∠AOB = ∠COD = 90° Квадрат
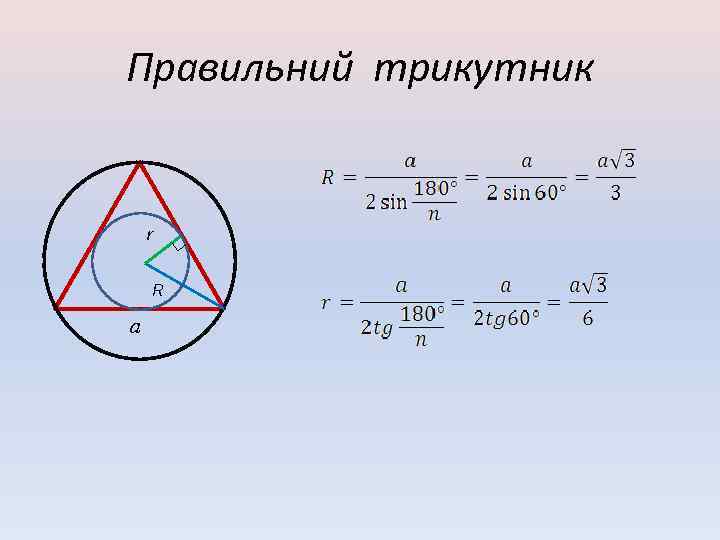Правильний трикутник r R a
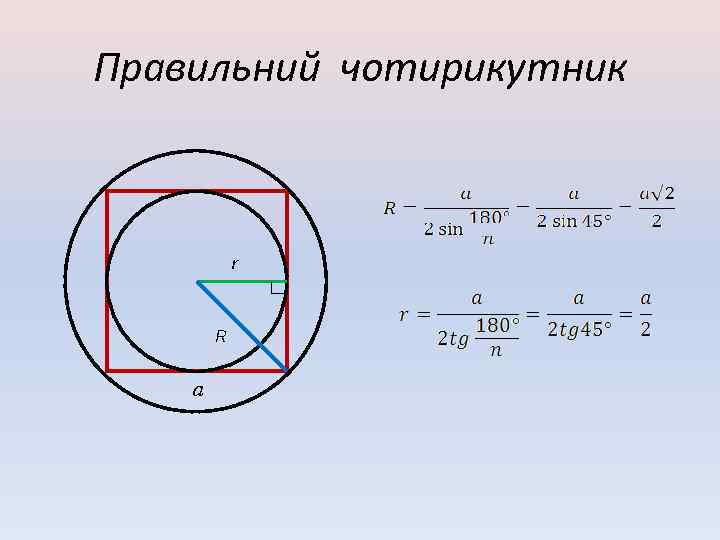Правильний чотирикутник r R a
Правильний шестикутник R r a