Возможности построения следующих типов графиков: § Линейный (в

Возможности построения следующих типов графиков: § Линейный (в прямоугольных и полярных координатах; § Линии уровня поверхности; § Поверхность; § Столбиковая диаграмма; § Точечный и векторный графики поверхности

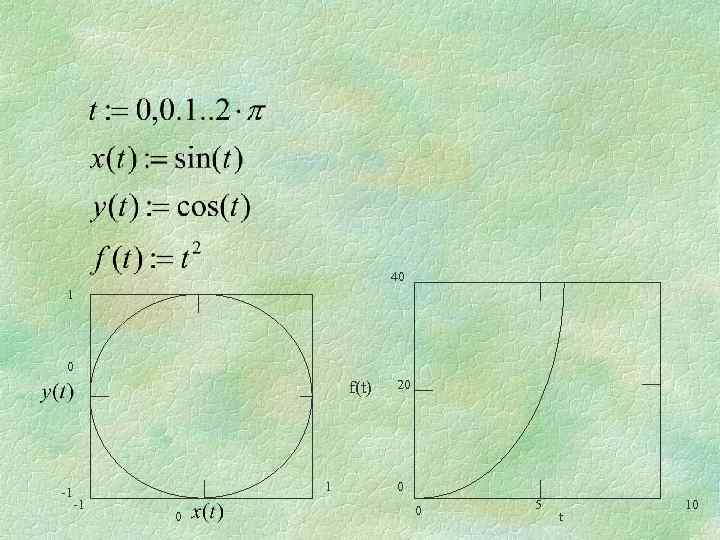40 1 0 f(t) -1 1 -1 0 20 0 0 5 t 10

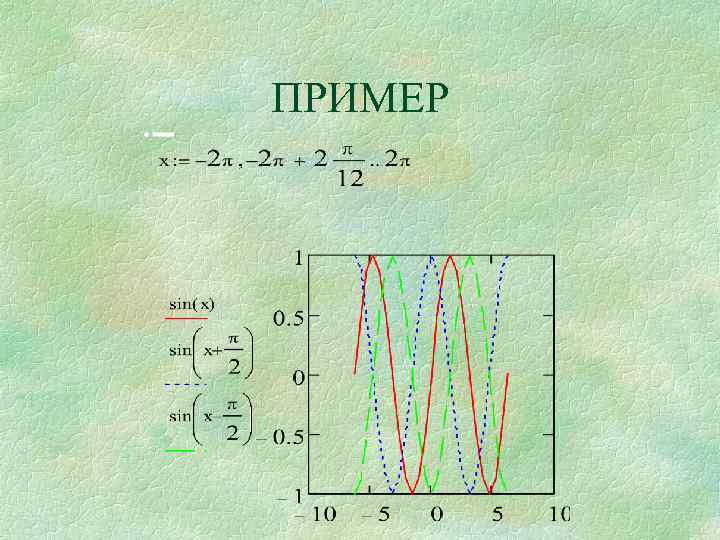ПРИМЕР

Решение задач нецелочисленной оптимизации Задача нецелочисленной оптимизации состоит в том, чтобы подобрать такие значения аргументов целевой функции, при которых данная функция принимает экстремальное (минимальное или максимальное) значение и соблюдается заданная система ограничений на значения аргументов

В математической форме задача может быть сформулирована следующим образом: Где: f- целевая функция; n- количество аргументов целевой функции; - элементы системы ограничений (равенств или неравенств различного вида k - количество ограничений

ПРИМЕР Математическая задача запишется следующим образом:

В системе Math. Cad такие задачи решаются с помощью блоков Given-Maximize и Given. Minimize Решающий блок состоит из нескольких компонент, следующих на листе в строго определенном порядке: 1. Присваивание начальных значений переменным, относительно которых решается задача оптимизации. 2. Определение целевой функции. 3. Директива Given. 4. Ограничения, записываемые в обычной математической форме. 5. Обращение к одной из функций Maximize или Minimize.

Решение задачи о студенте в системе Мath. Cad