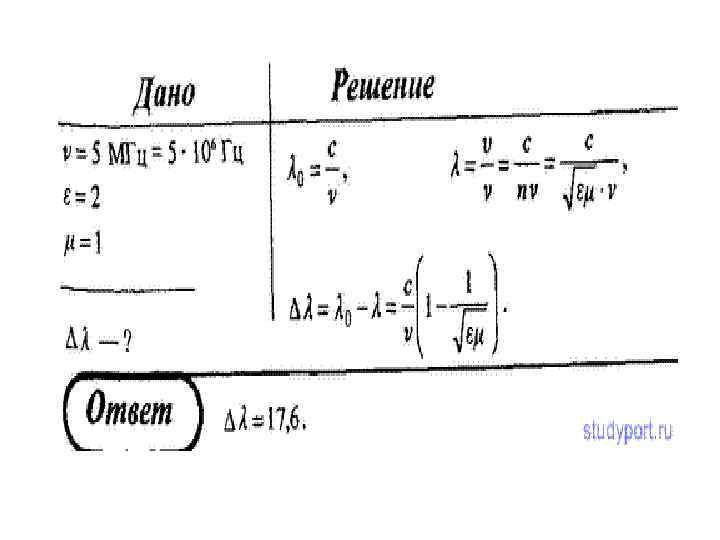
ВОУД. Электромагнетизм
ВОУД. Электромагнетизм
 (F) ( E ) (C) • Одноименные заряды отталкиваются, разноименные притягиваются • Существуют два рода электрических зарядов, условно названных положительными и отрицательными • Заряды могут передаваться от одного тела к другому
(F) ( E ) (C) • Одноименные заряды отталкиваются, разноименные притягиваются • Существуют два рода электрических зарядов, условно названных положительными и отрицательными • Заряды могут передаваться от одного тела к другому
 (A) ( C ) ( G ) • В окружающем пространстве создается любым заряженным телом • Оказывается силовое действие на другие заряженные тела • Действует на электрические заряды с некоторой силой
(A) ( C ) ( G ) • В окружающем пространстве создается любым заряженным телом • Оказывается силовое действие на другие заряженные тела • Действует на электрические заряды с некоторой силой
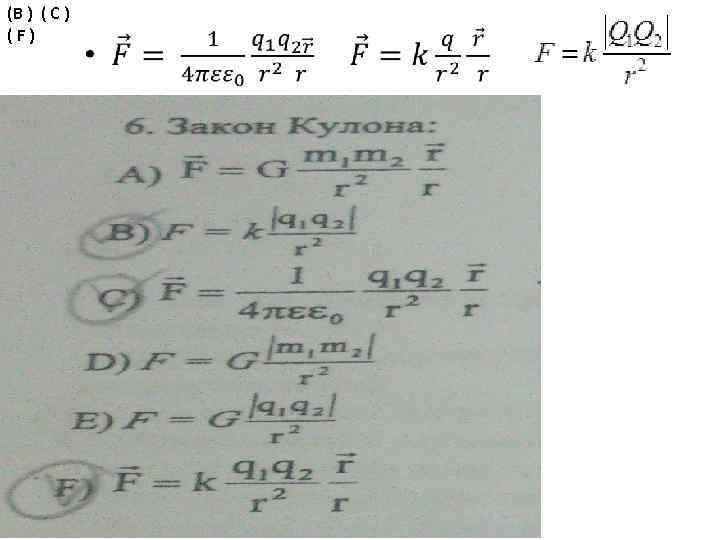 (B ) ( C ) ( F ) •
(B ) ( C ) ( F ) •
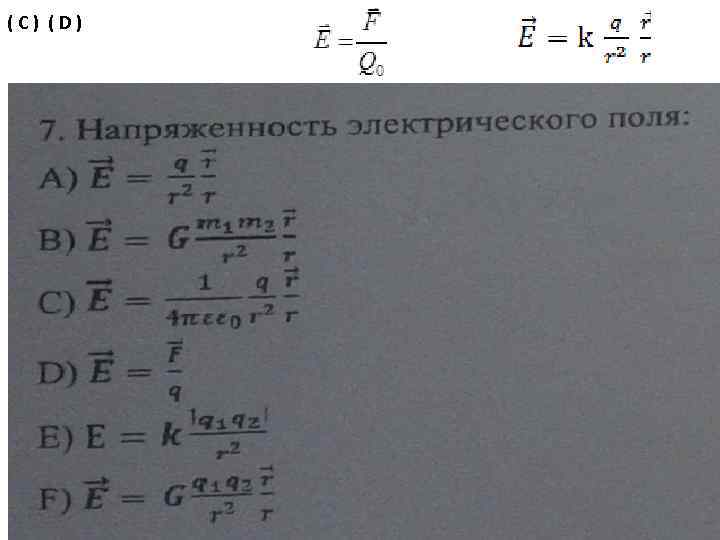 ( C ) ( D )
( C ) ( D )
 (C ) (D) •
(C ) (D) •
 ( Е ) ɛ
( Е ) ɛ
 ( A ) (B )
( A ) (B )
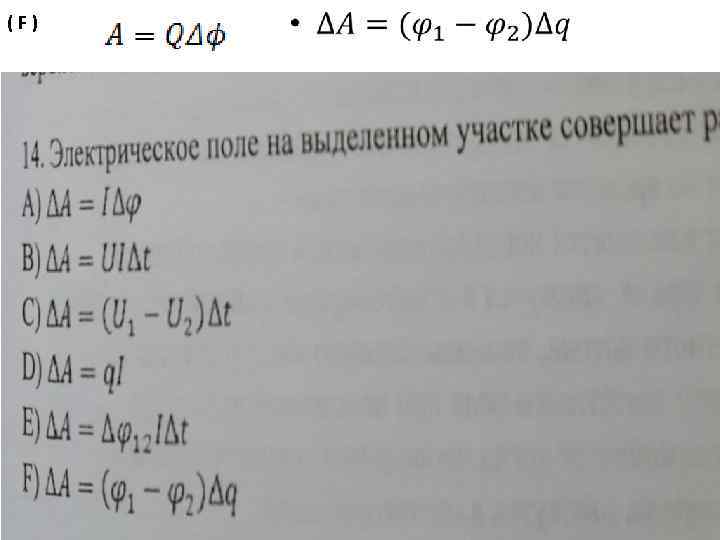 ( F ) •
( F ) •
 ( C ) (E ) •
( C ) (E ) •
 ( D ) ( Е ) •
( D ) ( Е ) •
 ( С ) ( Е ) (А ) Вектор электрического смещения
( С ) ( Е ) (А ) Вектор электрического смещения
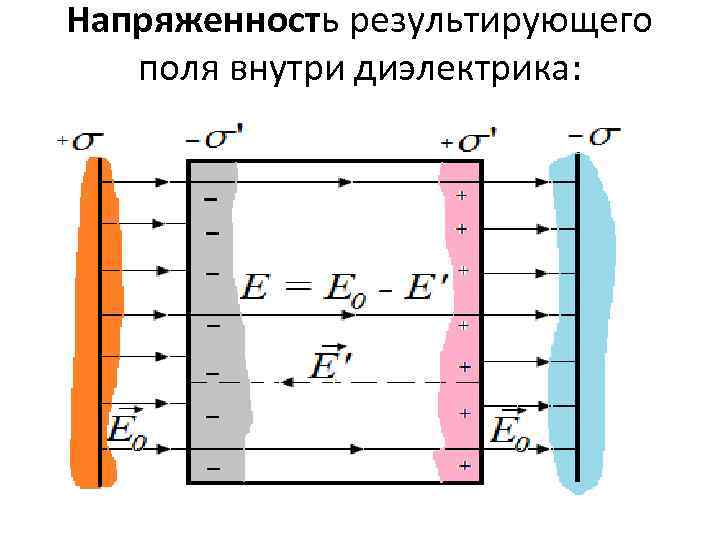 Напряженность результирующего поля внутри диэлектрика:
Напряженность результирующего поля внутри диэлектрика:
 ( C ) ( F ) ( G ) • или N — диэлектрическая восприимчивость вещества, характеризующая свойства диэлектрика
( C ) ( F ) ( G ) • или N — диэлектрическая восприимчивость вещества, характеризующая свойства диэлектрика
 Диэлектрики, молекулы которых имеют ионное строение Диэлектриками называются вещества, Диэлектрики с жёстко которые при обычных связанными молекулами условиях практически не проводят электрический Диэлектрики молекулы, которых ток. не имеют полюсы ( B )( D ) ( E )
Диэлектрики, молекулы которых имеют ионное строение Диэлектриками называются вещества, Диэлектрики с жёстко которые при обычных связанными молекулами условиях практически не проводят электрический Диэлектрики молекулы, которых ток. не имеют полюсы ( B )( D ) ( E )
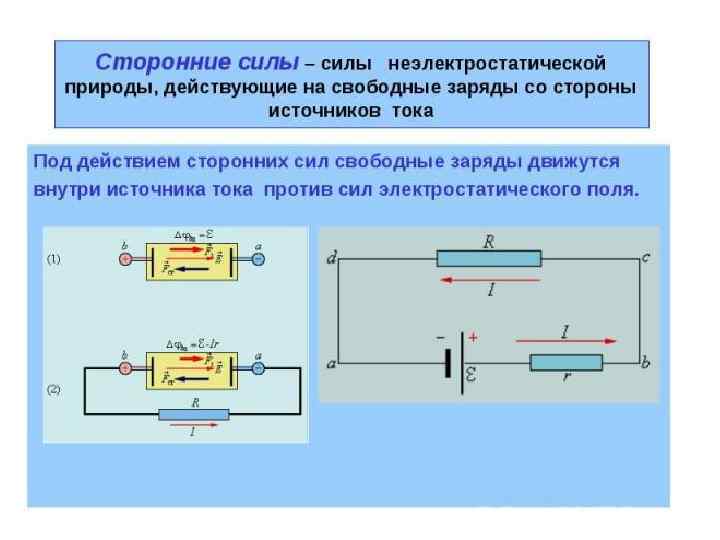
 Деформационная (электронная) поляризация наблюдается для веществ с неполярными молекулами. Ориентационная или дипольная поляризация диэлектрика с полярными молекулами, заключающаяся в ориентации (B) имеющихся дипольных моментов молекул по полю (D) Ионная поляризация диэлектриков с ионными (F) кристаллическими решетками, заключающаяся в смещении подрешетки положительных ионов вдоль поля, а отрицательных – против поля, приводящем к возникновению дипольных моментов.
Деформационная (электронная) поляризация наблюдается для веществ с неполярными молекулами. Ориентационная или дипольная поляризация диэлектрика с полярными молекулами, заключающаяся в ориентации (B) имеющихся дипольных моментов молекул по полю (D) Ионная поляризация диэлектриков с ионными (F) кристаллическими решетками, заключающаяся в смещении подрешетки положительных ионов вдоль поля, а отрицательных – против поля, приводящем к возникновению дипольных моментов.

 (B ) (G )
(B ) (G )
 ( B ) ( F )
( B ) ( F )
 ( A ) ( D ) Ёмкости цилиндрического конденсатора, состоящего из двух полых коаксиаль ных цилиндров с радиусами 1 и r 2 r
( A ) ( D ) Ёмкости цилиндрического конденсатора, состоящего из двух полых коаксиаль ных цилиндров с радиусами 1 и r 2 r
 (A ) (D ) сферический • плоский • цилиндрический
(A ) (D ) сферический • плоский • цилиндрический
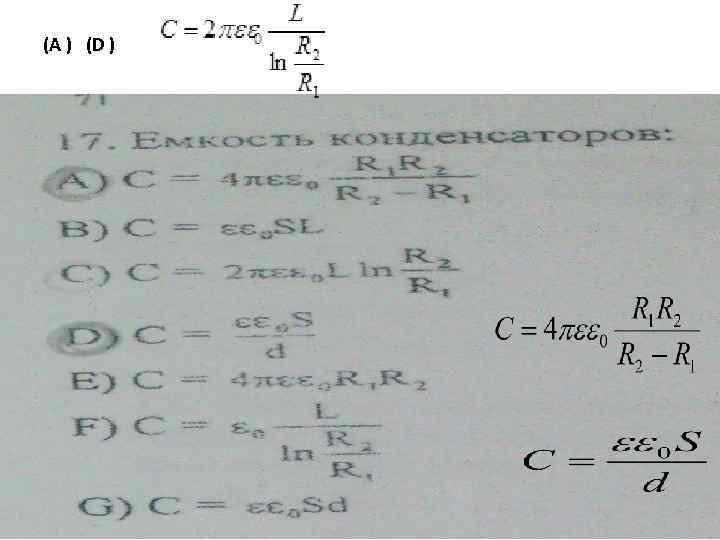 (A ) (D )
(A ) (D )
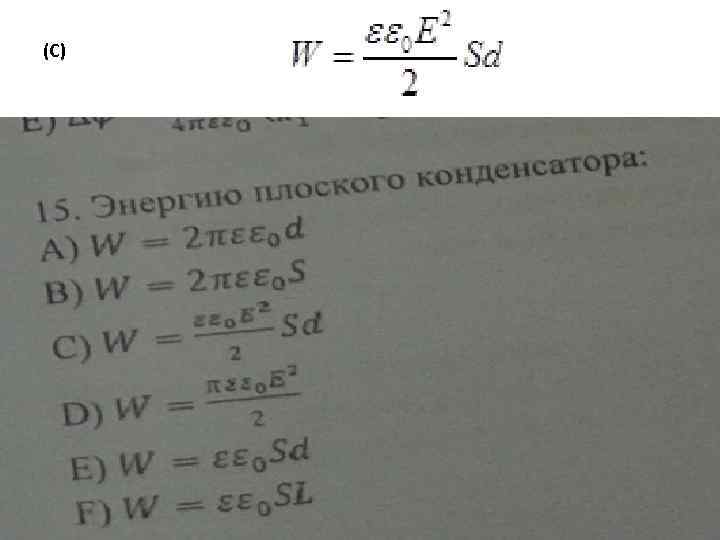 (С)
(С)
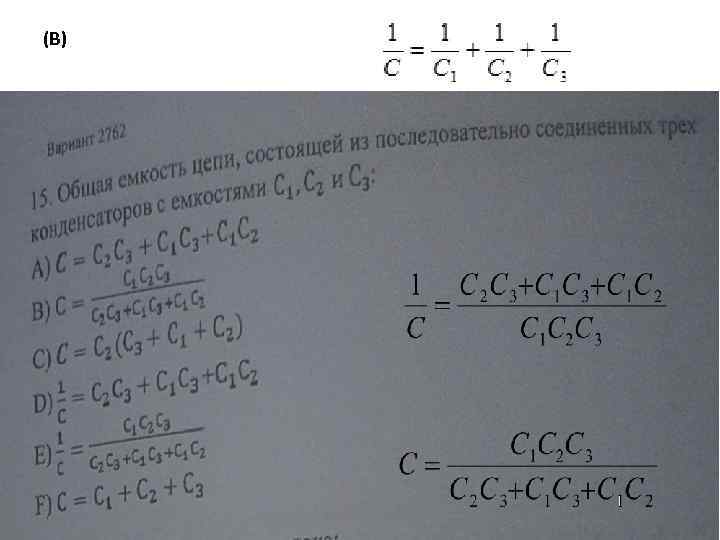 (В)
(В)
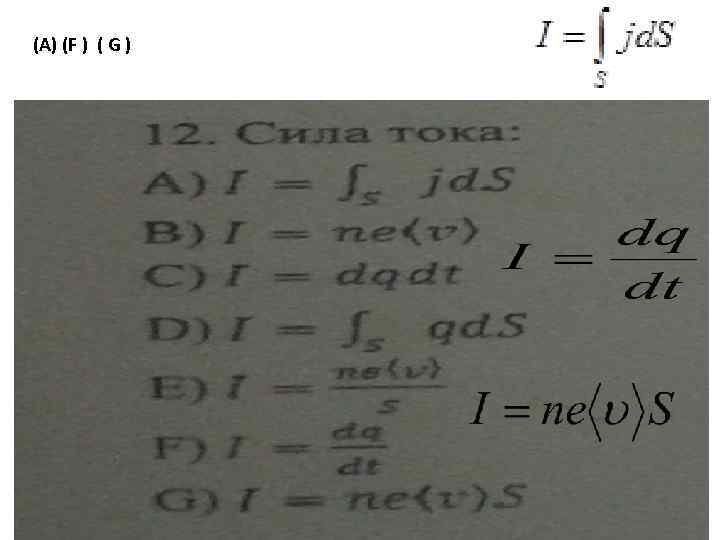 (А) (F ) ( G )
(А) (F ) ( G )
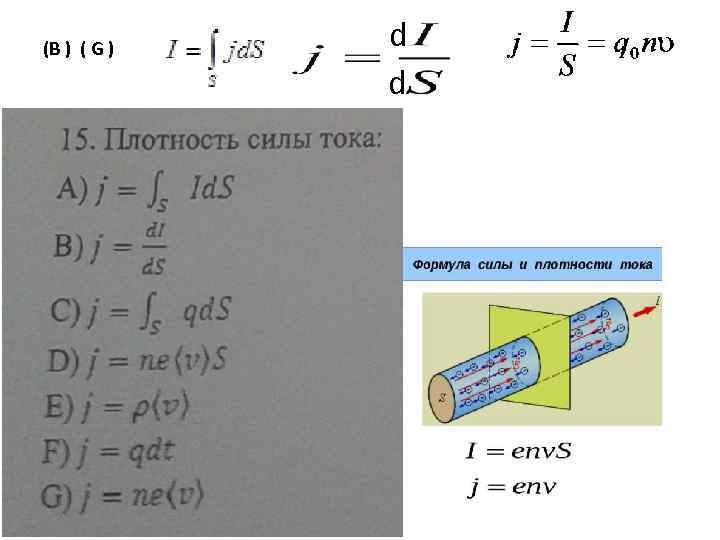 (B ) ( G ) d d
(B ) ( G ) d d
 ( E ) ( G )
( E ) ( G )
 ( D ) ( F )
( D ) ( F )
 (B )
(B )

 ( D ) ( E )
( D ) ( E )
 ( B ) ( E )
( B ) ( E )
 (F ) (G )
(F ) (G )
 ( C ) (E ) • При изменении магнитного потока в проводящем контуре возникает ЭДС индукции • Возникновение электрического тока в замкнутом проводящем контуре при изменении во времени магнитного потока, пронизывающего контур
( C ) (E ) • При изменении магнитного потока в проводящем контуре возникает ЭДС индукции • Возникновение электрического тока в замкнутом проводящем контуре при изменении во времени магнитного потока, пронизывающего контур

 • Векторное произведение обозначается символом • c ×b =a или c b =[a ].
• Векторное произведение обозначается символом • c ×b =a или c b =[a ].
 ( F ) ( C)
( F ) ( C)

 ( D ) ( E )
( D ) ( E )
 (B ) ( D )
(B ) ( D )
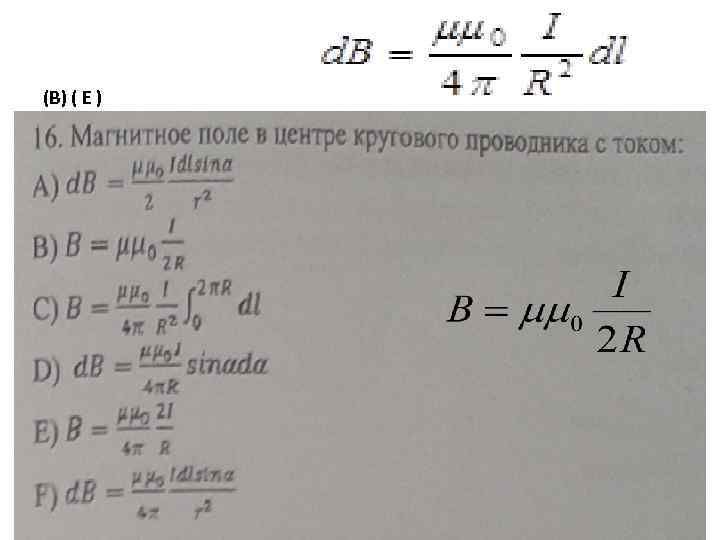 (B) ( E )
(B) ( E )
 (D ) (E ) Два определения. При изменении магнитного потока в проводящем контуре возникает ЭДС индукции Возникновение электрического тока в замкнутом проводящем контуре при изменении во времени магнитного потока, пронизывающего контур
(D ) (E ) Два определения. При изменении магнитного потока в проводящем контуре возникает ЭДС индукции Возникновение электрического тока в замкнутом проводящем контуре при изменении во времени магнитного потока, пронизывающего контур

 (A ) •
(A ) •
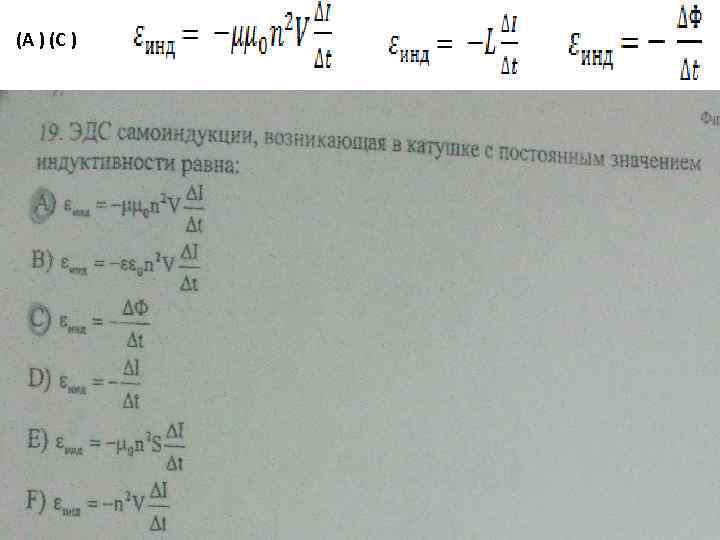 (A ) (C )
(A ) (C )
 (E ) ( F )
(E ) ( F )
 (D ) (F ) •
(D ) (F ) •

 (С ) (Е ) гиромагнитное отношением орбитальных моментов
(С ) (Е ) гиромагнитное отношением орбитальных моментов
 ( Е ) ( G )
( Е ) ( G )
 ( С ) ( D ) Точка при которой ферромагнетик теряет свои магнитные свойства При нагревании образца выше точки Кюри ферромагнетик превращается в обычный парамагнетик
( С ) ( D ) Точка при которой ферромагнетик теряет свои магнитные свойства При нагревании образца выше точки Кюри ферромагнетик превращается в обычный парамагнетик
 ( C ) ( F ) (G) Изменение магнитного потока, пронизывающего контур связано с изменением во времени электрического поля при неподвижном контуре Изменение магнитного потока, пронизывающего контур связано с изменением во времени магнитного поля при неподвижном контуре Магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле
( C ) ( F ) (G) Изменение магнитного потока, пронизывающего контур связано с изменением во времени электрического поля при неподвижном контуре Изменение магнитного потока, пронизывающего контур связано с изменением во времени магнитного поля при неподвижном контуре Магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле
 0, 09 м 9 • 10 -2 м Решение ниже
0, 09 м 9 • 10 -2 м Решение ниже

 (B ) (C) Смотри ниже
(B ) (C) Смотри ниже



 ( C ) (E ) ( F) ∆ Ф =ɛ ∆t/N
( C ) (E ) ( F) ∆ Ф =ɛ ∆t/N

 См. ниже
См. ниже
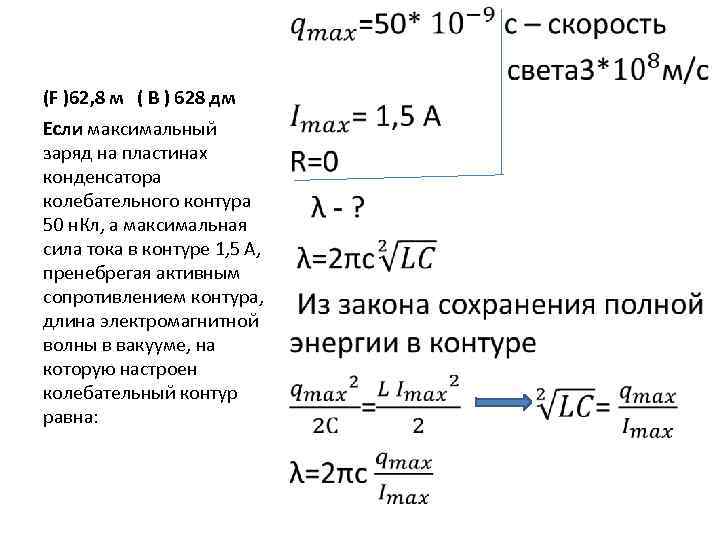 • (F )62, 8 м ( B ) 628 дм Если максимальный заряд на пластинах конденсатора колебательного контура 50 н. Кл, а максимальная сила тока в контуре 1, 5 А, пренебрегая активным сопротивлением контура, длина электромагнитной волны в вакууме, на которую настроен колебательный контур равна:
• (F )62, 8 м ( B ) 628 дм Если максимальный заряд на пластинах конденсатора колебательного контура 50 н. Кл, а максимальная сила тока в контуре 1, 5 А, пренебрегая активным сопротивлением контура, длина электромагнитной волны в вакууме, на которую настроен колебательный контур равна:
 6370 п. Кл (С) 6, 37 н. Кл 0, 00637 мк. Кл Смотреть предыдущую задачу •
6370 п. Кл (С) 6, 37 н. Кл 0, 00637 мк. Кл Смотреть предыдущую задачу •
 ( D) Cмотреть далее
( D) Cмотреть далее
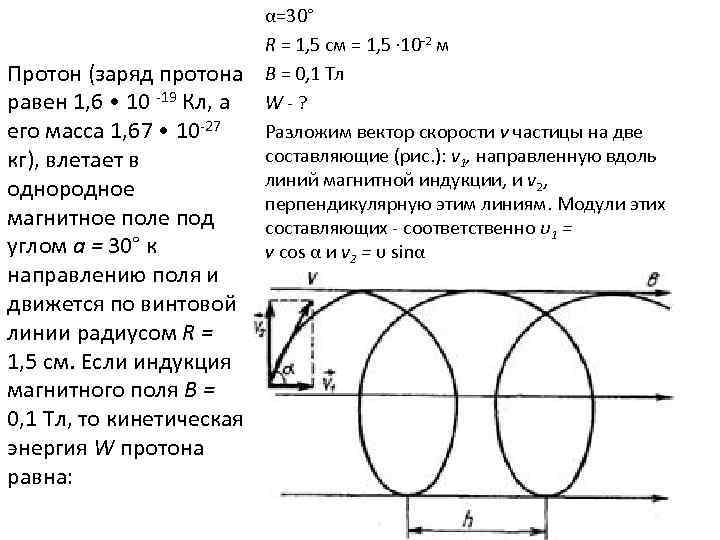 Протон (заряд протона равен 1, 6 • 10 19 Кл, а его масса 1, 67 • 10 27 кг), влетает в однородное магнитное поле под углом а = 30° к направлению поля и движется по винтовой линии радиусом R = 1, 5 см. Если индукция магнитного поля В = 0, 1 Тл, то кинетическая энергия W протона равна: α=30° R = 1, 5 см = 1, 5 · 10 2 м В = 0, 1 Тл W ? Разложим вектор скорости ν частицы на две составляющие (рис. ): v 1, направленную вдоль линий магнитной индукции, и v 2, перпендикулярную этим линиям. Модули этих составляющих соответственно υ1 = ν cos α и v 2 = υ sinα
Протон (заряд протона равен 1, 6 • 10 19 Кл, а его масса 1, 67 • 10 27 кг), влетает в однородное магнитное поле под углом а = 30° к направлению поля и движется по винтовой линии радиусом R = 1, 5 см. Если индукция магнитного поля В = 0, 1 Тл, то кинетическая энергия W протона равна: α=30° R = 1, 5 см = 1, 5 · 10 2 м В = 0, 1 Тл W ? Разложим вектор скорости ν частицы на две составляющие (рис. ): v 1, направленную вдоль линий магнитной индукции, и v 2, перпендикулярную этим линиям. Модули этих составляющих соответственно υ1 = ν cos α и v 2 = υ sinα
 •
•
 •
•
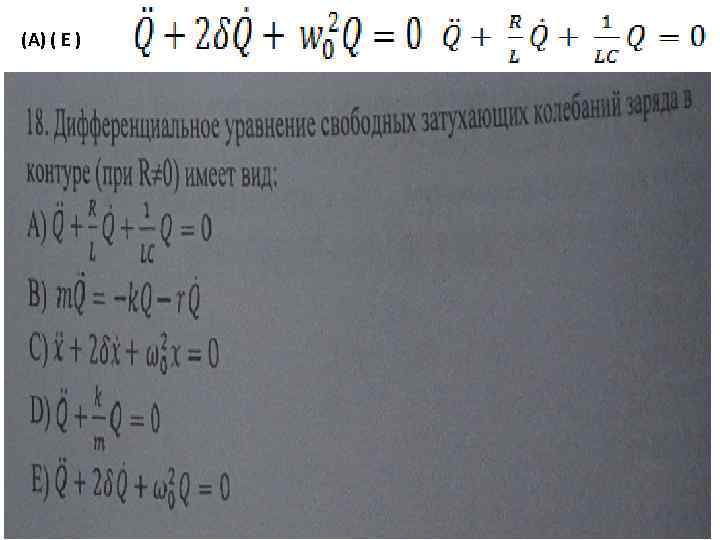 (А) ( Е )
(А) ( Е )

 (Е ) ( F) • δ коэффициент затухания
(Е ) ( F) • δ коэффициент затухания
 Дифференциальное уравнение электромагнитной волны оператор Лапласа, v — фазовая ско рость. Тогда
Дифференциальное уравнение электромагнитной волны оператор Лапласа, v — фазовая ско рость. Тогда
 ( A )
( A )

 (G )
(G )
 См. ниже
См. ниже