Voronoi Diagrams Tutorial 3 Computational Geometry

Voronoi Diagrams Tutorial 3 – Computational Geometry

Simple Voronoi diagrams n n A tessellation of the planes into cells. Each cell is the set of points closed to a point site (Euclidean metric). All edges are parts of bisectors between the sites.

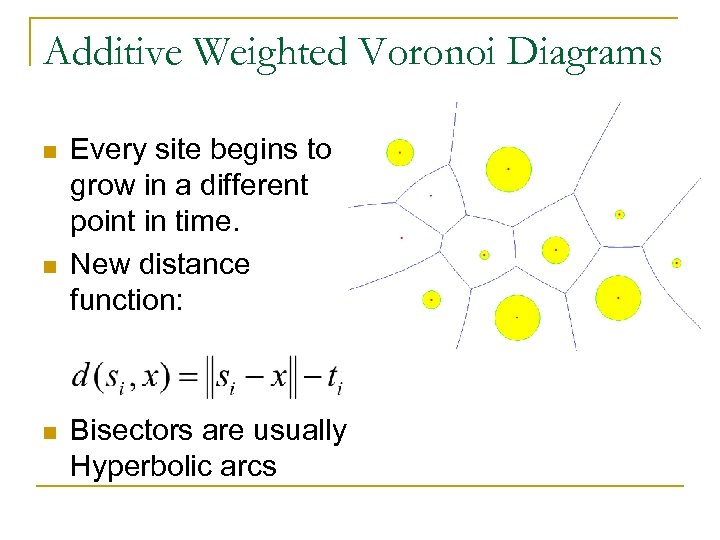Additive Weighted Voronoi Diagrams n n n Every site begins to grow in a different point in time. New distance function: Bisectors are usually Hyperbolic arcs

Multiplicatively-Weighted Diagrams n n Each site grows at different rate. Distance function: Bisectors are usually circular arcs. Regions can be surrounded.

Different Metrics - n Metric is defined as: n Also called “Manhattan Distances” because it measures distances through axis-aligned streets.

Centroidal Voronoi Diagrams n n n Each site is also the center-of-mass of each cell. Points are distributed evenly. Uses: data compression, quantization, optimal mesh generation, etc.

CVD Computation: Lloyd’s Algorithm n n Given a set of sites : Compute VD. While (tolerance value not reached): q Move sites to center of respective cells. q Recompute VD. Tolerance value is a function of distance from the sites to the respective centers of cells.

Lloyd’s Algorithm – cont’d n n Converges to a centroidal Voronoi diagram – slowly. Simple to apply. Because of slow convergence, the algorithm stops at a tolerance value. Computing of centroid of a polygon (CCW order of the vertices :

Higher Dimensions Voronoi Diagrams n n n Cells are convex polytopes. Bisectors are (d-1)halfplanes. Complexity:

Bibliography: n n n Voronoi Applet: http: //www. pi 6. fernunihagen. de/Geom. Lab/voroadd/ Reitsma, Stanislav Trubin, Saurabh Sethia, "Information Space Regionalization Using Adaptive Multiplicatively Weighted Voronoi Diagrams, " iv, pp. 290294, Eighth International Conference on Information Visualisation (IV'04), 2004 Wikipedia – Voronoi Diagrams.