Вопросы по теме • Устойчивость

Вопросы по теме • Устойчивость САУ. Определение устойчивости ЛНС САУ 1 -го порядка по дифференциальному уравнению. Определение устойчивости ЛНС САУ n-го порядка по дифференциальному уравнению. Качественный критерий устойчивости Ляпунова А. М. Определение устойчивости системы по характеристическим уравнениям. Алгебраический критерий устойчивости (Рауса-Гурвица). Амплитудно-фазовый критерий Найквиста. Определение устойчивости системы по логарифмическим характеристикам. Частотный критерий Михайлова А. В.

Устойчивость САУ. • Понятие устойчивости связано со способностью системы возвращаться в исходное состояние равновесия после исчезновения внешних возмущающих сил, прилагаемых к системе. Если при отсутствии входного сигнала x(t) выходной сигнал не меняется, то такие состояния называются состоянием равновесия. В ЛН САУ состояние устойчивости можно оценить тремя способами: • 1. Путем анализа корней дифура САУ в «свободном» состоянии. • 2. Путем анализа корней характеристического уравнения САУ. • 3. С помощью различных критериев устойчивости

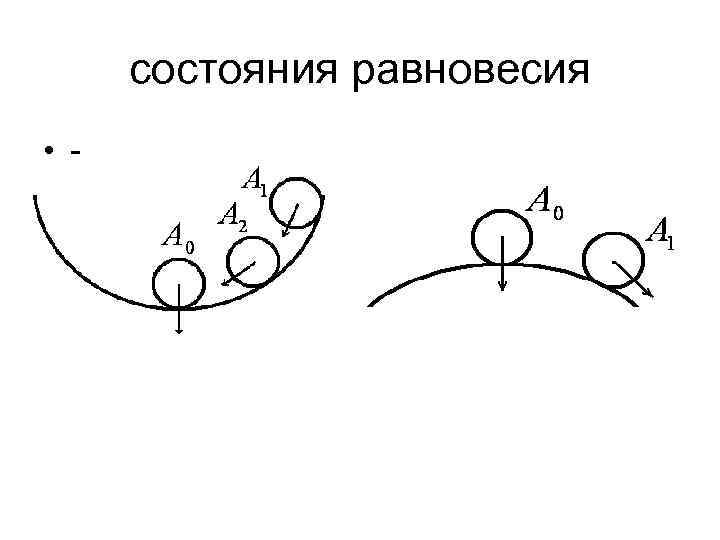
состояния равновесия • -

Определение устойчивости ЛНС САУ 1 -го порядка по дифференциальному уравнению (1 -ый способ): • -

Определение устойчивости ЛНС САУ 1 -го порядка по дифференциальному уравнению (1 -ый способ): t • -

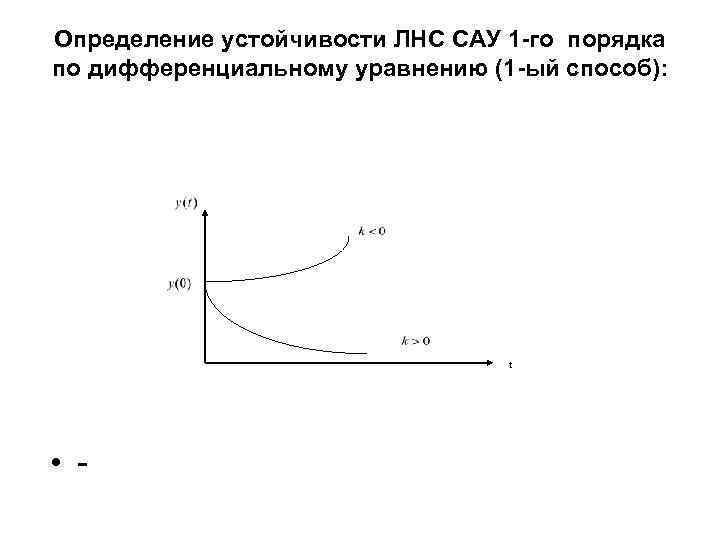
Определение устойчивости ЛНС САУ n-го порядка по дифференциальному уравнению (1 -ый способ): • -

Свободное состояние САУ • -

Качественный критерий устойчивости Ляпунова А. М. • Определение устойчивости методом Ляпунова А. М. заключается в следующем: • Для определения устойчиво ли состояние равновесия необходимо к системе приложить возмущение и рассмотреть движение системы после снятия возмущения. Устойчивая ЛН САУ стремится к исходному состоянию. Неустойчивая САУ– удаляется от состояния равновесия. Реальная неустойчивая система со временем переходит в нелинейный режим и возникают автоколебания

Определение устойчивости системы по характеристическим уравнениям • -Дифференциальное уравнение, описывающее свободные колебания в системе, имеет вид

Определение устойчивости системы по характеристическим уравнениям

Определение устойчивости системы по характеристическим уравнениям • Характеристическое уравнение:

Определение устойчивости системы по характеристическим уравнениям • Если хотя-бы один корень имеет положительную действительную часть, то САУ будет неустойчивой • На практике ДУ не решают, а используют специальные критерии. Эти критерии исходят из следующего: необходимым и достаточным условием устойчивости ЛНС САУ является отрицательность действительных частей всех корней характеристического уравнения. Существуют разные формы критериев, но они математически эквивалентны, т. к. определяются только этими условиями. Наиболее распространены: • - Критерий Рауса-Гурвица (алгебраический), • - Критерий Найквиста (амплитудно-фазовый). • - Критерий Михайлова А. В.

Алгебраический критерий (Рауса-Гурвица).

Алгебраический критерий (Рауса-Гурвица). • - n=3 n=4

Алгебраический критерий (Рауса-Гурвица). • Для САУ 1 -го 2 -го порядка система будет устойчивой, если выполняется только необходимое условие. • Достаточные условия в общем случае являются определителями матрицы Гурвица, показанной ниже.

матрица Гурвица, • - М=

Алгебраический критерий (Рауса-Гурвица). • .

Алгебраический критерий (Рауса-Гурвица). • Определители Гурвица получают из матрицы Гурвица отчеркиванием строк и столбцов, на пересечении которых стоит .

Для САУ третьего порядка ( т. е. n=3 и для этой САУ начинают действовать достаточные условия ) определитель Гурвица равен: • -

Алгебраический критерий (Рауса-Гурвица). • Он получен из матрицы

Для систем с порядком дифференциального уравнения, описывающего САУ, равным: n=4 и n=5 соответственно: • - Определители Гурвица для устойчивой САУ должны быть больше нуля.

Алгебраический критерий (Рауса-Гурвица). • Определитель вычисляется обычным способом. Он равен сумме произведений элементов какой-либо строки ( или какого-либо столбца ) на их алгебраические дополнения. Алгебраическим дополнением элемента называется его минор, взятый со знаком ( + ) или (- ). • Причем, если сумма номеров столбца и строки, на пересечении которых стоит элемент, есть число четное, то минор берется со знаком ( + ) , если нечетное – то ( - ) • Минор элемента –это определитель, полученный из данного определителя вычеркиванием той строки и того столбца, на пересечении которых стоит элемент.

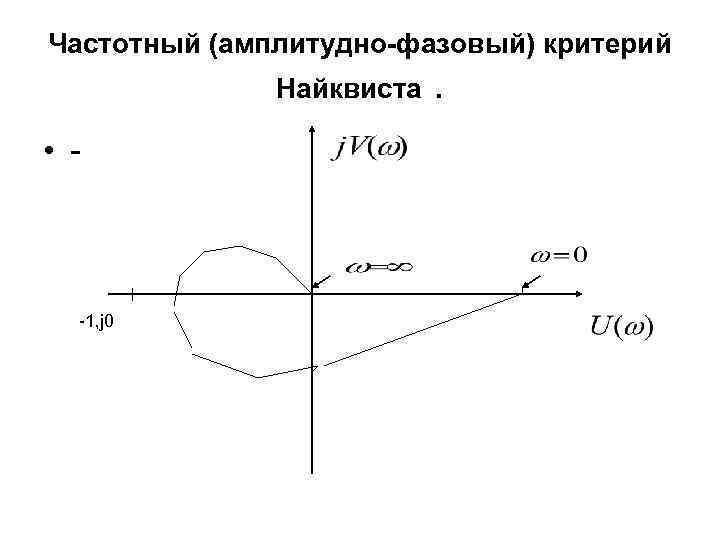
Частотный (амплитудно-фазовый) критерий Найквиста • Позволяет оценить устойчивость замкнутой САУ по АФХ и ЛАЧХ разомкнутой системы. • Если точки с координатами (-1; j 0) АФХ не охватывается контуром, образованным АФХ, то замкнутая САУ устойчива.

Частотный (амплитудно-фазовый) критерий Найквиста . • - -1, j 0

Частотный (амплитудно-фазовый) критерий Найквиста • . В случае, если САУ имеет интегрирующие звенья и АФХ при уходит в бесконечность, то для образования замкнутого контура нужно провести дугу окружности большого радиуса.

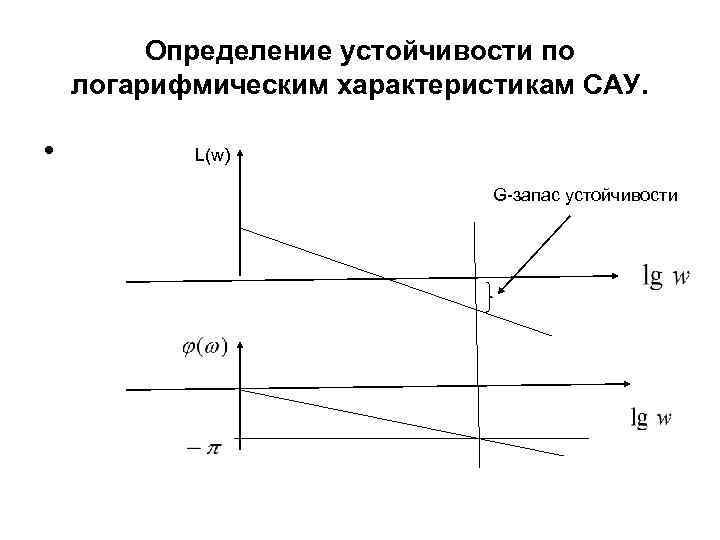
Определение устойчивости по логарифмическим характеристикам САУ. • Замкнутая система устойчива, если на частоте w ( см. ниже на рисунке 1), соответствующей φ(w) = -π, ордината ЛАЧХ имеет отрицательный знак, т. е. 20 lg | k(w) | <0, • где G- запас устойчивости

Определение устойчивости по логарифмическим характеристикам САУ. • L(w) G-запас устойчивости

Частотный критерий Михайлова А. В. • .

Частотный критерий Михайлова А. В. • Если в этом уравнении выполнить замену параметра на jw, то получим вектор

Частотный критерий Михайлова А. В. • Кривая, описываемая на комплексной плоскости концом вектора N(jw) при изменении w от нуля до бесконечности, называется годографом Михайлова. • Для того чтобы САУ была устойчивой необходимо и достаточно, чтобы годограф Михайлова начинался на положительной части действительной оси и проходил последовательно в положительном направлении, т. е против часовой стрелки, не попадая в начало координат, n квадрантов комплексной плоскости, где n – порядок характеристического уравнения.

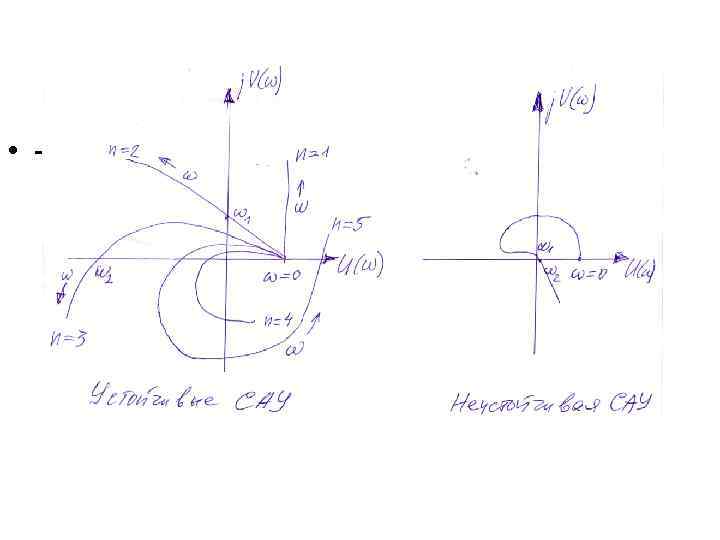
Частотный критерий Михайлова А. В. • Математически это записывается следующим образом: • при • • Графически это показано ниже на рисунках.

• -