 Вопросы по лекции № 1 1. Что такое плазма 2. Концентрация (плотность) 3. Степень ионизации (два определения) 4. Ленгмюровская частота 5. Электронный дебаевский радиус 6. Квазинейтральность плазмы 7. Температура плазмы
Вопросы по лекции № 1 1. Что такое плазма 2. Концентрация (плотность) 3. Степень ионизации (два определения) 4. Ленгмюровская частота 5. Электронный дебаевский радиус 6. Квазинейтральность плазмы 7. Температура плазмы
 Лекция № 2 Электромагнитные волны Электронно-плазменные (ленгмюровские волны) Ионно-звуковые и ионно-плазменные волны Распространение космических лучей в межзвёздной среде Рассеяние быстрых частиц в слаботурбулентной плазме Диффузионное приближение
Лекция № 2 Электромагнитные волны Электронно-плазменные (ленгмюровские волны) Ионно-звуковые и ионно-плазменные волны Распространение космических лучей в межзвёздной среде Рассеяние быстрых частиц в слаботурбулентной плазме Диффузионное приближение
 Колебания и волны в плазме Коллективность плазменных процессов позволяет легко возбуждать в плазме колебания и волны различных типов. Колебания характеризуют частотой ω , а волны, кроме частоты, длиной волны λ, волновым вектором k, а также рядом др. параметров. Между частотой и волновым вектором k (или волновым числом k = | k |=2π/ λ) существует связь, называемая дисперсионным соотношением: ω= vф k
Колебания и волны в плазме Коллективность плазменных процессов позволяет легко возбуждать в плазме колебания и волны различных типов. Колебания характеризуют частотой ω , а волны, кроме частоты, длиной волны λ, волновым вектором k, а также рядом др. параметров. Между частотой и волновым вектором k (или волновым числом k = | k |=2π/ λ) существует связь, называемая дисперсионным соотношением: ω= vф k
 Колебания и волны в плазме Т. к. фазовая скорость волны, т. е. скорость строго монохроматической волны, vф = ω/ k, дисперсионное соотношение даёт также зависимость vф, от ω или λ. В обычном, не ионизованном, газе могут распространяться волны различных типов, их дисперсионные соотношения очень просты. Например, для звуковых волн малой амплитуды ω= vs k, где vs - скорость звука. Здесь vф = vs, т. е. скорость не зависит от частоты или длины волны.
Колебания и волны в плазме Т. к. фазовая скорость волны, т. е. скорость строго монохроматической волны, vф = ω/ k, дисперсионное соотношение даёт также зависимость vф, от ω или λ. В обычном, не ионизованном, газе могут распространяться волны различных типов, их дисперсионные соотношения очень просты. Например, для звуковых волн малой амплитуды ω= vs k, где vs - скорость звука. Здесь vф = vs, т. е. скорость не зависит от частоты или длины волны.
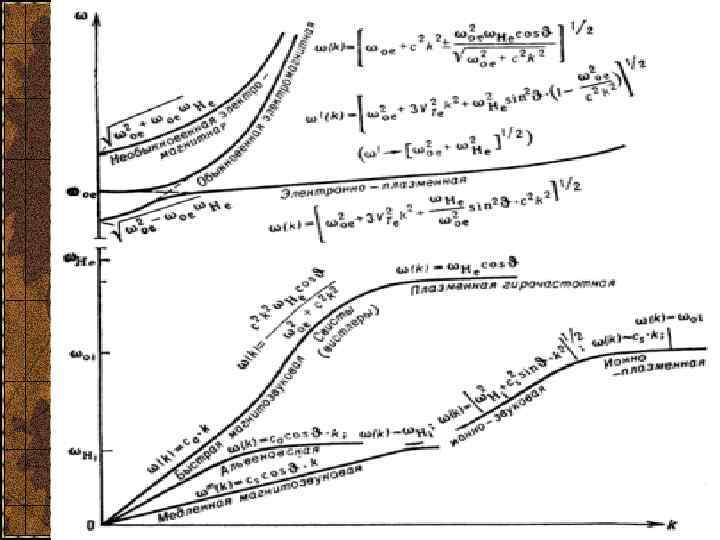
 Колебания и волны в плазме В плазме значительно больше различных типов волн, и их дисперсионные соотношения много сложнее. На следующем рисунке схематически, без соблюдения масштаба, нанесены дисперсионные соотношения бесстолкновительной плазмы низкого давления. Далее рассмотрим основных видов плазменных волн и их св-ва.
Колебания и волны в плазме В плазме значительно больше различных типов волн, и их дисперсионные соотношения много сложнее. На следующем рисунке схематически, без соблюдения масштаба, нанесены дисперсионные соотношения бесстолкновительной плазмы низкого давления. Далее рассмотрим основных видов плазменных волн и их св-ва.

 Электромагнитные волны в плазме без магнитного поля В плазме без магн. поля (H 0=0) эл. -магн. волны являются поперечными. Дисперсионное соотношение для эл. -магн. волн в плазме: (3) и где ленгмюровская частота (4)
Электромагнитные волны в плазме без магнитного поля В плазме без магн. поля (H 0=0) эл. -магн. волны являются поперечными. Дисперсионное соотношение для эл. -магн. волн в плазме: (3) и где ленгмюровская частота (4)
 Электромагнитные волны в плазме без магнитного поля Из (4) следует, что фазовая скорость радиоволн в плазме vф > c и что эл. -магн. волны с частотой, меньшей ленгмюровской (ω<<ω 0 е), в плазме распространяться не могут. С другой стороны, эл. -магн. волны с большей частотой, распространяясь в сторону увеличения электронной концентрации, испытывают полное внутреннее отражение.
Электромагнитные волны в плазме без магнитного поля Из (4) следует, что фазовая скорость радиоволн в плазме vф > c и что эл. -магн. волны с частотой, меньшей ленгмюровской (ω<<ω 0 е), в плазме распространяться не могут. С другой стороны, эл. -магн. волны с большей частотой, распространяясь в сторону увеличения электронной концентрации, испытывают полное внутреннее отражение.
 Электромагнитные волны в плазме без магнитного поля Эти особенности важны при исследовании распространения радиоволн в солнечной короне, межзвёздном газе и ионосфере. В результате непрозрачность ионосферы для этих волн ограничивает с длинноволновой стороны "радиоастрономическое окно" прозрачности земной атмосферы и, с др. стороны, обеспечивает распространение радиоволн вдоль земной поверхности.
Электромагнитные волны в плазме без магнитного поля Эти особенности важны при исследовании распространения радиоволн в солнечной короне, межзвёздном газе и ионосфере. В результате непрозрачность ионосферы для этих волн ограничивает с длинноволновой стороны "радиоастрономическое окно" прозрачности земной атмосферы и, с др. стороны, обеспечивает распространение радиоволн вдоль земной поверхности.
 Электромагнитные волны в плазме с внешним магнитным полем Распространение радиоволн в П. , находящейся во внешнем магнитном поле (H 0>0), обладает рядом особенностей. Гирочастота – ωНе. Наиболее прост и чаще всего встречается случай "квазипродольного распространения", когда и угол между волновым вектором волны k и направлением внешнего магн. поля H 0 не слишком близок к π/2 , т. е. волна распространяется не точно поперёк поля.
Электромагнитные волны в плазме с внешним магнитным полем Распространение радиоволн в П. , находящейся во внешнем магнитном поле (H 0>0), обладает рядом особенностей. Гирочастота – ωНе. Наиболее прост и чаще всего встречается случай "квазипродольного распространения", когда и угол между волновым вектором волны k и направлением внешнего магн. поля H 0 не слишком близок к π/2 , т. е. волна распространяется не точно поперёк поля.
 Электромагнитные волны в плазме с внешним магнитным полем Если в плазме без магнитного поля эл. магн. волна остаётся всё время линейно поляризованной, т. е. направление её электрического вектора не меняется при распространении, то в плазме с магнитным полем эл. -магн. волны оказываются поляризованными по кругу или эллиптически поляризованными в более общем случае.
Электромагнитные волны в плазме с внешним магнитным полем Если в плазме без магнитного поля эл. магн. волна остаётся всё время линейно поляризованной, т. е. направление её электрического вектора не меняется при распространении, то в плазме с магнитным полем эл. -магн. волны оказываются поляризованными по кругу или эллиптически поляризованными в более общем случае.
 Электромагнитные волны в плазме с внешним магнитным полем Круговая поляризация в случае квазипродольного распространения объясняется возникновением в П. двух волн обыкновенной и необыкновенной. Электрич. вектор необыкновенной волны вращается по кругу в ту же сторону, что и электроны, Электрич. вектор обыкновенной волны - в противоположную сторону.
Электромагнитные волны в плазме с внешним магнитным полем Круговая поляризация в случае квазипродольного распространения объясняется возникновением в П. двух волн обыкновенной и необыкновенной. Электрич. вектор необыкновенной волны вращается по кругу в ту же сторону, что и электроны, Электрич. вектор обыкновенной волны - в противоположную сторону.
 Электромагнитные волны в плазме с внешним магнитным полем Обыкновенная и необыкновенная волны распространяются в П. с разной скоростью и с разными показателями поглощения, последний у необыкновенной волны, как правило, больше. Это, в частности, приводит к тому, что у ряда космических источников наблюдается только излучение, поляризованное по кругу (чаще всего обыкновенная волна). Исследование поляризации эл. -магн. волн, распространяющихся в космич. П. , служит одним из важнейших источников сведений о космических магнитных полях.
Электромагнитные волны в плазме с внешним магнитным полем Обыкновенная и необыкновенная волны распространяются в П. с разной скоростью и с разными показателями поглощения, последний у необыкновенной волны, как правило, больше. Это, в частности, приводит к тому, что у ряда космических источников наблюдается только излучение, поляризованное по кругу (чаще всего обыкновенная волна). Исследование поляризации эл. -магн. волн, распространяющихся в космич. П. , служит одним из важнейших источников сведений о космических магнитных полях.
 Электронно-плазменные (ленгмюровские) волны При смещении электронов плазмы. относительно ионов возникает электростатическая сила, стремящаяся вернуть их в положение равновесия. Коллективность плазменных процессов приведёт к тому, что в колебаниях сразу примет участие много электронов. Если температура плазмы мала, то возникают только т. н. электростатические колебания на частоте ω0 е.
Электронно-плазменные (ленгмюровские) волны При смещении электронов плазмы. относительно ионов возникает электростатическая сила, стремящаяся вернуть их в положение равновесия. Коллективность плазменных процессов приведёт к тому, что в колебаниях сразу примет участие много электронов. Если температура плазмы мала, то возникают только т. н. электростатические колебания на частоте ω0 е.
 Электронно-плазменные (ленгмюровские) волны При увеличении температуры и усилении теплового движения электронов появляются ленгмюровские волны. Эти волны, подобно звуковым, продольные. Ионы в их распространении не участвуют, т. к. обладают большой массой и не могут колебаться с высокой частотой, с какой колеблются электроны.
Электронно-плазменные (ленгмюровские) волны При увеличении температуры и усилении теплового движения электронов появляются ленгмюровские волны. Эти волны, подобно звуковым, продольные. Ионы в их распространении не участвуют, т. к. обладают большой массой и не могут колебаться с высокой частотой, с какой колеблются электроны.
 Электронно-плазменные (ленгмюровские) волны Движение электронов происходит в этом случае под действием двух факторов: перепада их давления и электрического поля. В отличие от эл. -магн. волн, здесь вектор электрического поля направлен вдоль вектора k (продольные электрич. волны). Магнитное поле при ω 0 е >>ωНе не влияет существенно на св-ва ленгмюровских волн. ωНе - гиромагнитная частота
Электронно-плазменные (ленгмюровские) волны Движение электронов происходит в этом случае под действием двух факторов: перепада их давления и электрического поля. В отличие от эл. -магн. волн, здесь вектор электрического поля направлен вдоль вектора k (продольные электрич. волны). Магнитное поле при ω 0 е >>ωНе не влияет существенно на св-ва ленгмюровских волн. ωНе - гиромагнитная частота
 Электронно-плазменные (ленгмюровские) волны Фазовая скорость плазменных волн: где νТе - тепловая скорость электронов. vф может быть даже больше скорости света (если ω = ω 0 е ). Если ω не слишком близка к ω0 е , то фазовая скорость плазменной волны может быть много меньше скорости света. При этом длина волны близка к величине дебаевского радиуса.
Электронно-плазменные (ленгмюровские) волны Фазовая скорость плазменных волн: где νТе - тепловая скорость электронов. vф может быть даже больше скорости света (если ω = ω 0 е ). Если ω не слишком близка к ω0 е , то фазовая скорость плазменной волны может быть много меньше скорости света. При этом длина волны близка к величине дебаевского радиуса.
 Электронно-плазменные (ленгмюровские) волны Однако такие волны очень быстро затухают, т. к. в плазме есть много электронов, попадающих в резонанс с подобными волнами и забирающих у них энергию (затухание Ландау - бесстолкновительное затухание колебаний и волн в плазме ). Поэтому могут существовать только волны ω -ω 0 е <<ω0 е. В магнитном поле бесстолкновительное затухание волн связано не только с затуханием Ландау, но и с циклотронным затуханием. Физический механизм, лежащий в основе циклотронного затухания (резонанс), аналогичен механизму затухания Ландау.
Электронно-плазменные (ленгмюровские) волны Однако такие волны очень быстро затухают, т. к. в плазме есть много электронов, попадающих в резонанс с подобными волнами и забирающих у них энергию (затухание Ландау - бесстолкновительное затухание колебаний и волн в плазме ). Поэтому могут существовать только волны ω -ω 0 е <<ω0 е. В магнитном поле бесстолкновительное затухание волн связано не только с затуханием Ландау, но и с циклотронным затуханием. Физический механизм, лежащий в основе циклотронного затухания (резонанс), аналогичен механизму затухания Ландау.
 Электронно-плазменные (ленгмюровские) волны В П. всегда есть ленгмюровские волны (плазменные флуктуации), обусловленные тепловым движением частиц. Такие флуктуации имеют плотность энергии порядка k. Te/ r. De 3, и длина волны их не слишком сильно отличается от дебаевского радиуса r. De. Если в силу тех или иных причин в П. возбуждены ленгмюровские волны с длиной волны, много большей r. De , и плотностью энергии, много большей k. Te/ r. De 3, то П. становится турбулентной. Плазменная турбулентность должна поддерживаться каким-либо источником.
Электронно-плазменные (ленгмюровские) волны В П. всегда есть ленгмюровские волны (плазменные флуктуации), обусловленные тепловым движением частиц. Такие флуктуации имеют плотность энергии порядка k. Te/ r. De 3, и длина волны их не слишком сильно отличается от дебаевского радиуса r. De. Если в силу тех или иных причин в П. возбуждены ленгмюровские волны с длиной волны, много большей r. De , и плотностью энергии, много большей k. Te/ r. De 3, то П. становится турбулентной. Плазменная турбулентность должна поддерживаться каким-либо источником.
 Ионно-звуковые и ионноплазменные волны В условиях, когда температура электронов по крайней мере в 5 -10 раз больше температуры ионов, электроны распределяются в пространстве более однородно. На фоне этого равномерно распределённого отрицательного заряда могут распространяться ионно-плазменные волны с частотой, близкой к где mi - масса иона. По своим характеристикам эти продольные волны похожи на ленгмюровские, но здесь колеблются не электроны, а ионы.
Ионно-звуковые и ионноплазменные волны В условиях, когда температура электронов по крайней мере в 5 -10 раз больше температуры ионов, электроны распределяются в пространстве более однородно. На фоне этого равномерно распределённого отрицательного заряда могут распространяться ионно-плазменные волны с частотой, близкой к где mi - масса иона. По своим характеристикам эти продольные волны похожи на ленгмюровские, но здесь колеблются не электроны, а ионы.
 Ионно-звуковые и ионноплазменные волны Кроме них возможны др. продольные волны с ещё меньшими частотами, они называются ионно-звуковыми и распространяются со скоростью звука. Если электронная и ионная темп-ры почти одинаковы (изотермич. П. ), то ионные (плазменные и звуковые) волны быстро затухают, их энергия нагревает ионы. В космич. условиях ионно -плазменные волны могут возникать внутри фронтов ударных волн, где ионная температура сильно отличается от электронной.
Ионно-звуковые и ионноплазменные волны Кроме них возможны др. продольные волны с ещё меньшими частотами, они называются ионно-звуковыми и распространяются со скоростью звука. Если электронная и ионная темп-ры почти одинаковы (изотермич. П. ), то ионные (плазменные и звуковые) волны быстро затухают, их энергия нагревает ионы. В космич. условиях ионно -плазменные волны могут возникать внутри фронтов ударных волн, где ионная температура сильно отличается от электронной.
 Низкочастотные волны в плазме с магнитным полем В отсутствие магн. поля есть только один тип ионно-звуковая. При наличии магн. поля появляются три ветви колебаний Их характеристики заметно меняются в зависимости от частоты и угла между волновым вектором и полем. На частотах, меньших ионной гирочастоты это будет альвеновская и две магнитозвуковые (быстрая и медленная) волны.
Низкочастотные волны в плазме с магнитным полем В отсутствие магн. поля есть только один тип ионно-звуковая. При наличии магн. поля появляются три ветви колебаний Их характеристики заметно меняются в зависимости от частоты и угла между волновым вектором и полем. На частотах, меньших ионной гирочастоты это будет альвеновская и две магнитозвуковые (быстрая и медленная) волны.
 Низкочастотные волны в плазме с магнитным полем Их скорости распространения равны альвеновской скорости и комбинациям альвеновской скорости и скорости звука. При большей частоте одна из этих волн, соответствующая необыкновенной волне, переходит в т. н. свисты или вистлеры. Свисты обладают св-вом распространяться в П. вдоль магн. силовых линий. Такие волны наблюдаются в земной ионосфере и магнитосфере. Поскольку их частота сравнительно мала, они могут трансформироваться в звук той же частоты. По характеру этого звука их и наз. свистами.
Низкочастотные волны в плазме с магнитным полем Их скорости распространения равны альвеновской скорости и комбинациям альвеновской скорости и скорости звука. При большей частоте одна из этих волн, соответствующая необыкновенной волне, переходит в т. н. свисты или вистлеры. Свисты обладают св-вом распространяться в П. вдоль магн. силовых линий. Такие волны наблюдаются в земной ионосфере и магнитосфере. Поскольку их частота сравнительно мала, они могут трансформироваться в звук той же частоты. По характеру этого звука их и наз. свистами.
 Низкочастотные волны в плазме с магнитным полем. Обыкновенная (быстрая) магнитозвуковая волна, так же как и все другие - медленная и альвеновская, обрывается на частоте ω Нi , на которой она сильно поглощается. Рассмотренные выше волны в П. могут переходить одна в другую. Этот процесс называется конверсией. Для астрофизики особенно важен переход плазменных волн в электромагнитные.
Низкочастотные волны в плазме с магнитным полем. Обыкновенная (быстрая) магнитозвуковая волна, так же как и все другие - медленная и альвеновская, обрывается на частоте ω Нi , на которой она сильно поглощается. Рассмотренные выше волны в П. могут переходить одна в другую. Этот процесс называется конверсией. Для астрофизики особенно важен переход плазменных волн в электромагнитные.
 Низкочастотные волны в плазме. с магнитным полем. Например, плазменная волна, рассеиваясь на флуктуации электронной плотности (к-рая может быть создана движением иона или обусловлена др. плазменной волной), превращается в эл. -магн. волну с той же частотой (рэлеевское рассеяние) или удвоенной частотой (комбинац. рассеяние на плазменных волнах), или, наконец, с много большей частотой, если рассеяние происходит на релятивистском электроне.
Низкочастотные волны в плазме. с магнитным полем. Например, плазменная волна, рассеиваясь на флуктуации электронной плотности (к-рая может быть создана движением иона или обусловлена др. плазменной волной), превращается в эл. -магн. волну с той же частотой (рэлеевское рассеяние) или удвоенной частотой (комбинац. рассеяние на плазменных волнах), или, наконец, с много большей частотой, если рассеяние происходит на релятивистском электроне.
 Распространение космических лучей в межзвёздной среде Характер распространения быстрых заряженных частиц в межзвездной среде определяется, главным образом, их взаимодействием с магнитными и электрическими полями, присутствующими в космической плазме. Эффективное удержание и «перемешивание» космических лучей в Галактике, их диффузия могут в принципе обеспечиваться:
Распространение космических лучей в межзвёздной среде Характер распространения быстрых заряженных частиц в межзвездной среде определяется, главным образом, их взаимодействием с магнитными и электрическими полями, присутствующими в космической плазме. Эффективное удержание и «перемешивание» космических лучей в Галактике, их диффузия могут в принципе обеспечиваться:
 Распространение космических лучей в межзвёздной среде 1) за счет стохастической структуры галактического магнитного поля и его крупномасштабных неоднородностей; 2) в результате рассеяния частиц мелкомасштабной турбулентностью;
Распространение космических лучей в межзвёздной среде 1) за счет стохастической структуры галактического магнитного поля и его крупномасштабных неоднородностей; 2) в результате рассеяния частиц мелкомасштабной турбулентностью;
 Распространение космических лучей в межзвёздной среде 3) в силу неустойчивости анизотропных распределений релятивистских частиц в межзвездной плазме; 4) вследствие неустойчивости «галактического диска» , представляющего собой систему, включающую межзвездный газ, магнитное поле и космические лучи и удерживаемую в равновесии в конечном счете за счет гравитационного поля звезд.
Распространение космических лучей в межзвёздной среде 3) в силу неустойчивости анизотропных распределений релятивистских частиц в межзвездной плазме; 4) вследствие неустойчивости «галактического диска» , представляющего собой систему, включающую межзвездный газ, магнитное поле и космические лучи и удерживаемую в равновесии в конечном счете за счет гравитационного поля звезд.
 Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Одно из основных свойств плазмы состоит в том, что в ней легко возбуждаются различные типы колебаний и волн. Турбулентные пульсации и различные волны имеются и в межзвездной среде. Частицы космических лучей должны взаимодействовать с этими пульсациями (волнами), испытывать рассеяние и изменять свою энергию. Рассеяние в некоторых случаях может приводить к эффективной диффузии частиц по углам и, в конечном итоге, к изотропизации космических лучей и их диффузии в пространстве
Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Одно из основных свойств плазмы состоит в том, что в ней легко возбуждаются различные типы колебаний и волн. Турбулентные пульсации и различные волны имеются и в межзвездной среде. Частицы космических лучей должны взаимодействовать с этими пульсациями (волнами), испытывать рассеяние и изменять свою энергию. Рассеяние в некоторых случаях может приводить к эффективной диффузии частиц по углам и, в конечном итоге, к изотропизации космических лучей и их диффузии в пространстве
 Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Мы будем рассматривать рассеяние быстрых частиц при заданном спектре волн и неоднородностей. Такая постановка задачи не всегда возможна — быстрые частицы сами могут заметно изменять дисперсионные свойства плазмы и, в частности, приводить к неустойчивостям, возбуждению новых волн или, наоборот, к их затуханию.
Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Мы будем рассматривать рассеяние быстрых частиц при заданном спектре волн и неоднородностей. Такая постановка задачи не всегда возможна — быстрые частицы сами могут заметно изменять дисперсионные свойства плазмы и, в частности, приводить к неустойчивостям, возбуждению новых волн или, наоборот, к их затуханию.
 Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Если считать электрическое поле Ε и магнитное поле Н заданными, то функция распределения частиц космических лучей по импульсам f(t, r, р) определяется из кинетического уравнения (9. 1)
Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Если считать электрическое поле Ε и магнитное поле Н заданными, то функция распределения частиц космических лучей по импульсам f(t, r, р) определяется из кинетического уравнения (9. 1)
 Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Здесь Zе — заряд частицы. Нормировка функции f(t, r, р) такова, что интеграл (9. 2) дает концентрацию частиц; столкновения в (9. 1) не учитываются (na ~ 0. 1 cm-3 )
Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Здесь Zе — заряд частицы. Нормировка функции f(t, r, р) такова, что интеграл (9. 2) дает концентрацию частиц; столкновения в (9. 1) не учитываются (na ~ 0. 1 cm-3 )
 Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Далее используем обычную процедуру квазилинейного приближения, хорошо известного из физики плазмы. Разделяем поля на средние и флуктуирующие, отвечающие ансамблю волн со случайными фазами: (9. 3)
Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Далее используем обычную процедуру квазилинейного приближения, хорошо известного из физики плазмы. Разделяем поля на средние и флуктуирующие, отвечающие ансамблю волн со случайными фазами: (9. 3)
 Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Угловые скобки означают усреднение по ансамблю волн (т. е. по достаточно быстрым пульсациям). Считается, что из-за высокой проводимости среды среднее электрическое поле равно нулю (здесь предполагается, что в среде отсутствуют крупномасштабные движения). В функции распределения также выделяется флуктуирующая часть ` (9. 4) Усредняя уравнение (9. 1) по ансамблю волн, получаем
Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Угловые скобки означают усреднение по ансамблю волн (т. е. по достаточно быстрым пульсациям). Считается, что из-за высокой проводимости среды среднее электрическое поле равно нулю (здесь предполагается, что в среде отсутствуют крупномасштабные движения). В функции распределения также выделяется флуктуирующая часть ` (9. 4) Усредняя уравнение (9. 1) по ансамблю волн, получаем
 Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Подставим 9. 4 в ур-е 9. 1 и усреднив по ансамблю волн получим (9. 5) Вычитая (9. 4) из (9. 1), приходим к уравнению (9. 6)
Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Подставим 9. 4 в ур-е 9. 1 и усреднив по ансамблю волн получим (9. 5) Вычитая (9. 4) из (9. 1), приходим к уравнению (9. 6)
 Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме : Считая амплитуду волн малой (и соответственно полагая f 1 << f 0) пренебрегаем двумя последними слагаемыми в правой части уравнения (9. 6) и таким образом находим уравнение для f 1. Его решение можно представить в виде: (9. 8)
Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме : Считая амплитуду волн малой (и соответственно полагая f 1 << f 0) пренебрегаем двумя последними слагаемыми в правой части уравнения (9. 6) и таким образом находим уравнение для f 1. Его решение можно представить в виде: (9. 8)
 Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме где интегрирование проводится по траекториям частицы в поле Н 0. С помощью выражения (9. 8) из (9. 5) получаем замкнутое уравнение для усредненной функции распределения (9. 9)
Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме где интегрирование проводится по траекториям частицы в поле Н 0. С помощью выражения (9. 8) из (9. 5) получаем замкнутое уравнение для усредненной функции распределения (9. 9)
 Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Правая часть уравнения (9. 9) определяет медленное изменение функции распределения
Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Правая часть уравнения (9. 9) определяет медленное изменение функции распределения
 Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Пусть Н 0 — однородное магнитное поле, направленное вдоль оси z, а поля Е и Н 1 являются суперпозицией полей волн со случайными фазами. При этом удобно использовать представление Фурье по пространственным координатам. . (9. 10) α – тип волны.
Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Пусть Н 0 — однородное магнитное поле, направленное вдоль оси z, а поля Е и Н 1 являются суперпозицией полей волн со случайными фазами. При этом удобно использовать представление Фурье по пространственным координатам. . (9. 10) α – тип волны.
 Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Суммирование ведется по различным типам волн в плазме. Собственная частота волны каждого типа определяется дисперсионным соотношением (9. 11) Поля E и Н 1 связаны уравнением Максвелла (9. 12) Откуда: (9. 13)
Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Суммирование ведется по различным типам волн в плазме. Собственная частота волны каждого типа определяется дисперсионным соотношением (9. 11) Поля E и Н 1 связаны уравнением Максвелла (9. 12) Откуда: (9. 13)
 Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме В рассматриваемых нами задачах гирочастота — где Е полная энергия частицы, (Е 2 = р2 с2 + т2 с4) обычно так велика, что за время t ~ 1/ωH действие случайных полей Е и Н 1 слабо меняет движение быстрых частиц.
Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме В рассматриваемых нами задачах гирочастота — где Е полная энергия частицы, (Е 2 = р2 с2 + т2 с4) обычно так велика, что за время t ~ 1/ωH действие случайных полей Е и Н 1 слабо меняет движение быстрых частиц.
 Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Важнейшей особенностью взаимодействия частиц с волнами является его резонансный характер — частицы рассеиваются волнами при условии S= 0, ± 1, …. . (9. 24) ν|| и k|| - проекции волновой скорости и волнового вектора на ось z или на Н 0 Фактически соотношение это условие кратности частоты волны (с учетом эффекта доплера) частоте циклотронного вращения частицы в регулярном магнитном поле Н 0.
Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Важнейшей особенностью взаимодействия частиц с волнами является его резонансный характер — частицы рассеиваются волнами при условии S= 0, ± 1, …. . (9. 24) ν|| и k|| - проекции волновой скорости и волнового вектора на ось z или на Н 0 Фактически соотношение это условие кратности частоты волны (с учетом эффекта доплера) частоте циклотронного вращения частицы в регулярном магнитном поле Н 0.
 Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Обычно рассматривается два предельных случая. Если длина волны много меньше ларморовского радиуса частицы в регулярном магнитном поле, то можно считать, что при взаимодействии частицы движутся прямолинейно и регулярное поле Н 0 не влияет на механизм рассеяния.
Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Обычно рассматривается два предельных случая. Если длина волны много меньше ларморовского радиуса частицы в регулярном магнитном поле, то можно считать, что при взаимодействии частицы движутся прямолинейно и регулярное поле Н 0 не влияет на механизм рассеяния.
 Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Точнее, условие «незамагниченности» частиц таково: При этом взаимодействие определяется совокупностью большого числа близко расположенных гармоник при значениях: Это условие сводится к условию черенковского резонанса
Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Точнее, условие «незамагниченности» частиц таково: При этом взаимодействие определяется совокупностью большого числа близко расположенных гармоник при значениях: Это условие сводится к условию черенковского резонанса
 Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме В обратном предельном случае частицы «замагничены» . Взаимодействие идет н основном на нулевой или первой (в зависимости от поляризации волн) гармониках S= 0, ± 1.
Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме В обратном предельном случае частицы «замагничены» . Взаимодействие идет н основном на нулевой или первой (в зависимости от поляризации волн) гармониках S= 0, ± 1.
 Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Для составляющих поля волны E||α =0 значение S= 0 и условие резонанса имеет вид: Для E||α ≠ 0 значение S= ± 1 и
Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Для составляющих поля волны E||α =0 значение S= 0 и условие резонанса имеет вид: Для E||α ≠ 0 значение S= ± 1 и
 Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Для случая распространения космических лучей в межзвездной среде выполняется условие r. H << l, где l — характерная длина, на которой частицы рассеиваются на угол порядка единицы (в диффузионном приближении), а r. H=ν / |ωН| - ларморовский радиус.
Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Для случая распространения космических лучей в межзвездной среде выполняется условие r. H << l, где l — характерная длина, на которой частицы рассеиваются на угол порядка единицы (в диффузионном приближении), а r. H=ν / |ωН| - ларморовский радиус.
 Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Так, для протона с кинетической энергией Еk = 1 Гэ. В величина r. H =1012 см, а l =1018 см. Неравенство r. H << l автоматически возникает в теории рассеяния быстрых частиц в среде со слабой магнитогидродинамической турбулентностью, так что в этом смысле частицы космических лучей «замагничены» вплоть до энергий Еk ~106 Гэ. В (Еk ~ 1015 э. В ).
Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Так, для протона с кинетической энергией Еk = 1 Гэ. В величина r. H =1012 см, а l =1018 см. Неравенство r. H << l автоматически возникает в теории рассеяния быстрых частиц в среде со слабой магнитогидродинамической турбулентностью, так что в этом смысле частицы космических лучей «замагничены» вплоть до энергий Еk ~106 Гэ. В (Еk ~ 1015 э. В ).
 Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме В условиях межзвездной среды для частиц интересующих нас энергий больше нескольких сотен Мэ. В — взаимодействие с ленгмюровскими, ионно-звуковыми волнами, вистлерами и короткими (с длиной волны λ << 2π r. H) магнитогидродинамическими волнами в основном происходит за счет черенковского резонанса.
Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме В условиях межзвездной среды для частиц интересующих нас энергий больше нескольких сотен Мэ. В — взаимодействие с ленгмюровскими, ионно-звуковыми волнами, вистлерами и короткими (с длиной волны λ << 2π r. H) магнитогидродинамическими волнами в основном происходит за счет черенковского резонанса.
 Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Эффективная частота рассеяния ультрарелятивистских частиц на этих волнах уменьшается с ростом энергии как Е-2 , поэтому в межзвездной среде такое рассеяние не может играть большой роли. Действительно, наблюдается лишь слабая зависимость времени выхода космических лучей из Галактики от энергии Т ~ Е-μ , μ = 0, 3 ÷ 0, 5 и, следовательно, рассеяние с частотой, пропорциональной Е-2, не имеет места.
Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Эффективная частота рассеяния ультрарелятивистских частиц на этих волнах уменьшается с ростом энергии как Е-2 , поэтому в межзвездной среде такое рассеяние не может играть большой роли. Действительно, наблюдается лишь слабая зависимость времени выхода космических лучей из Галактики от энергии Т ~ Е-μ , μ = 0, 3 ÷ 0, 5 и, следовательно, рассеяние с частотой, пропорциональной Е-2, не имеет места.
 Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме При рассеянии на магнитогидродинамических волнах с длиной волны λ ~ 2π r. H положение иное. Зависимость эффективной частоты рассеяния от энергии не универсальна и определяется видом спектра волн. Для простоты будем считать (хотя это не всегда верно в условиях межзвездной среды), что скорость звука в среде много меньше альфвеновской скорости νs << νa
Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме При рассеянии на магнитогидродинамических волнах с длиной волны λ ~ 2π r. H положение иное. Зависимость эффективной частоты рассеяния от энергии не универсальна и определяется видом спектра волн. Для простоты будем считать (хотя это не всегда верно в условиях межзвездной среды), что скорость звука в среде много меньше альфвеновской скорости νs << νa
 Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме (k — постоянная Больцмана, Те — температура тепловых электронов, тi — масса ионов в плазме) (ρ — плотность среды).
Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме (k — постоянная Больцмана, Те — температура тепловых электронов, тi — масса ионов в плазме) (ρ — плотность среды).
 Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Тогда в магнитогидродинамической области, т. е. при ω << ωНi (ωНi =Zi. H/mic) существуют две ветви колебаний: альфвеновские волны с дисперсионным соотношением и (быстрые) магнитозвуковые волны, для которых
Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Тогда в магнитогидродинамической области, т. е. при ω << ωНi (ωНi =Zi. H/mic) существуют две ветви колебаний: альфвеновские волны с дисперсионным соотношением и (быстрые) магнитозвуковые волны, для которых
 Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме В альфвеновскпх волнах скорость среды направлена перпендикулярно волновому вектору k и внешнему полю Н 0, а электрическое поле лежит в плоскости k , Н 0. Групповая скорость этих волн νгр = νа Н 0 / Н
Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме В альфвеновскпх волнах скорость среды направлена перпендикулярно волновому вектору k и внешнему полю Н 0, а электрическое поле лежит в плоскости k , Н 0. Групповая скорость этих волн νгр = νа Н 0 / Н
 Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме В магнитозвуковых волнах колебания скорости среды лежат в плоскости векторов k и Н 0, а электрическое поле направлено перпендикулярно этой плоскости. Групповая скорость магнитозвуковых волн νгр = νа k / |k|.
Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме В магнитозвуковых волнах колебания скорости среды лежат в плоскости векторов k и Н 0, а электрическое поле направлено перпендикулярно этой плоскости. Групповая скорость магнитозвуковых волн νгр = νа k / |k|.
 Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме В межзвёздной среде при Н 0 = 5 10 -6 Э и концентрации газа n = 0, 1 см-3 альфвеновская скорость νа = 5 10 -6 см/с. При распространении вдоль магнитного поля альфвеновская и магнитозвуковая волны представляют собой две поперечные противоположно циркулярно поляризованные волны, распространяющиеся с альфвеновской скоростью.
Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме В межзвёздной среде при Н 0 = 5 10 -6 Э и концентрации газа n = 0, 1 см-3 альфвеновская скорость νа = 5 10 -6 см/с. При распространении вдоль магнитного поля альфвеновская и магнитозвуковая волны представляют собой две поперечные противоположно циркулярно поляризованные волны, распространяющиеся с альфвеновской скоростью.
 Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Приближение замагниченных частиц в данном случае строго выполняется лишь для волн, распространяющихся вдоль магнитного поля, кроме этого, волны с k┴ ≠ 0 сильно затухают. Поэтому будем рассматривать случаи распространения волн вдоль регулярного магнитного поля Н 0.
Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Приближение замагниченных частиц в данном случае строго выполняется лишь для волн, распространяющихся вдоль магнитного поля, кроме этого, волны с k┴ ≠ 0 сильно затухают. Поэтому будем рассматривать случаи распространения волн вдоль регулярного магнитного поля Н 0.
 Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Введём цилиндрическую систему координат, тогда p┴ и p║ - перпендикулярная и параллельная составляющие импульса относительно оси z, θ - питч-угол, т. е. угол между р и Н 0. Введём обозначение μ = cos θ. φ – азимутальный угол
Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Введём цилиндрическую систему координат, тогда p┴ и p║ - перпендикулярная и параллельная составляющие импульса относительно оси z, θ - питч-угол, т. е. угол между р и Н 0. Введём обозначение μ = cos θ. φ – азимутальный угол
 Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Будем использовать усреднённую по углу φ функцию распределения (9. 14)
Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Будем использовать усреднённую по углу φ функцию распределения (9. 14)
 Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме От переменных p┴ и p║ перейдём к p = │p│, k = k ║, μ и Условие резонанса (9. 24) имеет вид
Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме От переменных p┴ и p║ перейдём к p = │p│, k = k ║, μ и Условие резонанса (9. 24) имеет вид
 Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Уравнение (9. 9) теперь сводится к следующему
Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Уравнение (9. 9) теперь сводится к следующему
 Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Величина плотность энергии волн типа α со случайными фазами и случайным распределением поляризаций. Для альфвеновских и магнитозвуковых волн энергия волн поровну распределена между кинетической энергией частиц среды и энергией магнитного поля
Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Величина плотность энергии волн типа α со случайными фазами и случайным распределением поляризаций. Для альфвеновских и магнитозвуковых волн энергия волн поровну распределена между кинетической энергией частиц среды и энергией магнитного поля
 Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Уравнение (9. 28) показывает, что частицы быстро рассеиваются по углам, но медленно меняют свою энергию, поскольку производные входят с большими множителями Это обстоятельство позволяет пренебречь ускорением частиц и учитывать только диффузию по углам.
Рассеяние быстрых частиц в слаботурбулентной магнитоактивной плазме Уравнение (9. 28) показывает, что частицы быстро рассеиваются по углам, но медленно меняют свою энергию, поскольку производные входят с большими множителями Это обстоятельство позволяет пренебречь ускорением частиц и учитывать только диффузию по углам.
 Диффузионное приближение Релаксация анизотропного распределения определяется эффективной частотой рассеяния частиц на волнах, которую в соответствии с уравнением (9. 28) для одного типа волн α удобно определить как
Диффузионное приближение Релаксация анизотропного распределения определяется эффективной частотой рассеяния частиц на волнах, которую в соответствии с уравнением (9. 28) для одного типа волн α удобно определить как
 Диффузионное приближение θ - питч-угол, т. е. угол между р и Н 0, а μ = cos θ. Характерное время изотропизации (или время рассеяния частицы на угол порядка единицы) равно оно зависит от гирочастоты рассеиваемой частицы и относительной плотности энергии волн в резонансной области (по сравнению с энергией регулярного поля). Напомним, что используется приближение слабой турбулентности, так что.
Диффузионное приближение θ - питч-угол, т. е. угол между р и Н 0, а μ = cos θ. Характерное время изотропизации (или время рассеяния частицы на угол порядка единицы) равно оно зависит от гирочастоты рассеиваемой частицы и относительной плотности энергии волн в резонансной области (по сравнению с энергией регулярного поля). Напомним, что используется приближение слабой турбулентности, так что.
 Диффузионное приближение В зависимости от вида спектра частота может иметь разную зависимость от энергии частиц и, в частности, при ~ k-2 величина не зависит от энергии в ультрарелятивистской области.
Диффузионное приближение В зависимости от вида спектра частота может иметь разную зависимость от энергии частиц и, в частности, при ~ k-2 величина не зависит от энергии в ультрарелятивистской области.
 Диффузионное приближение При t >> и расстояниями, много большими длины релаксации l >> v , можно ожидать, что функция распределения имеет вид где анизотропная добавка мала , а
Диффузионное приближение При t >> и расстояниями, много большими длины релаксации l >> v , можно ожидать, что функция распределения имеет вид где анизотропная добавка мала , а
 Диффузионное приближение После усреднения уравнения (9. 28) по косинусу питч-угла получаем замкнутое уравнение для f 0 с точностью до (9. 37) Здесь эффективная скорость конвективного переноса частиц волнами равна
Диффузионное приближение После усреднения уравнения (9. 28) по косинусу питч-угла получаем замкнутое уравнение для f 0 с точностью до (9. 37) Здесь эффективная скорость конвективного переноса частиц волнами равна
 Диффузионное приближение После усреднения уравнения (9. 28) по косинусу питч-угла получаем замкнутое уравнение для f 0 с точностью до (9. 37)
Диффузионное приближение После усреднения уравнения (9. 28) по косинусу питч-угла получаем замкнутое уравнение для f 0 с точностью до (9. 37)
 Диффузионное приближение Пространственный коэффициент диффузии вдоль регулярного поля Но дается соотношением коэффициент диффузии по модулю импульса, определяющий статистическое ускорение частиц, равен
Диффузионное приближение Пространственный коэффициент диффузии вдоль регулярного поля Но дается соотношением коэффициент диффузии по модулю импульса, определяющий статистическое ускорение частиц, равен
 Диффузионное приближение В общем случае рассеянно частиц на волнах приводит к их пространственной диффузии, конвективному переносу, сопровождающемуся регулярным (называемым адиабатическим) изменением энергии в неоднородном потоке, и статистическому ускорению. При условии - отсутствует конвективный перенос, а при условии нет статистического ускорения
Диффузионное приближение В общем случае рассеянно частиц на волнах приводит к их пространственной диффузии, конвективному переносу, сопровождающемуся регулярным (называемым адиабатическим) изменением энергии в неоднородном потоке, и статистическому ускорению. При условии - отсутствует конвективный перенос, а при условии нет статистического ускорения
 Оценка коэффициента диффузии КЛ в галактике Предположим, что спектр волн имеет степенной вид: где Н 1┴ — средняя перпендикулярная к регулярному полю компонента случайного поля в основном масштабе тогда при (9. 48)
Оценка коэффициента диффузии КЛ в галактике Предположим, что спектр волн имеет степенной вид: где Н 1┴ — средняя перпендикулярная к регулярному полю компонента случайного поля в основном масштабе тогда при (9. 48)


