Volume Volatility and Stock Return on the Romanian

Volume, Volatility and Stock Return on the Romanian Stock Market Dissertation paper MSc Student: Valentin STANESCU Supervisor: Professor Moisa ALTAR

Previous research about volume Lamorieux and Laplace (1991) 4 Gallant, Rossi and Tauchen (1992) 4 Karpoff (1987) 4 • 4 Rogalsky (1978), Smirlock and Starks (1988), Jain and Joh (1988) and Antoniewicz (1992) • 4 contemporaneous stock price-volume relation traditional Granger causality tests Baek and Brock (1992), Hiemstra and Jones (1993, 1994) • nonlinear Granger tests

The Data 4 Estimation and training: • 4 953 observations 16/6/1997 until 2/08/2001 test data: • 200 from 3/08/2001 until 1/7/2002 Eliminated non trading days 4 Volume = no. of shares 4 Price = closing price 4 Volume precedes price 4

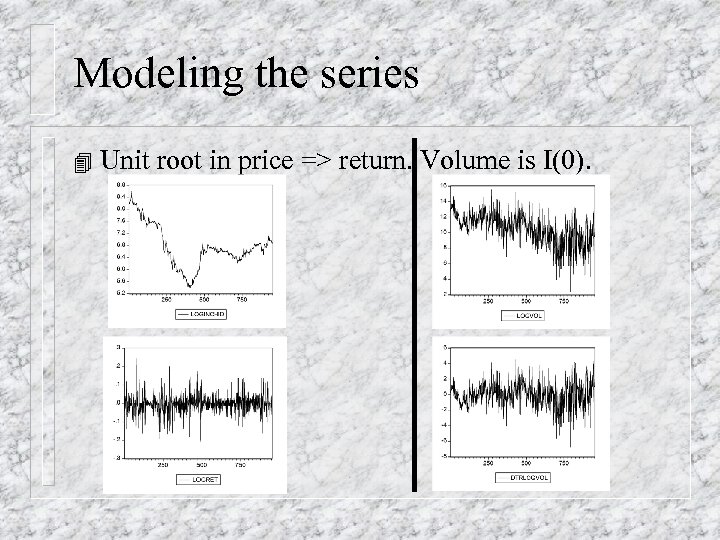Modeling the series 4 Unit root in price => return. Volume is I(0).

Detrended volume Long term analysis is not a goal of the paper Short term trend might contain relevant information

Unit root tests: ADF, price

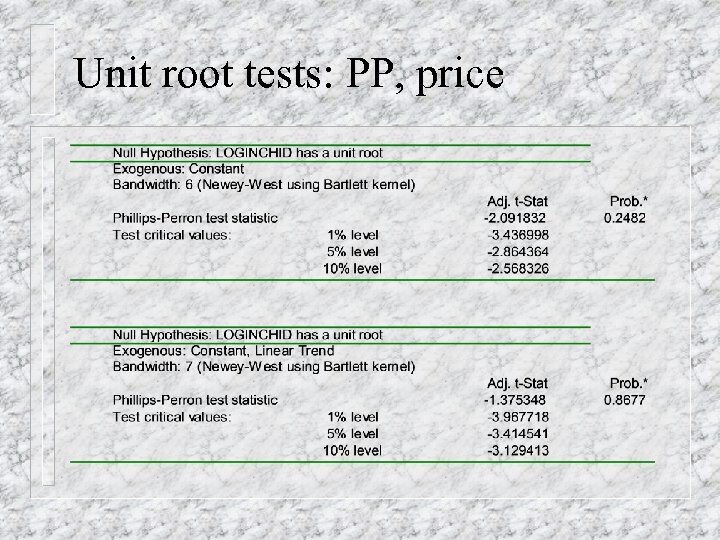Unit root tests: PP, price

Unit root tests: return

Unit root tests: volume

GARCH equation for the return Note the persistence in volatility

Zooming in. . . Notice how the volume spikes up when the volatility increases Sometimes the reaction of the volume follows the increase of the volatility (continuous line) but sometimes it precedes the turbulent period (dotted line). Is there a link between the two?

Linear Granger tests, volume vs variance and vs return Volume causes the variance but there is no linear relation to the return

Explanations for causality 4 the sequential information arrival models • 4 tax and non-tax related motives for trading • 4 Lakonishok and Schmidt (1989) mixture of distributions models • 4 Copenland (1976), Jennings, Starks and Fellingham (1981) Clark (1973) and Epps (1976) noise trader models • • not based on fundamentals stock returns are positively autocorrelated in the short run, but negatively autocorrelated in the long run

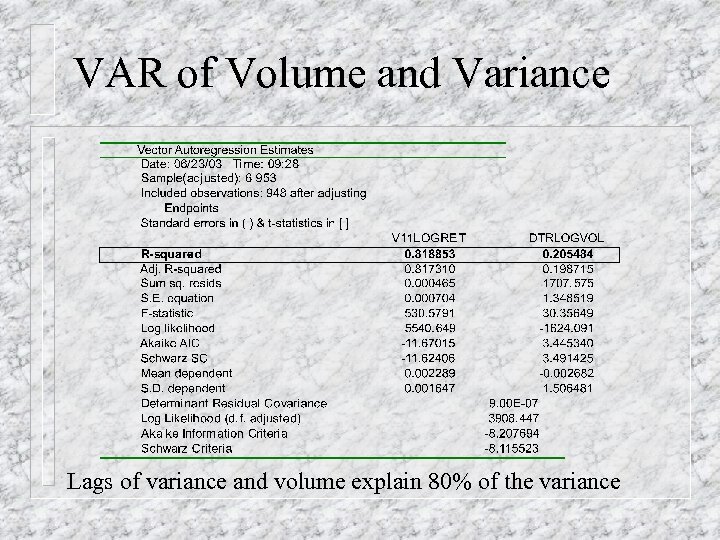VAR of Volume and Variance Lags of variance and volume explain 80% of the variance

Volume in variance equation There is no more persistence in volatility

Model for volume

Dummies for volume Significant coefficients but small and irrelevant R squared.

Implications 4 4 4 return variance was slowly adjusted because of the persistence, now it is volume dependent mean return is still set to zero because of a lack of a better prediction the volume has a AR mean equation which leads to a predictable value, unlike the return’s return variance is forecasted instead of adapted Applications • Risk management • Option strategies • Delta hedged portfolio • Other strategies involving the volatility

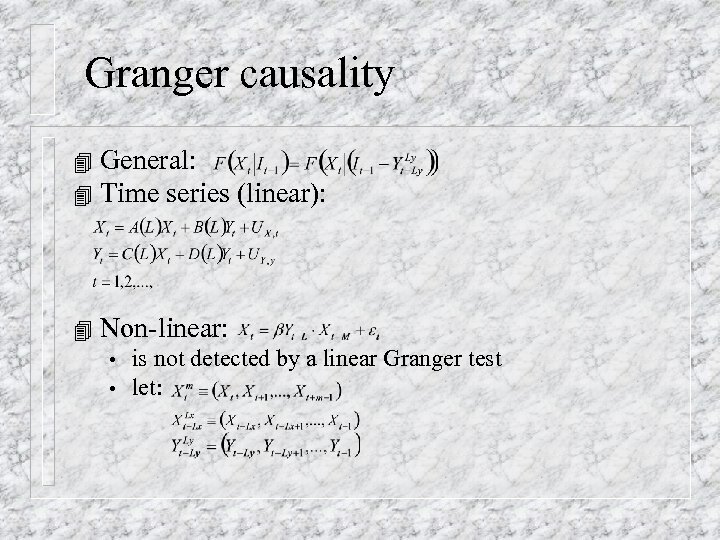Granger causality General: 4 Time series (linear): 4 4 Non-linear: • • is not detected by a linear Granger test let:

Non-linear causality 4 Testable implication: 4 we note:

Statistic 4 Statistic: 4 Estimated:

Estimation 4 Variance: • d(n) = { 1/C 2(Lx, Ly, e, n) , -C 1(m+Lx, Ly, e, n)/C 22(Lx, Ly, e, n) , 1/C 4(Lx, e, n) , C 3(m+Lx, e, n)/C 42(Lx, e, n) }

Nonlinear Granger test 4 4 4 Linear VAR residuals of simple GARCH filtered returns and of volume factor GARCH filtered returns, scaled to share a common standard deviation of 1 and thus a common scale factor e. Heuristic approach to find “the needle in the hay stack”. 10% statistically significant causality from volume to return in both cases for T=952, m=1, Lx=8, Ly=6 and e=0. 3 Insignificant results for a relation running from returns to volume Problems: • • how to determine the remaining relations? is the relation always present?

Fuzzy logic and neural networks 4 Classic algebra 4 Patched function • • • subsets noise resistant triangles are probabilities Explicit rules 4 Internal significance test 4

The internal mechanism 4 The fuzzy logic neural network does not extract all the possible rules and assign probabilities to them, instead it tries to • 4 4 increase or decrease the degree of a fuzzy variable, the number of sets, the location of the set separator, the links between the subnetworks and the variables and the probabilities. The degree of a variable is the number of sets it can belong to The number of sets is adjusted and the center of all the sets is moved to minimize their cumulated distance to the observations For each required output a network is created and they are trained simultaneously By changing the connections between the inputs and the subnetworks of a network an input may be found to be irrelevant to a certain output.

The information set and targets 4 The information set considers the parameters where the nonlinear Granger test indicated causality: • eight lags of the return, absolute return, and squared return • current and six lags of volume • alternate set that included the price 4 Targets: • • • current return, absolute return, squared return buy decision, buy/sell decision volume (adjusted information set)

Results 4 Failure. . . to model: • • • current return buy decision buy/sell decision Weird results for price => discarded 4 Success: 4 • • • 4 absolute returns squared returns volume All the variables had a degree of two showing that they belonged to just two subsets.

Squared return 4 Relevant information: • 4 Rules extracted • • 4 volume and 1 lag squared return, divided in two subsets if volume is small then squared return will almost surely be small if volume is large then squared return will almost surely be large This confirms the econometric results in which volume was linked to volatility as in Lamourieux and Laplace (1991) and Clark’s models.

Absolute returns 4 Relevant information: • 4 Rules extracted: if volume is small then absolute return will be almost surely small • if volume is large then absolute return will be small with 32% probability or large with 68% probability • if the 1 lag absolute return is small then the current absolute return will be small with 72% probability or large with 28% probability • if the 1 lag absolute return is large then the current absolute return will almost surely be large Rule 1 and the second part of rule 2 show a positive correlation between volume and absolute return but the first part indicates the possibility of a negative correlation. This result is consistent with the sequential information arrival models of Copeland (1976) and Jennings, Starks and Fellingham (1981). • 4 1 lag absolute return and volume, both with two subsets

Volume 4 4 Relevant information: two lags of volume Rules extracted: • • 4 if the first lagged volume is small then surely be small if the first lagged volume is large then surely be large if the second lag is small then current probability or large with 23% probability if the second lag is large then current probability or large with 88% probability the current volume will almost value will be small with 77% value will be small with 12% These rules only confirm the autoregressive in mean, heteroskedastic, with persistence in variance estimated TARCH model, but only the first two lags were deemed relevant. It may be that the volume depends on other factors like the speed of information flow from Clark’s model.

Evaluating the network 4 4 Just for the absolute and squared returns, and volume The network performs its own internal tests when deciding whether to drop a rule, a subnetwork or make other adjustments. If the new configuration is better at explaining the data then the components added were significant and those removed had little explanatory power. When evaluating the network on the last 200 observations these internal mechanisms showed that the network performed well on data not presented to it in the training stages.

Conclusions and remarks 4 4 In line with the empirical results obtained in the literature on the stock price-volume relation by indicating the presence of a nonlinear Granger causality between closing prices and volume. Suggests that researchers should consider nonlinear theoretical mechanisms and empirical regularities when devising and evaluating models of the joint dynamics of stock prices and trading volume. Or the fact that they could be related through different functions for each subset. No guidance regarding the source or form of the nonlinear dependence. The relation between return, variance and volume was partially modeled but the process governing the volume could not be modeled better than using a GARCH model. This could be an interesting goal for future research.

References 4 4 4 4 4 Andersen, T. (1992), Return volatility and trading volume in financial markets: An information flow interpretation of stochastic volatility, Working paper, Northwestern University Antoniewicz, R. (1992), A causal relationship between stock returns and volume, Working paper, Federal Reserve Board Baek, E. and W. Brock (1992), A general test for nonlinear Granger causality: Bivariate model, Working paper, Iowa State University and University of Wisconsin, Madison Berndt, E. , B. Hall, and J. Hausman (1974), Estimation and inference in nonlinear structural models, Annals of Economic and Social Measurement 3, 653 -665 Brock, W. , D. Hsieh, and B. Le. Baron (1991), A Test of Nonlinear Dynamics, Chaos, and Instability: Statistical Theory and Economic Evidence, MIT Press, Cambridge. Campbell, J. , S. Grossman, and J. Wang (1993), Trading volume and serial correlation in stock returns, Quarterly Journal of Economics 108, 905 -939 Clark, P. (1973), A subordinated stochastic process model with finite variances for speculative prices, Econometrica 41, 135 -155 Copeland T. (1976), A model of asset trading under the assumption of sequential information arrival, Journal of Finance 31, 135 -155 Dikerson, J, and B. Kosko (1996), Fuzzy function approximation with ellipsoidal rules, IEEE Transations on systems, man, and cybernetics – part B: Cybernetics, vol 26, no. 4 Duffe, G. (1992), Trading volume and return reversals, Working paper, Federal Reserve Board

References 4 4 4 4 4 Engle, R. (1982) Autoregressive conditional heteroskedasticity with estimates of the variance of the United Kingdom inflation, Econometrica 50, 987 -1007 Epps, T. , and M. Epps (1976), The stochastic dependence of security price changes and transaction volumes: Implications for the mixture of distributions hypothesis, Econometrica 44, 305 -321 Fama, E. , and K. French (1988), Permanent and temporary components of stock prices, Journal of Political Economy 96, 246 -273 Gallant, R. , P. Rossi, and G. Tauchen (1992 a), Stock prices and volume, Review of Financial Studies 5, 199 -242 (1992 b), Nonlinear dynamic structures, Econometrica 61, 871 -907 Hiemstra, C. , and J. Jones (1992), Detection and description of linear and nonlinear dependence in daily Dow Jones stock returns and NYSE trading volume, Working paper, University of Strathclyde and Securities and Exchange Commission Hinich, M. and D. Patterson, (1985), Evidence of nonlinearity in stock returns, Journal of Business and Economic Statistics 3, 69 -77 Hsieh, D. (1991), Chaos and nonlinear dynamics: Application to financial markets, Journal of Finance 46, 1839 -1877 Jain, P. and G. Joh (1988), The dependence between hourly prices and trading volume, Journal of Financial and Quantitative Analysis 23, 269 -283

References 4 4 4 4 4 Jennings, R. , L. Starks, and J. Fellingham (1981), An equilibrium model of asset trading with sequential information arrival, Journal of Finance 36, 143 -161 Karpoff, J. (1987), The relation between price changes and trading volume: A survey, Journal of Financial and Quantitative Analysis 22, 109 -126 Kosko, B. (1988), Bidirectional Associative Memory, IEEE Transactions on systems, man and cybernetics, vol. 18, no. 1 Kosko, B. (1990 a), Unsupervised learning in noise, IEEE Transactions on neural networks, vol. 1, no. 1 Kosko, B. , and S. Mitaim (1997), Adaptive stochastic resonance, IEEE Transactions on neural networks Lakonishok, J. , and S. Smidt (1989), Past price changes and current trading volume, The Journal of Portfolio Management 15, 18 -24 Lamoureux, C. , and W. Lastrapes (1990), Heteroskedasticity in stock return data: Volume versus GARCH effects, Journal of Finance 45, 221 -229 Scheinkman, J. , and B. Le. Baron (1989), Nonlinear dynamics and stock returns, Journal of Business 62, 311 -337 White, H. (1980), A heteroscedasticity-consistent covariance matrix estimator and a direct test for heteroskedasticity, Econometrica 48, 817 -838