Волоконная оптика лекция1.ppt
- Количество слайдов: 39

ВОЛОКОННАЯ ОПТИКА КУРС ЛЕКЦИЙ Направление подготовки бакалавров 200600 ФОТОНИКА И ОПТОИНФОРМАТИКА В. М. Шандаров Томский государственный университет систем управления и радиоэлектроники

Распределение учебного времени n n Лекции - 40 часов Лабораторные занятия - 12 часов Самостоятельная работа - 28 часов Всего - 80 часов
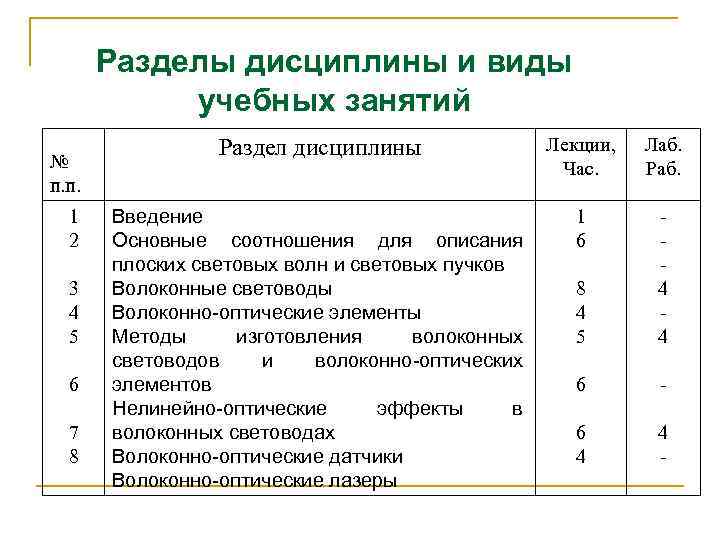
Разделы дисциплины и виды учебных занятий № п. п. 1 2 3 4 5 6 7 8 Раздел дисциплины Лекции, Час. Лаб. Раб. Введение Основные соотношения для описания плоских световых волн и световых пучков Волоконные световоды Волоконно-оптические элементы Методы изготовления волоконных световодов и волоконно-оптических элементов Нелинейно-оптические эффекты в волоконных световодах Волоконно-оптические датчики Волоконно-оптические лазеры 1 6 8 4 5 4 4 6 - 6 4 4 -

Методические материалы n n n n n Методические материалы по дисциплине «Волоконная оптика» : S: //Шандаров В. М. /33 УМК Волоконная оптика 200600 2 Раб прогр Вол оптика 2012. DOC 4 Уч пос ВОУи. СТН 2012. pdf 5 Лаб раб 1. pdf 5 Лаб раб 2. pdf 5 Лаб раб 3. pdf 6 ВОУи. СТН задачи 2012. pdf 7 Вопросы к зачету. DOC

Рекомендуемая литература n Основная литература: n n 1. Фриман, Роджер. Волоконно-оптические системы связи : Пер. с англ. / Р. Фриман ; ред. пер. Н. Н. Слепов. - 3 -е изд. , доп. - М. : Техносфера, 2006. - 495[1] с. : ил. , табл. - (Мир связи ; IX-03). (14) 2. В. М. Шандаров. Волоконно-оптические устройства технологического назначения: учеб. пособие. – Томск : Томск. гос. ун-т систем упр. и радиоэлектроники, 2007. – 190 с. ISBN 978 -586889 -377 -3. (40) n Дополнительная литература: n 1 д. А. Ярив, П. Юх. Оптические волны в кристаллах. - М. : Мир, 1987. - 616 с. 2 д. Ю. Н. Кульчин. Распределенные волоконно – оптические измерительные системы. – М. : Физматлит, 2001 г. , 272 с. 3 д. В. М. Шандаров. Основы физической и квантовой оптики. – Томск: Томск. гос. Ун-т систем упр. и радиоэлектроники, 2005. – 258 с. (20) n n

Введение (1 час) n Цель дисциплины состоит в ознакомлении студентов с физическими принципами функционирования, типовыми схемами построения, технологией изготовления современных волоконно-оптических и интегральнооптических элементов и устройств. n В рамках дисциплины изучаются фундаментальные положения оптики диэлектрических волноводов, методы модуляции параметров световых волн в волоконнооптических элементах, особенности проявления нелинейнооптических эффектов в волоконных световодах, методы изготовления волоконных световодов, основные принципы построения волоконно-оптических устройств и приборов.

Почти волоконная оптика… n Свет может расцвечивать водяные струи – это давно было отмечено и сейчас широко используется. Стекловолоконные жгуты нашли применение и в эндоскопии еще до изобретения лазера. Но без лазеров волоконная оптика не появилась бы… 1966 г. – предложено использовать стекловолокно для передачи оптических сигналов
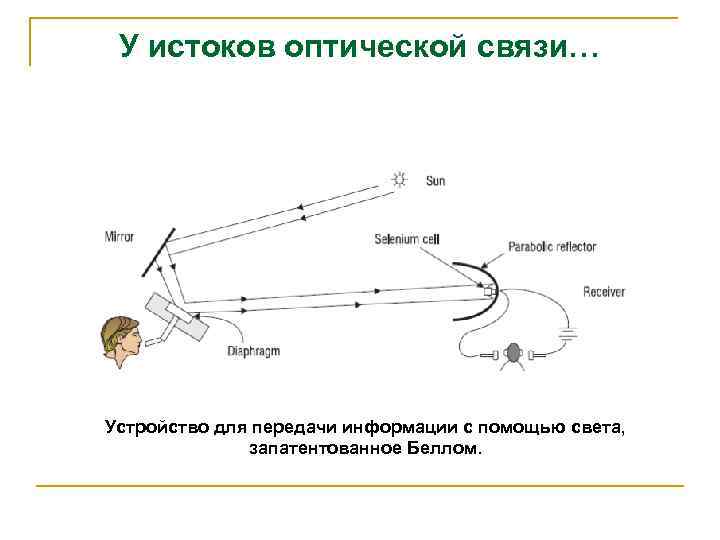
У истоков оптической связи… Устройство для передачи информации с помощью света, запатентованное Беллом.

Они «приложили руку» к становлению волоконной оптики (соотечественники) А. М. Прохоров лауреат Нобелевской премии Е. М. Дианов академик, директор Научного центра волоконной оптики при Институте общей физики РАН

Основные области применения волоконной оптики n n n Волоконно-оптические линии связи Волоконные лазеры Волоконно-оптические датчики

Основные положения и допущения Вещество - сплошная среда с некоторыми макроскопическими электродинамическими параметрами , , ; n Для представления физических величин используется международная система единиц (СИ), что определяет форму записи уравнений Максвелла и некоторых других соотношений; n Световое (электромагнитное) поле характеризуется четырьмя векторными величинами: - напряженность электрического поля (В/м); - электрическая индукция (Кл/м 2); - напряженность магнитного поля (A/м); - магнитная индукция (Вб/м 2); Сила, действующая на пробный электрический заряд: n

Уравнения Максвелла в интегральной форме Джеймс Клерк Максвелл (1831 -79) — английский физик, создатель классической электродинамики. Уравнения Максвелла — основные уравнения классической макроскопической электродинамики, описывающие электромагнитные явления в произвольных средах и в вакууме. Уравнения Максвелла получены Дж. К. Максвеллом в 60 -х гг. 19 в. в результате обобщения найденных из опыта законов электрических и магнитных явлений. Закон Ампера о полном токе (сформулирован на основе экспериментов Эрстеда) Закон электромагнитной индукции Фарадея Закон Гаусса о потоке вектора электрической индукции Закон о потоке вектора магнитной индукции

Уравнения Максвелла в дифференциальной форме Соотношения между дифференциальными и интегральными характеристиками ЭМП: Ток I, протекающий через некоторое сечение это поток вектора плотности тока через данное сечение Электрический заряд q в некоторой области может быть выражен в виде объемного интеграла от объемной плотности заряда в данной области Магнитный поток через площадку, ограниченную некоторым контуром, представляется потоком вектора магнитной индукции через эту площадку

Переход n Для: n Согласно теореме Стокса, левая часть этого соотношения преобразуется к виду: n равенство выполняется для произвольной поверхности S и из него вытекает равенство подынтегральных выражений:

Ток смещения n В дополнение к току проводимости, Максвелл ввел в рассмотрение ток смещения, не связанный с движением электрических зарядов, а характеризующий прохождение переменного тока по цепи, содержащей емкости. При этом

Уравнения Максвелла в дифференциальной форме 1) 2) От интегральной к дифференциальной форме уравнений Максвелла можно перейти, используя формулы Остроградского – Гаусса и Стокса 3) 4) 1 а) 2 а) Для световых волн в диэлектрической среде

Материальные уравнения n n n Материальные уравнения учитывают влияние среды, в которой распространяется свет, на связь между векторами поля. Такая связь определяется микроскопическими свойствами среды, т. е. ее атомно – молекулярной структурой. Выявить характер связи аналитическим путем принципиально возможно, но на практике - почти невозможно. Для учета влияния среды используют феноменологический подход, т. е. вводят макроскопические параметры, определяющие связь между векторами поля в веществе. Это диэлектрическая проницаемость и магнитная проницаемость , а также удельная проводимость среды . Их численные значения, как правило, находятся экспериментальным путем.
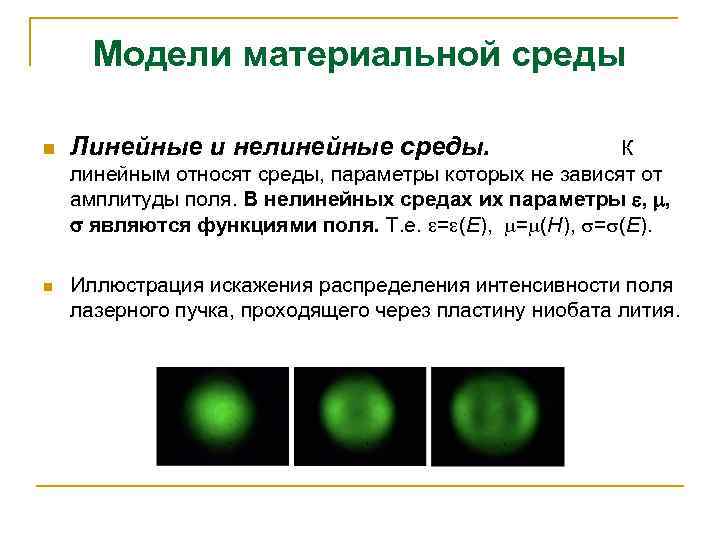
Модели материальной среды n n Линейные и нелинейные среды. К линейным относят среды, параметры которых не зависят от амплитуды поля. В нелинейных средах их параметры e, m, s являются функциями поля. Т. е. = (E), = (H), = (E). Иллюстрация искажения распределения интенсивности поля лазерного пучка, проходящего через пластину ниобата лития.
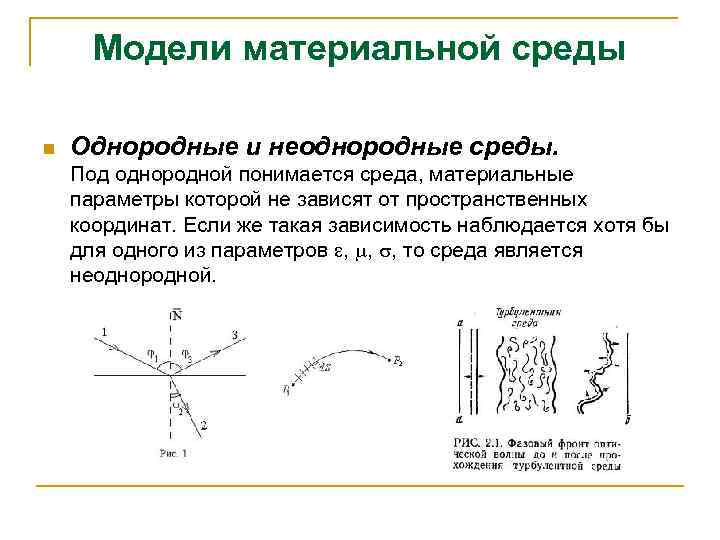
Модели материальной среды n Однородные и неоднородные среды. Под однородной понимается среда, материальные параметры которой не зависят от пространственных координат. Если же такая зависимость наблюдается хотя бы для одного из параметров , , , то среда является неоднородной.
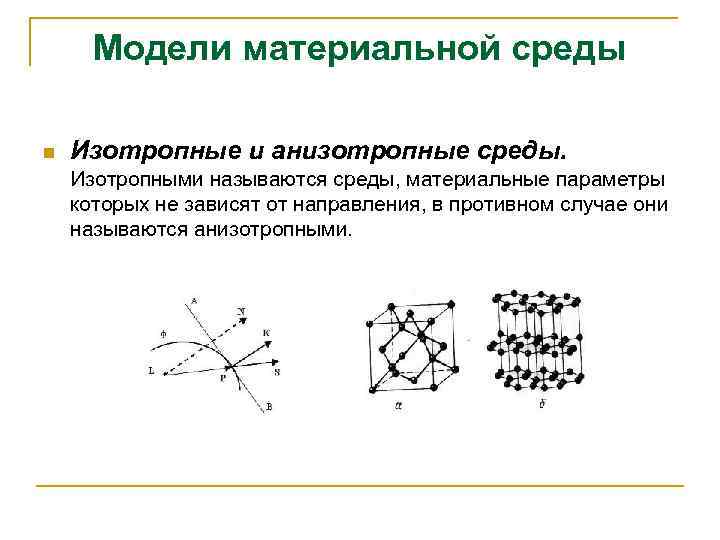
Модели материальной среды n Изотропные и анизотропные среды. Изотропными называются среды, материальные параметры которых не зависят от направления, в противном случае они называются анизотропными.

Модели материальной среды n Среды с пространственной и временной дисперсией. О дисперсии говорят в случае нелокального отклика среды на воздействие. Под нелокальным откликом понимается ситуация, когда значение вектора (или ) в данной точке пространства в данный момент времени может зависеть от значения (или ) в предыдущие моменты времени либо в других точках пространства.

Соотношения между векторами поля. Вакуум. n n В этом случае для определения поля достаточно двух векторов: и. Остальные задаются соотношениями: где 0 - универсальная электрическая постоянная (или диэлектрическая проницаемость вакуума) 0=8, 85 1012=(1/36 ) 10 -9 Ф/м; - универсальная магнитная постоянная 0 (магнитная проницаемость вакуума) - 0=4 10 -7 Гн/м.

Изотропная среда n Материальные уравнения для изотропной среды имеют вид: - вектор поляризации среды; - намагниченность среды; - диэлектрическая восприимчивость; M - магнитная восприимчивость среды; , - абсолютные диэлектрическая и магнитная проницаемости.

Изотропная среда n В отсутствие электрического поля все атомы и молекулы вещества электрически нейтральны. Под действием поля орбиты электронов (с позиций классической физики) деформируются, центры “тяжести” положительного и отрицательного зарядов в атоме смещаются в направлении поля в разные стороны. В итоге атом может быть представлен в виде электрического диполя. То же можно сказать о молекулах вещества, не имеющих собственного дипольного момента. Если молекулы имеют собственный дипольный момент, то в отсутствие поля они ориентированы в пространстве хаотично. Под действием поля они ориентируются вдоль его направления. Таким образом, в электрическом поле атом или молекула могут характеризоваться дипольным моментом , где q - величина электрического заряда, l - расстояние между “центрами тяжести” разноименных зарядов, единичный вектор в направлении от отрицательного заряда к положительному. Степень поляризации вещества определяется вектором поляризации , который численно равен дипольному моменту единицы объема вещества: , N –число диполей в единице объема.

Изотропная среда n При не очень сильных полях ~ и это соотношение можно представить в виде , где величину называют диэлектрической восприимчивостью. Соответственно, поле в веществе характеризуют вектором , определяемым выражением Аналогичным образом вводится и соотношение для вектора магнитной индукции, при выводе которого учитывается, что атомы или молекулы вещества могут иметь собственный магнитный момент.

Анизотропная среда n n Анизотропия физических свойств вещества является следствием упорядоченности его микроструктуры и существованием, в связи с этим, некоторых выделенных направлений. Связь между векторами электромагнитного (светового) поля в этом случае более сложна, т. к. физические свойства вещества не являются скалярными величинами, а описываются тензорами. В анизотропной среде векторы и (или и ) могут быть непараллельными. Так, для компонент вектора можно записать следующие соотношения: Здесь ij - компоненты тензора диэлектрической проницаемости (тензор второго ранга).

Анизотропная среда n n Для краткости эти соотношения записываются в виде , где по повторяющимся индексам проводится суммирование. В анизотропной среде тензор может быть приведен к диагональному виду, когда отличны от нуля лишь его компоненты xx, yy, zz. Соответствующая система координат называется главными осями тензора. Аналогичные соотношения можно записать для компонент вектора магнитной индукции в магнитно - анизотропной среде: здесь ij - компоненты тензора абсолютной магнитной проницаемости.

Среды с пространственной и временной дисперсией n В этом случае связь между векторами поля оказывается еще более сложной, поскольку необходим учет нелокальности и инерционности процесса поляризации среды. Вид этой связи зависит от геометрии тела и характеристик процесса в предыдущие моменты времени.

Деление сред по диэлектрическим и магнитным свойствам n n К числу материальных уравнений можно отнести и закон Ома в дифференциальной форме: В зависимости от величины все среды делятся на проводники, полупроводники и диэлектрики. Величина относительной диэлектрической проницаемости r>1. Для сегнетоэлектриков r может достигать нескольких тысяч. По магнитным свойствам все материалы делят на диамагнетики ( r<1), парамагнетики ( r>1) и ферромагнетики ( r>>1).
Уравнения граничных условий n Уравнения Максвелла совместно с материальными уравнениями описывают электромагнитное (световое) поле в безграничной среде. В реальных случаях области определения поля содержат границы раздела сред с различными электродинамическими параметрами. Поэтому для выяснения конкретного вида решений электродинамических задач необходимо знать законы изменения векторов поля на границах раздела. Такие законы задаются уравнениями граничных условий. Запишем их отдельно для нормальных и тангенциальных составляющих векторов поля на границе, т. к. возможно представление любого вектора в виде суммы двух (или произвольного числа) других векторов.

Уравнения граничных условий n Граничные условия для нормальных компонент или D 1 n - D 2 n = n Граничные условия для тангенциальных компонент или E 1 t=E 2 t n Для случая свободной от электрического заряда границы D 2 n = D 1 n ; E 1 t = E 2 t ; D 2 t = ( 2/ 1)D 1 t E 2 n = ( 1/ 2)E 1 n

Граничные условия для векторов магнитного поля n B 1 n = B 2 n; n H 1 t = H 2 t H 1 n = ( 2/ 1) H 2 n B 2 t = ( 2 / 1) B 1 t

Волновые уравнения Стандартная процедура получения волновых уравнений: берем 2 а) и применяем к нему операцию rot… 3) 4)

Решение волнового уравнения: плоские волны n Найдем простейшее решение волнового уравнения. Пусть поле зависит только от одной пространственной координаты z. Тогда: , а В этом случае приходим к одномерному волновому уравнению: Для диэлектрической среды и , т. е. , тогда

Решение волнового уравнения: плоские волны Пусть Ey=0, а Тогда приходим к одномерному скалярному волновому уравнению: Очевидно, что в его решении z и t должны входить в выражение для поля Ex одинаковым образом. Поэтому решение можно представить в виде плоской скалярной волны: Здесь скорость распространения волны в среде , где r и r – относительные магнитная и диэлектрическая проницаемости среды.

Гармонические плоские волны n Если при z=0 имеется гармоническое возмущение , то получим: Это две гармонические плоские волны, которые бегут в направлениях +z и –z Мгновенное значение возмущения в некоторой точке определяется амплитудой Em волны и ее фазой Выражение для фазы волны принято записывать в форме: , где - волновое число.

Гармонические плоские волны n Геометрическое место точек, в которых фаза волны одинакова, называется волновым или фазовым фронтом Из условия изменения фазы на 2 на расстоянии в l
Структура поля плоской волны в однородной среде ,

Спасибо за внимание!
Волоконная оптика лекция1.ppt