Волны Характеристики волн Типы волн Уравнение бегущей волны

Волны Характеристики волн. Типы волн. Уравнение бегущей волны. Стоячие волны.

Волна – процесс распространения колебаний пространстве. Процесс – периодический не только во времени, но и в пространстве Механика Волна – процесс распространения колебаний в упругой среде (твёрдой, жидкой и газообразной). Если в каком либо месте упругой среды возбудить колебания её частиц, то колебание станет распространяться от частицы к частице с некоторой скоростью v. Частицы среды совершают колебания около своих положений равновесия и не переносятся волной. Продольные волны – направление колебаний вдоль направления распространения волны (любая упругая среда: твёрдая, жидкая газообразная). Поперечные волны – направление колебаний перпендикулярно направлению распространения волны: электромагнитные волны, твёрдое тело (сопротивление деформации сдвига).

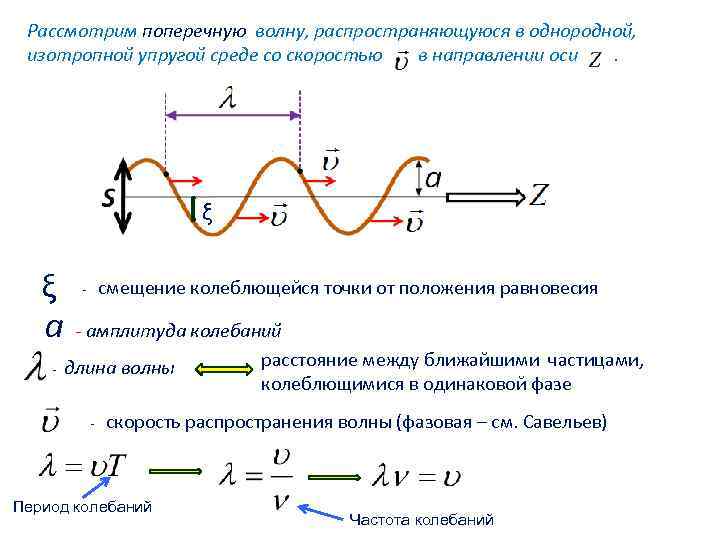
Рассмотрим поперечную волну, распространяющуюся в однородной, изотропной упругой среде со скоростью в направлении оси. ξ ξ a - смещение колеблющейся точки от положения равновесия - - амплитуда колебаний расстояние между ближайшими частицами, длина волны колеблющимися в одинаковой фазе - скорость распространения волны (фазовая – см. Савельев) Период колебаний Частота колебаний

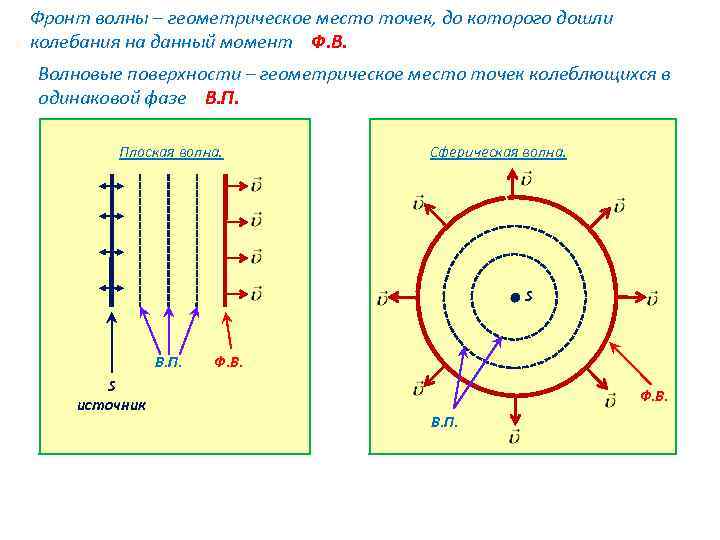
Фронт волны – геометрическое место точек, до которого дошли колебания на данный момент Ф. В. Волновые поверхности – геометрическое место точек колеблющихся в одинаковой фазе В. П. Плоская волна. Сферическая волна. S В. П. S источник Ф. В. В. П.

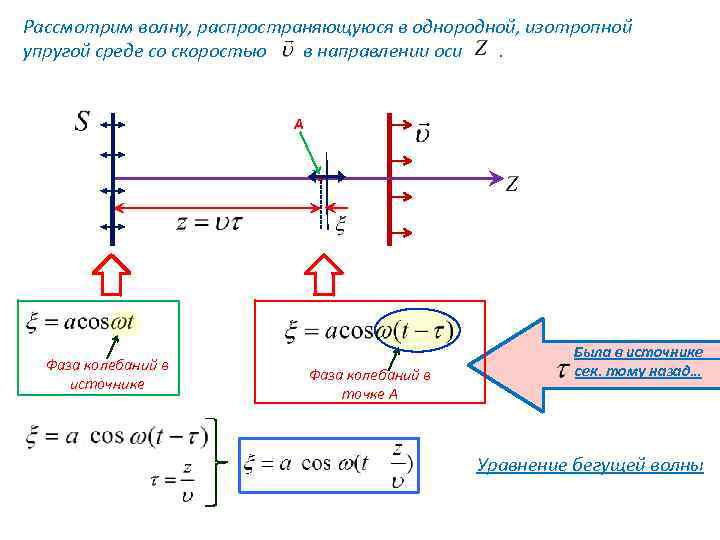
Рассмотрим волну, распространяющуюся в однородной, изотропной упругой среде со скоростью в направлении оси. А Фаза колебаний в источнике Фаза колебаний в точке А Была в источнике сек. тому назад… Уравнение бегущей волны

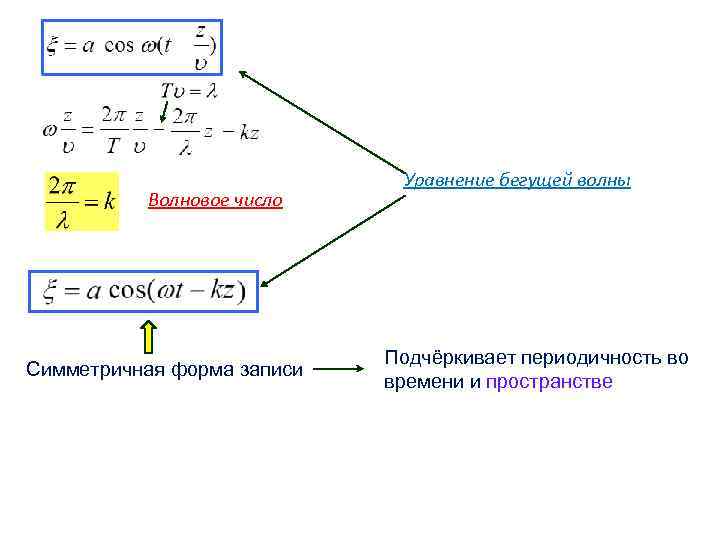
Волновое число Симметричная форма записи Уравнение бегущей волны Подчёркивает периодичность во времени и пространстве

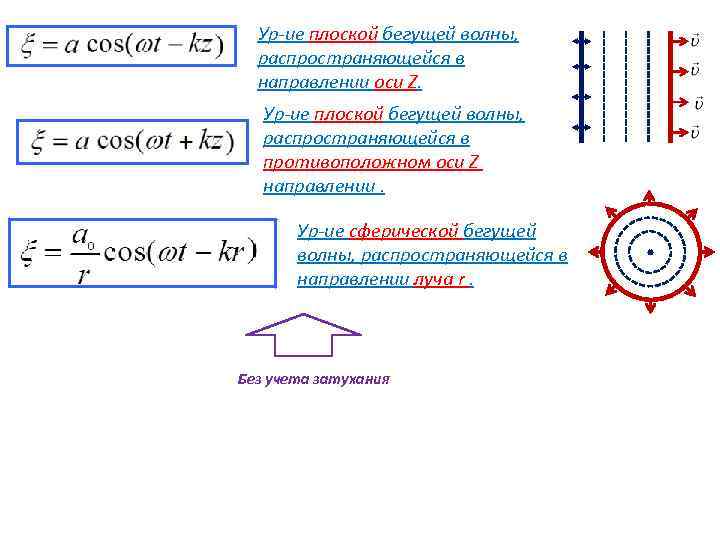
Ур-ие плоской бегущей волны, распространяющейся в направлении оси Z. Ур-ие плоской бегущей волны, распространяющейся в противоположном оси Z направлении. Ур-ие cферической бегущей волны, распространяющейся в направлении луча r. Без учета затухания

Уравнение Даламбера Дифференциальное ур-е свободных колебаний Ур-е свободных колебаний решение диф. ур-я свободных колебаний уравнение бегущей волны Найдём, решением какого диф. ур-я является ур-е бегущей волны (1) ? ?

Уравнение Даламбера уравнение бегущей волны Найдём, решением какого диф. ур-я является ур-е бегущей волны (1) Продифференцируем (1) дважды по t и по z. Частная производная Ур-е Даламбера

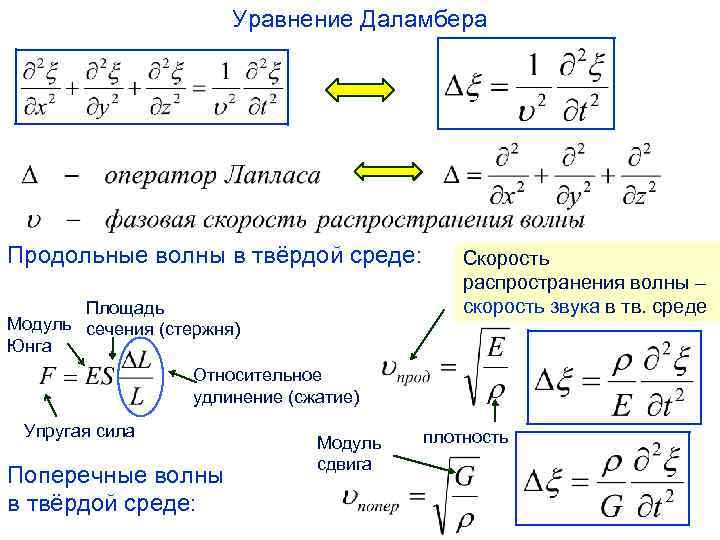
Уравнение Даламбера Продольные волны в твёрдой среде: Площадь Модуль сечения (стержня) Юнга Скорость распространения волны – скорость звука в тв. среде Относительное удлинение (сжатие) Упругая сила Поперечные волны в твёрдой среде: Модуль сдвига плотность

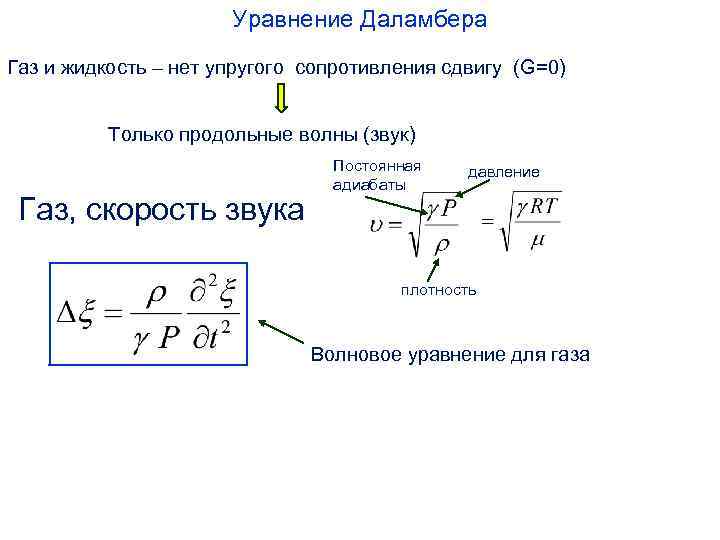
Уравнение Даламбера Газ и жидкость – нет упругого сопротивления сдвигу (G=0) Только продольные волны (звук) Газ, скорость звука Постоянная адиабаты давление плотность Волновое уравнение для газа

Энергия. Плотность энергии упругой волны. Потенциальная энергия упругой деформации - З-н Гука Потенц. энергия упругой деформации пружины Потенц. энергия упругой деформации стержня

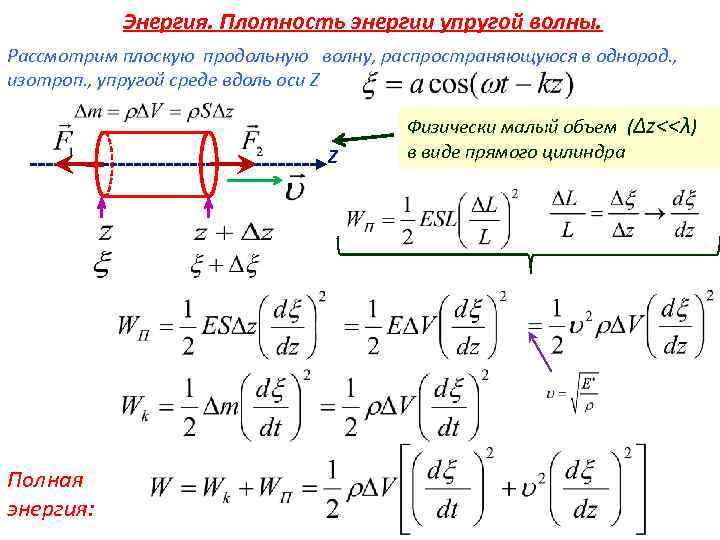
Энергия. Плотность энергии упругой волны. Рассмотрим плоскую продольную волну, распространяющуюся в однород. , изотроп. , упругой среде вдоль оси Z Z Полная энергия: Физически малый объем (Δz<<λ) в виде прямого цилиндра

Энергия. Плотность энергии упругой волны Усредненное по времени значение. Меняется по t и z (периодическая ф-ция) Средняя по времени плотность энергии волны в данной точке

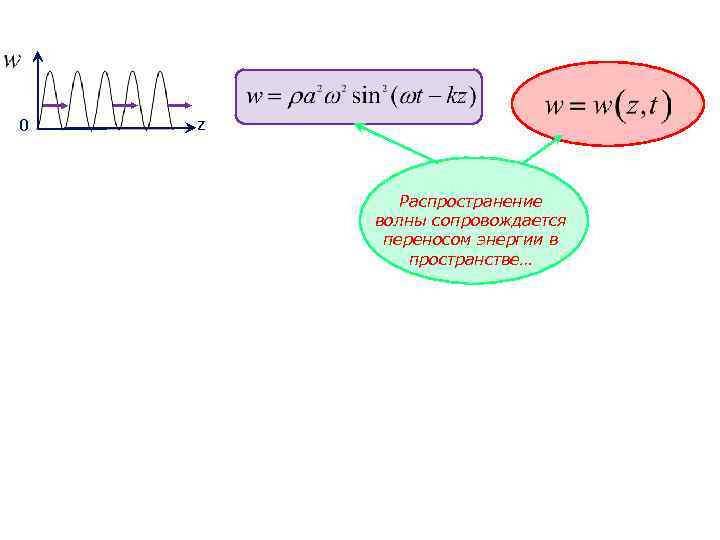
0 z Распространение волны сопровождается переносом энергии в пространстве…

Плотность потока энергии ( Вектор Умова). Поток энергии.

Зависимость амплитуды сферической волны от расстояния от источника колебаний. В случае точечного ист-ка колебаний для однородной, изотропной среды: Средний по времени поток энергии По закону сохр. энергии:

Интерференция волн Если от источника колебаний волны доходят до приёмника двумя различными путями, то приёмник будет колебаться под одновременным воздействием обеих волн будет иметь место сложение колебаний одинаковых частот. и При одинаковых направлениях слагаемых колебаний амплитуда энергия результирующего колебания: При сложении одинаково направленных колебаний равных частот энергия результирующего колебания не равна сумме энергий слагаемых колебаний, совершающихся порознь Интерференция волн – усиление или ослабление энергии результирующего колебания в зависимости от разности фаз слагаемых колебаний При сложении взаимно перпендикулярных колебаний интерференции нет, т. к. при любых энергия

Приёмник под воздействием одной первой волны совершал бы колебания, следующие уравнению: a под воздействием второй волны – уравнению Разность фаз колебаний приёмника под воздействием одного и другого колебаний: Разность расстояний , которые проходят волны от источников до приёмника, называется разностью хода волн Интерференционное усиление, согласно (1), имеет место при условии отсюда

Аналогично, для интерференционного ослабления необходимо: Таким образом: Интерференционное усиление имеет место, если разность хода лучей равна целому числу длин волн или чётному числу длин полуволн Интерференционное ослабление имеет место, если разность хода лучей равна нечётному числу длин полуволн

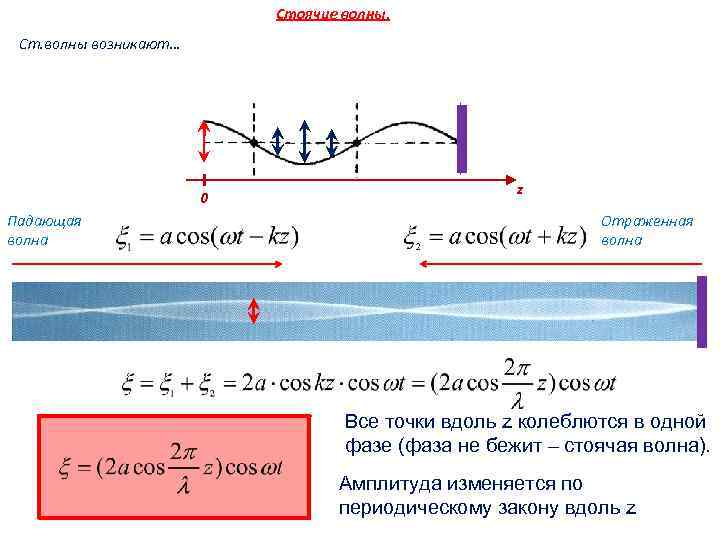
Стоячие волны. Ст. волны возникают… 0 Падающая волна z Отраженная волна Все точки вдоль z колеблются в одной фазе (фаза не бежит – стоячая волна). Амплитуда изменяется по периодическому закону вдоль z

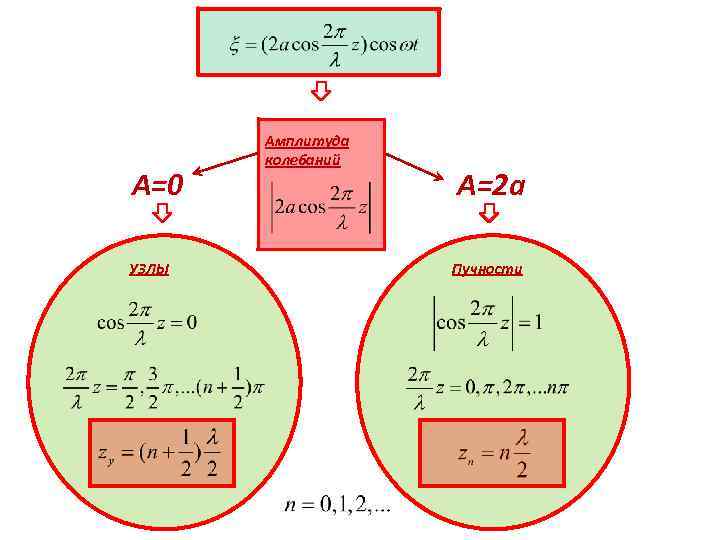
А=0 УЗЛЫ Амплитуда колебаний А=2 а Пучности