2. Волны.ppt
- Количество слайдов: 25

Волны Волнами называются процесс распространения колебаний в пространстве. Основные виды волн: - упругие (например, звуковые и сейсмические волны); - электромагнитные волны (в том числе световые и радиоволны). По характеру колебаний волны бывают: - поперечными (колебания происходят в плоскости перпендикулярной направлению распространения волны); - продольными (направление колебаний совпадает с направлением распространения волны) Характерная особенность волн - при их распространении происходит перенос энергии без переноса вещества. Упругой волной называется процесс распространения возмущения в упругой среде (там где молекулы упруго взаимодействуют друг с другом). 1

Гармоническая волна - изменение состояния среды происходит по закону синуса или косинуса. Параметры упругих гармонических волн Геометрическое место точек, до которых доходят колебания к некоторому моменту времени , называется фронтом волны или волновым фронтом. Фронт волны отделяет часть пространства, уже вовлеченную в волновой процесс, от области, в которой колебания еще не возникли. Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. По форме волновой поверхности (в простейших случаях) волны делят на: плоские, сферические, цилиндрические. 2
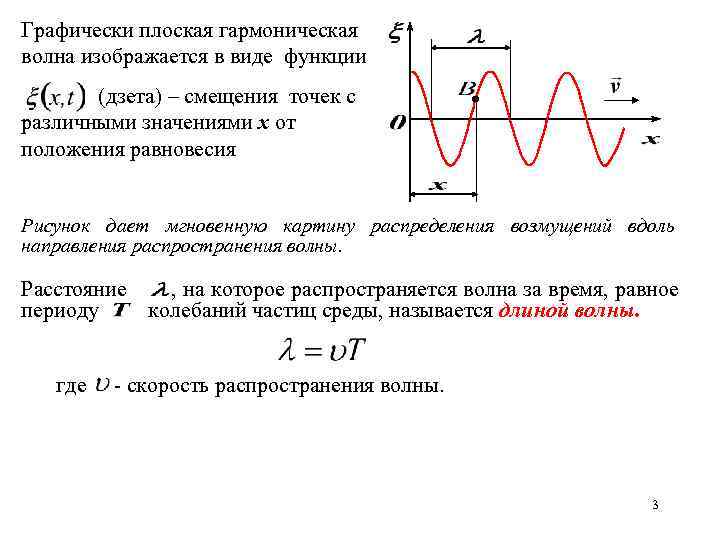
Графически плоская гармоническая волна изображается в виде функции (дзета) – смещения точек с различными значениями x от положения равновесия Рисунок дает мгновенную картину распределения возмущений вдоль направления распространения волны. Расстояние , на которое распространяется волна за время, равное периоду колебаний частиц среды, называется длиной волны. где - скорость распространения волны. 3

Уравнения плоской и сферической волн Уравнение волны – это уравнение, выражающее зависимость смещения колеблющейся частицы, участвующей в волновом процессе, от координаты и времени: Найдём вид функции в случае плоской волны Волновые поверхности будут перпендикулярны оси x Пусть колебание точки с координатой х=0 задается функцией (источник колебаний) Для того, чтобы пройти путь от плоскости x = 0 до произвольной плоскости x, волне требуется время Уравнение колебаний частиц в плоскости x 4

Уравнение плоской волны распространяющейся в направлении возрастания x Зафиксируем значение фазы Сократим на ω и продифференцируем или Скорость распространения волны есть не что иное, как скорость распространения фиксированной фазы волны. Такую скорость называют фазовой скоростью. Для синусоидальной волны скорость переноса энергии равна фазовой скорости. 5

– волновое число Подставим в уравнение плоской волны Это уравнение плоской волны, распространяющейся в сторону возрастания x Противоположное направление распространения волны 6

Уравнение сферической волны Волна от точечного источника в изотропной и однородной среде будет сферической. Точки лежащие на волновой поверхности радиуса , будут колебаться с фазой По мере расширения энергия волны будет распределяться по большей поверхности сферы. Поскольку площадь сферы 4πr 2 то плотность энергии волны будет уменьшаться как 1/r 2, следовательно амплитуда ~1/r. Следовательно, уравнение сферической волны имеет вид: Уравнение справедливо только при r. , значительно превышающих размеры источника волн. 7

Уравнения плоской и сферической волн при распространении в поглощающей среде: Групповая скорость С помощью гармонической волны нельзя передать сигнал. Сигнал должен отличаться. Быть знаком (меткой) на волне. Но тогда волна уже не будет гармонической. Сигнал (импульс) согласно теореме Фурье есть суперпозиция гармонических волн с частотами, заключёнными в интервале . Суперпозиция волн, мало отличающихся друг от друга по частоте, называется волновым пакетом или группой волн. 8

Выражение для группы волн Чтобы суперпозицию волн можно было считать группой волн нужно выполнение условия 0 Скорость, с которой перемещается центр волнового пакета (точка с максимальным значением амплитуды) называется групповой скоростью В отсутствии дисперсии скорость перемещения волнового пакета U совпадает с фазовой скорость v. 9

В диспергирующей среде v U В зависимости от знака производной быть больше или меньше фазовой групповая скорость может Максимум интенсивности приходится на центр группы волн. Поэтому скорость переноса энергии равна групповой скорости. Волновое уравнение Дифференциальное уравнение, решением которого уравнение волны, называется волновым уравнением: или является υ - фазовая скорость Показать что уравнение плоской волны удовлетворяет волновому уравнению – самостоятельно! 10
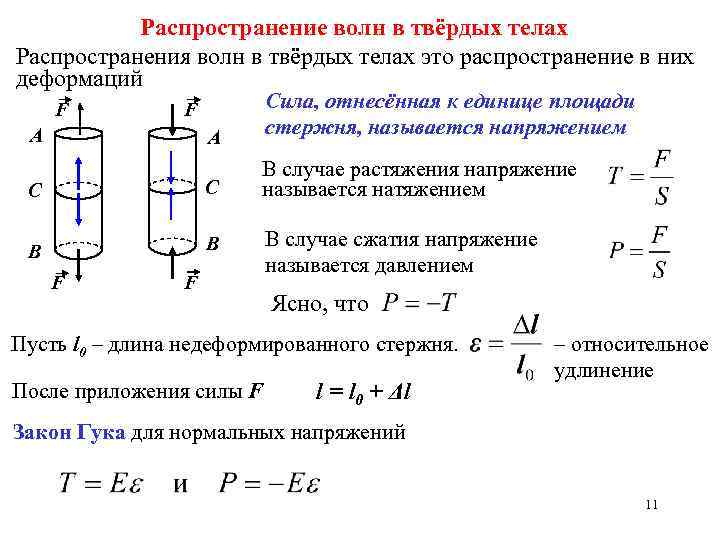
Распространение волн в твёрдых телах Распространения волн в твёрдых телах это распространение в них деформаций A Сила, отнесённая к единице площади стержня, называется напряжением C C В случае растяжения напряжение называется натяжением B B В случае сжатия напряжение называется давлением F F А F F Ясно, что Пусть l 0 – длина недеформированного стержня. После приложения силы F l = l 0 + Δl – относительное удлинение Закон Гука для нормальных напряжений 11

E – модуль Юнга. Модуль Юнга равен такому нормальному напряжению, при котором относительное удлинение равно единице, т. е. Δ l = l 0. Закон Гука справедлив только для малых деформаций. Скорость распространения упругой продольной деформации равна (волны) Для поперечных волн скорость распространения деформации равна J – модуль сдвига. Модуль сдвига равен такому тангенциальному напряжению, при котором угол сдвига оказывается равным 450 F 1 φ F 2 12

Распространение волн в газах Что выполняет роль модуля Юнга? F Рассмотрим газ в трубе: Δl l Для адиабатического процесса: Дифференцируем: или: Сравниваем (1) и (2): 13

Энергия упругой волны Энергия волны W складывается из кинетической и потенциальной Элементарный объем ΔV - настолько малый, что во всех точках этого объема скорость движения ∂ξ/∂t и деформацию ∂ξ/∂x можно считать постоянной. Плотность энергии w (энергия в единице объема) или после подстановки и дифференцирования: Среднее значение плотности энергии в каждой точке волновой среды 14

Поток энергии – количество энергии, переносимое волной через некоторую поверхность в единицу времени Ф = d. W/dt. [Ф] – Ватт. Плотность потока энергии: С другой стороны: j = wυ , j = wυ - Вектор Умова-Пойнтинга - υdt - поток энергии через единичную площадку, перпендикулярную направлению распространения волны в единицу времени. Интенсивность волны – среднее по времени значение плотности потока энергии <j> = <w>υ 15

Звуковые волны (звук) – это распространяющийся в упругой среде волновой процесс, воспринимаемый человеческим ухом. Диапазон звуковых частот – 20 Гц – 20 к. Гц. Инфразвук - волны с частотами меньше 20 Гц. Ультразвук - волны с частотами больше 20 к. Гц Акустика - учение о звуке. Скорость распространения звука различна в различных средах. Скорость звука в газах: Скорость звука в жидкости: где - молярная газовая постоянная, - термодинамическая температура, - молярная масса. - объемный модуль упругости жидкости, - плотность жидкости

Эффект Доплера состоит в том, что испускаемая регистрируемая частоты волны различаются, если источник приемник движутся относительно друга. Скорости движения источника и приемника относительно среды, которой распространяется волна, обозначим соответственно и и и в. Скорости положительны, если источник и приемник сближаются и отрицательны, если удаляются. Скорость распространения волны – υ. Частота колебаний источника равна. Если же источник или приемник, или оба движутся относительно среды, в которой распространяется волна, то частота колебаний , воспринимаемых приемником, оказывается отличной от частоты источника: . Это отличие определяется формулой: где и - проекции скоростей приемника и источника на ось x.

Электромагнитные волны Существование электромагнитного поля следует из уравнений Максвелла. Рассмотрим однородную нейтральную непроводящую среду, например, для простоты, вакуум: Дифференциальные уравнения Максвелла для рассматриваемой среды: Из этих уравнений путем несложных преобразований можно получить следующую пару уравнений: Это волновые уравнения для полей и 18

Сравнивая с волновым уравнением: В вакууме скорость электромагнитной волны равна скорости света. Скорость света в среде меньше: где Электромагнитная волна является строго поперечной волной, векторы и перпендикулярны к вектору скорости волны, т. е. к направлению ее распространения. Векторы , и , в том порядке, в котором они записаны, образуют правовинтовую ортогональную тройку векторов. В электромагнитной волне векторы и всегда колеблются в одинаковых фазах 19

Мгновенные значения этих векторов в любой точке пространства связаны соотношением Пусть электромагнитная волна будет строго монохроматической и распространяется в направлении x. Этим уравнениям удовлетворяют плоские линейно поляризованные монохроматические волны 20
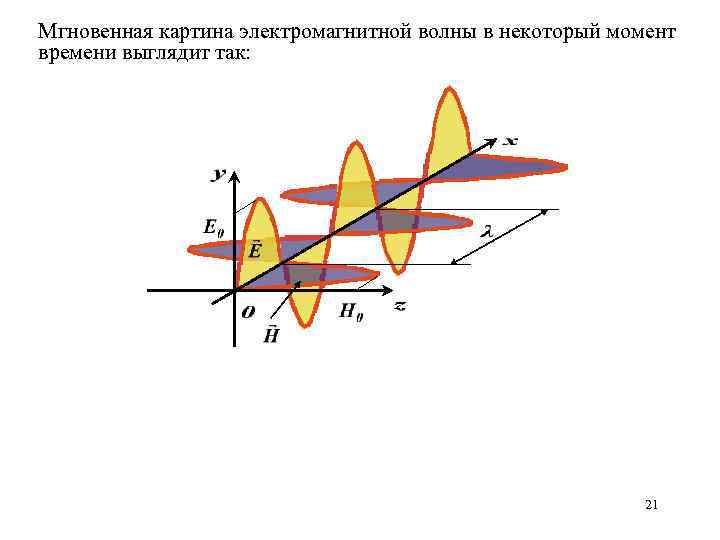
Мгновенная картина электромагнитной волны в некоторый момент времени выглядит так: 21

Энергия электромагнитной волны Электромагнитные волны переносят в пространстве энергию. Объемная плотность энергии электромагнитной волны складывается из объемных плотностей энергии электрического и магнитного полей: Если учесть связь между Е и Н, то Поскольку , то Умножив полученное выражение для w на скорость волны υ , получим модуль плотности потока энергии: 22

и взаимно перпендикулярны Поэтому направление вектора совпадает с направлением переноса энергии, а модуль этого вектора равен Вектор называется вектором Пойнтинга Для бегущей гармонической электромагнитной волны плотность энергии равна: или Плотность потока энергии: Окончательно запишем: или 23

Интенсивность электромагнитной волны Для периодической волны более информативным, чем мгновенное значение вектора Пойнтинга, является значение, усредненное по периоду волны. Это интенсивность электромагнитной волны I = <S> При усреднении по периоду среднее значение квадрата косинуса равно ½ , следовательно, окончательно получится: или Импульс электромагнитной волны Плотность импульса (импульс отнесенный к единице объема): 24

25
2. Волны.ppt